【LeetCode-329】矩阵中的最长递增路径

问题

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例

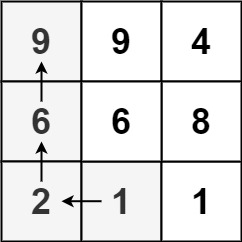
输入： matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出： 4
解释： 最长递增路径为 [1, 2, 6, 9]。

解答

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        memo.assign(m, vector<int>(n));
        int res = 0;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                res = max(res, dfs(matrix, i, j));
        return res;
    }
private:
    vector<vector<int>> memo;
    int dx[4]{-1, 1, 0, 0};
    int dy[4]{0, 0, 1, -1};
    int dfs(vector<vector<int>>& matrix, int x, int y) {
        if (memo[x][y]) return memo[x][y];
        int ans = 1;
        for (int i = 0; i < 4; i++) {
            int nx = dx[i] + x, ny = dy[i] + y;
            if (nx < 0 || nx == matrix.size() || ny < 0 || ny == matrix[0].size()) continue; // 保证不出边界
            if (matrix[x][y] <= matrix[nx][ny]) continue; // 保证严格递增
            ans = max(ans, dfs(matrix, nx, ny) + 1);
        }
        return memo[x][y] = ans;
    }
};

重点思路

经典的DFS问题，需要注意的是要使用记忆化搜索，可以把时间复杂度降低到\(O(mn)\)，m和n为矩形的长宽。