【LeetCode-847】访问所有节点的最短路径

问题

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

提示：

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] 不包含 i
• 如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
• 输入的图总是连通图

示例

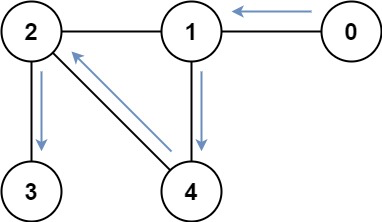
输入： graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出： 4
解释： 一种可能的路径为 [0,1,4,2,3]

解答

class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<tuple<int, int, int>> q; // idx, state, dist
        vector<vector<bool>> vis(n, vector<bool>(1 << n));
        for (int i = 0; i < n; i++) {
            q.emplace(i, 1 << i, 0);
            vis[i][1 << i] = true;
        }
        while (!q.empty()) {
            auto [idx, state, dist] = q.front();
            q.pop();
            if (state == (1 << n) - 1) return dist;
            for (int v : graph[idx]) {
                int cur_state = state | (1 << v);
                if (vis[v][cur_state]) continue;
                q.emplace(v, cur_state, dist + 1);
                vis[v][cur_state] = true;
            }
        }
        return 0;
    }
};

重点思路

本题知识点：

• 多源BFS：由于每条边等权，先处理哪个点都一样，所以可以使用多源BFS；
• 状态压缩：可以使用0和1表示是否经过某一个节点，本题规定最多12个节点，所以可以使用一个int类型的整数，取低12位表示遍历状态。

假设有8个节点，当表示状态的整数为\((...0011111111)_2\)时，表示此时已经遍历了所有节点，多源BFS保证当前一定是遍历完成的最短距离，直接输出当前距离即可。为保证每个“状态”（两个约束，当前节点的idx与对应的遍历状态state）只经过一次，使用二维数组存储已遍历状态。有点类似遍历二维数组时存储的横纵坐标，本质是一样的，保证不会经过重复“状态”。