【推荐算法】AUC的计算方法

AUC是衡量二分类模型优劣的一种评价指标，有两种等价定义：

• 面积定义：ROC曲线下围成的面积
• 物理定义：模型预测的正例排在负例前面的概率

面积定义

AUC通常指ROC曲线下的面积（Area Under the ROC Curve）。其中，ROC（Receiver Operating Characteristic curve）的横轴为FPR，纵轴为TPR。

\(\text{FPR}=\frac{\text{FP}}{\text{N}}\)，指假阳性样本占负样本的比例；
\(\text{TPR}=\frac{\text{TP}}{\text{T}}\)，指真阳性样本占正样本的比例，也称作召回率。

模型预估的值为该样本标签为1的概率，我们通过设置不同的阈值来决定该样本为正例还是负例。阈值变化，FPR和TPR也随之发生变化，遍历所有可能的阈值，我们能得到ROC曲线。在作图时，我们可以只考虑会导致FPR和TPR变化的阈值，具体来说，我们将阈值从1逐步调整到0，取值范围为所有样本的每个预测概率，此时FPR和TPR都会从0逐步增加到1，具体如下图：

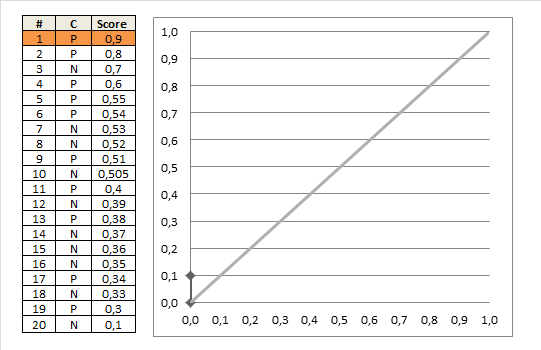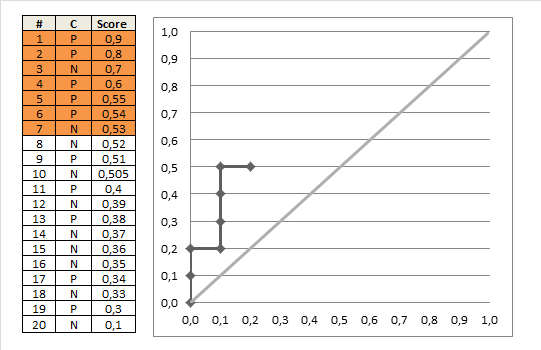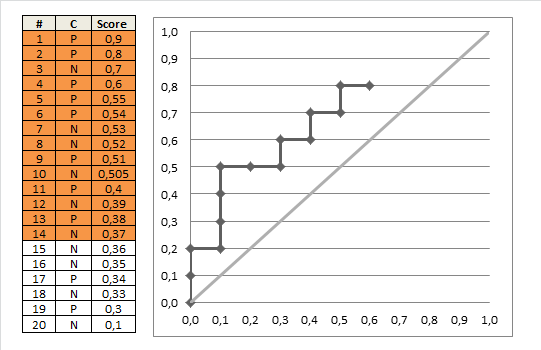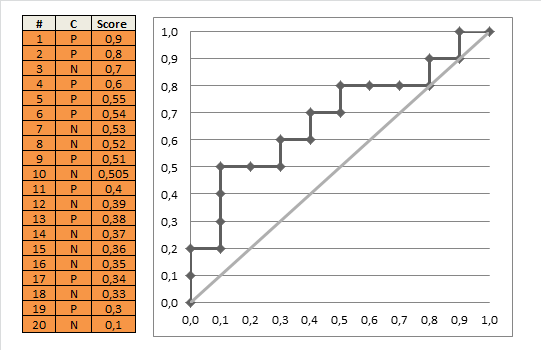
依据以上分析，按照面积计算AUC的代码为：

double get_auc(vector<double>& prob, vector<int>& label) {
    int n = label.size(), pos = 0;
    vector<pair<double, int>> pl;
    for (int i = 0; i < n; i++) {
        pos += label[i];
        pl.emplace_back(prob[i], label[i]);
    }
    sort(pl.begin(), pl.end(), [&](auto a, auto b){return a.first > b.first;});
    double auc = 0;
    for (int left = 0, right = 0, pre_tp = 0; right < n; left = right) {
        int delta_fp = 0, delta_tp = 0;
        while (right < n && pl[right].first == pl[left].first)
            pl[right++].second ? delta_tp++ : delta_fp++;
        auc += (2 * pre_tp + delta_tp) * delta_fp / 2.;
        pre_tp += delta_tp;
    }
    return auc / (pos * (n - pos));
}

物理定义

除了上述由TPR和FPR定义的AUC，其还有更直观的物理意义：模型预测正样本为1的概率比预测负样本为1的概率高的概率。对于此概率，我们有两种计算方法：

1. 最直观的方法，统计出所有“正样本-负样本”二元组，其中正样本概率大于负样本的+1，概率相同的+0.5，最后除以二元组数量；
2. 上面方法的时间复杂度较高，可以先对概率排序，通过正样本的rank（越小rank越大）来计算当前正样本的概率大于多少负样本，以此可以得到正样本概率大于负样本的总数。后续讨论统一使用该方法。

首先，简化一下原问题，不考虑有相同概率出现，此时AUC的计算公式为：

\[\text{AUC}=\frac{\sum_{i\in positiveClass}rank_i-\frac{T \times (T+1)}{2}}{T\times N} \tag{1} \]

对于有相同概率的情况，需要将概率相同的所有rank作平均（具体证明参考该论文），代码如下：

double get_auc(vector<double>& prob, vector<int>& label) {
    int n = label.size(), pos = 0;
    vector<pair<double, int>> pl;
    for (int i = 0; i < n; i++) {
        pos += label[i];
        pl.emplace_back(prob[i], label[i]);
    }
    sort(pl.begin(), pl.end());
    double pos_sum = 0;
    for (int left = 0, right = 0; right < n; left = right) {
        double sum = 0, cnt = 0;
        while (right < n && pl[right].first == pl[left].first) {
            cnt += pl[right++].second;
            sum += right;
        }
        pos_sum += sum * cnt / (right - left);
    }
    return (pos_sum - (pos * (pos + 1) / 2)) / (pos * (n - pos));
}

两种定义的联系

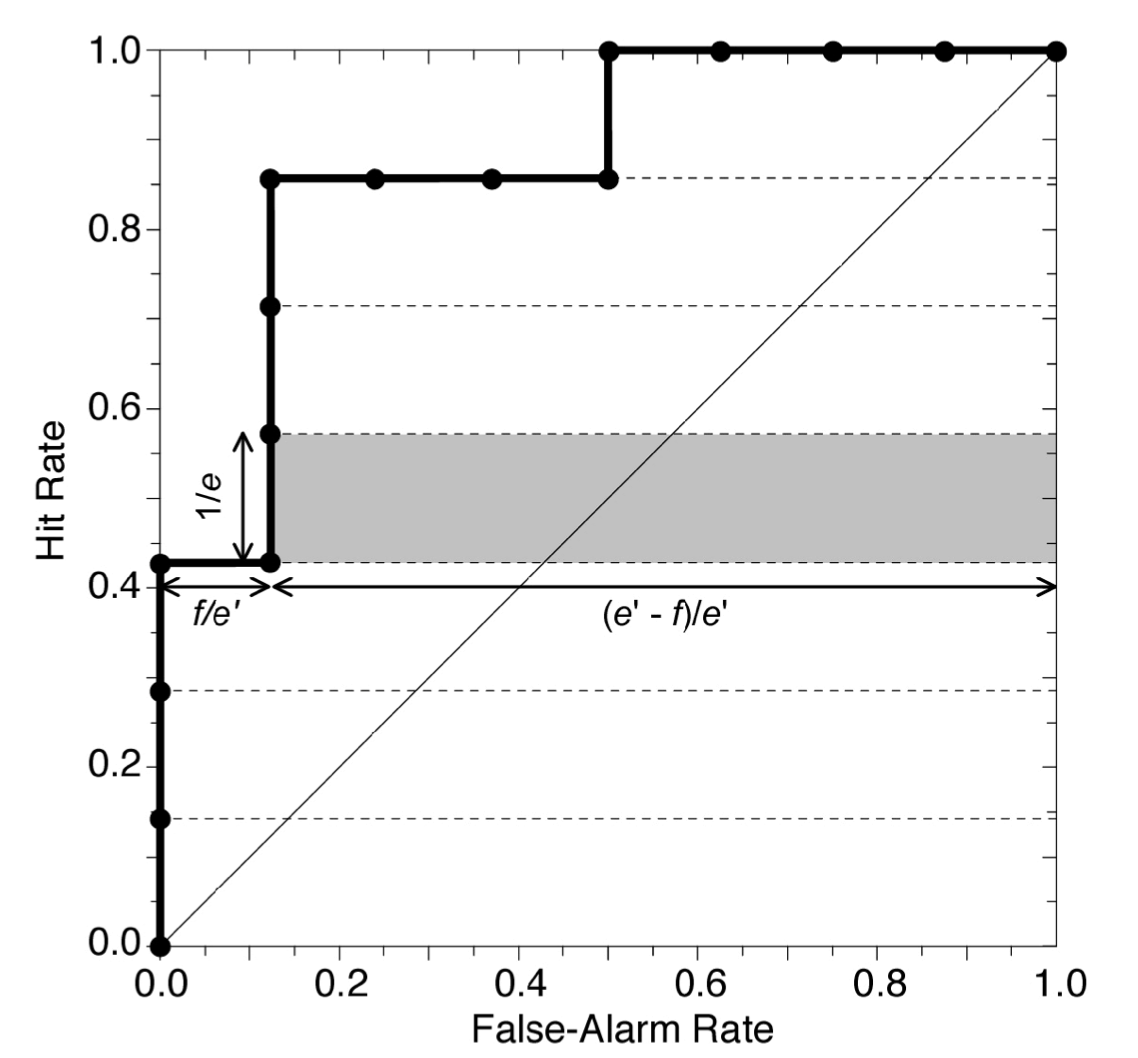
图中，\(e\)为正样本数量，\(e^{\prime}\)为负样本数量。从图片可知，只有当TPR上升时，才会有新增面积。此时新增面积为，

\[\text { area gained }=\frac{\left(e^{\prime}-f\right)}{e^{\prime} e} \]

其中\(f\)表示当前点，负例被预测成正例的数量。所以整个ROC曲线下面的面积为，

\[\text{AUC}=\frac{1}{e^{\prime} e} \sum_{i=1}^{e}\left(e^{\prime}-f_{i}\right)=1-\frac{1}{e^{\prime} e} \sum_{i=1}^{e} f_{i} \]

其中，

\[\sum_{i=1}^{e} f_{i}=\sum_{i=1}^{e}\left(r_{i}-i\right)=\sum_{i=1}^{e} r_{i}-\frac{e(e+1)}{2} \]

这里的\(r_i\)为由大到小的排序rank，将其变为从小到大的rank排序即可得到公式（1）。