【LeetCode-363】矩形区域不超过 K 的最大数值和

问题

给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

示例

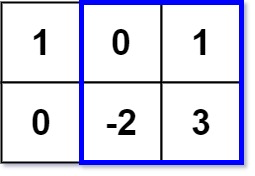
输入： matrix = [[1,0,1],[0,-2,3]], k = 2
输出： 2
解释： 蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。

解答1：前缀和+暴力

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size(), res = INT_MIN;
        int preSum[m + 1][n + 1]; bzero(preSum, sizeof preSum);
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                for (int p = i; p <= m; p++) {
                    for (int q = j; q <= n; q++) {
                        int ans = preSum[p][q] - preSum[i - 1][q] - preSum[p][j - 1] + preSum[i - 1][j - 1];
                        if (ans <= k) res = max(res, ans);
                    }
                }
            }
        }
        return res;
    }
};

重点思路

本题需要求一个矩形内所有元素的和，首先要想到使用前缀和。然后使用暴力进行遍历即可，时间复杂度为\(O(m^2n^2)\)。

解答2：前缀和+二分

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size(), res = INT_MIN;
        int preSum[m + 1][n + 1]; bzero(preSum, sizeof preSum);
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
        for (int t = 1; t <= m; t++) { // t为top
            for (int b = t; b <= m; b++) { // b为bottom
                set<int> st; // 保证内部元素的有序性
                for (int r = 0; r <= n; r++) { // r为矩阵的右边界
                    int right = preSum[b][r] - preSum[t - 1][r]; // right为当前b和t下，0～r部分矩阵的和
                    auto left = st.lower_bound(right - k); // 二分查找
                    if (left != st.end()) {
                        int ans = right - *left;
                        res = max(res, ans);
                    }
                    st.insert(right);
                }
            }
        }
        return res;
    }
};

重点思路

先看一维问题。设我们要找right - left <= k，所以left >= right - k，所以我们只需要二分查找大于等于right - k的数即可。

我们可以从一维问题拓展到二维问题上。我们固定矩阵的“上”、“下”、“右”三条边，然后二分查找“左”这条边。时间复杂度为\(O(m^2nlog(n))\)

解答2：前缀和+二分（优化）

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size(), res = INT_MIN;
        int preSum[m + 1][n + 1]; bzero(preSum, sizeof preSum);
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
        bool flag = 1; // flag = 1表示不交换行列顺序
        if (m > n) { // 行比列多时，交换行列
            swap(m, n);
            flag = 0;
        }
        for (int t = 1; t <= m; t++) {
            for (int b = t; b <= m; b++) {
                set<int> st;
                for (int r = 0; r <= n; r++) {
                    int right = flag ? preSum[b][r] - preSum[t - 1][r] : preSum[r][b] - preSum[r][t - 1]; // 行列的对应操作
                    auto left = st.lower_bound(right - k);
                    if (left != st.end()) {
                        int ans = right - *left;
                        res = max(res, ans);
                    }
                    st.insert(right);
                }
            }
        }
        return res;
    }
};

重点思路

我们应尽可能利用二分性质，对行列中较长的那一部分使用二分。时间复杂度为\(O(min(m, n)^2max(m, n)log(max(m, n)))\)。