【C++】Manacher算法

Manacher算法可以在O(n)的时间复杂度解决最长回文串问题。

字符串预处理

为了避免讨论奇偶性，首先对原始字符串进行预处理，也就是在每个字符间隙加上#，即将aab变为#a#a#b#。当指向#时，代表回文串长度为偶数，否则为奇数。

string t = "#";
for (char c : s) { // 输入字符串为s
    t += c;
    t += "#";
}

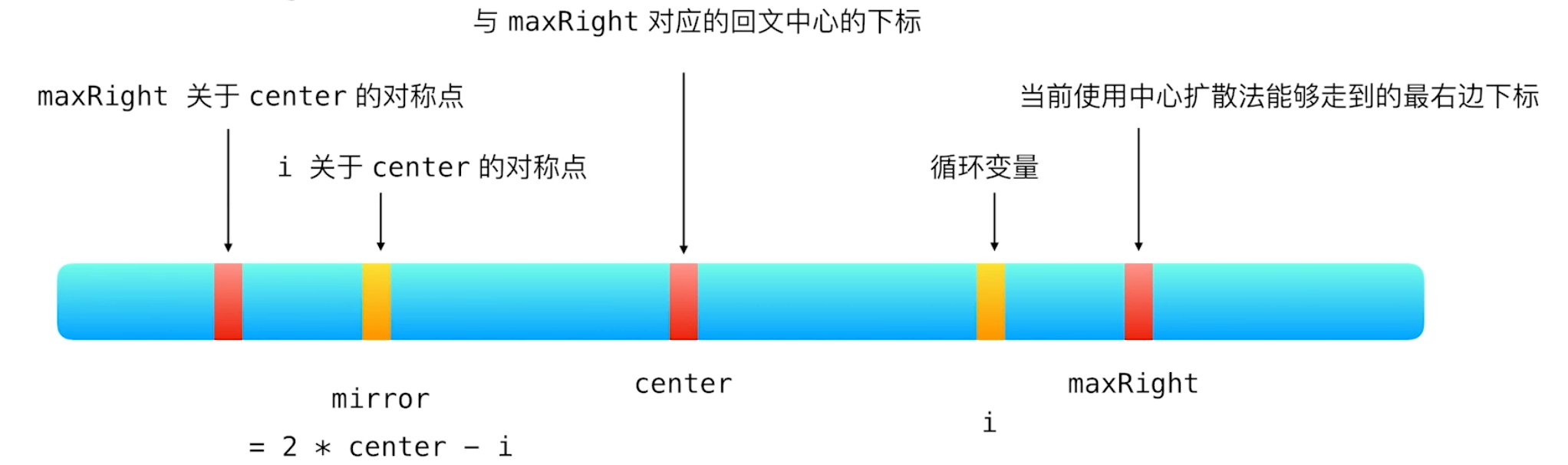
获取以当前位置为回文串中心的最长回文串长度

我们使用一个dp数组记录以每个位置为中心的最长回文串长度。从图中可以看出dp[i]与dp[mirror]有很大的关系。实际上，我们需要讨论dp[mirror]与maxRight - i的大小关系，从而确定dp[i]的取值。在此过程中，需要注意center和maxRight的更新。

dp[mirror] < maxRight - i

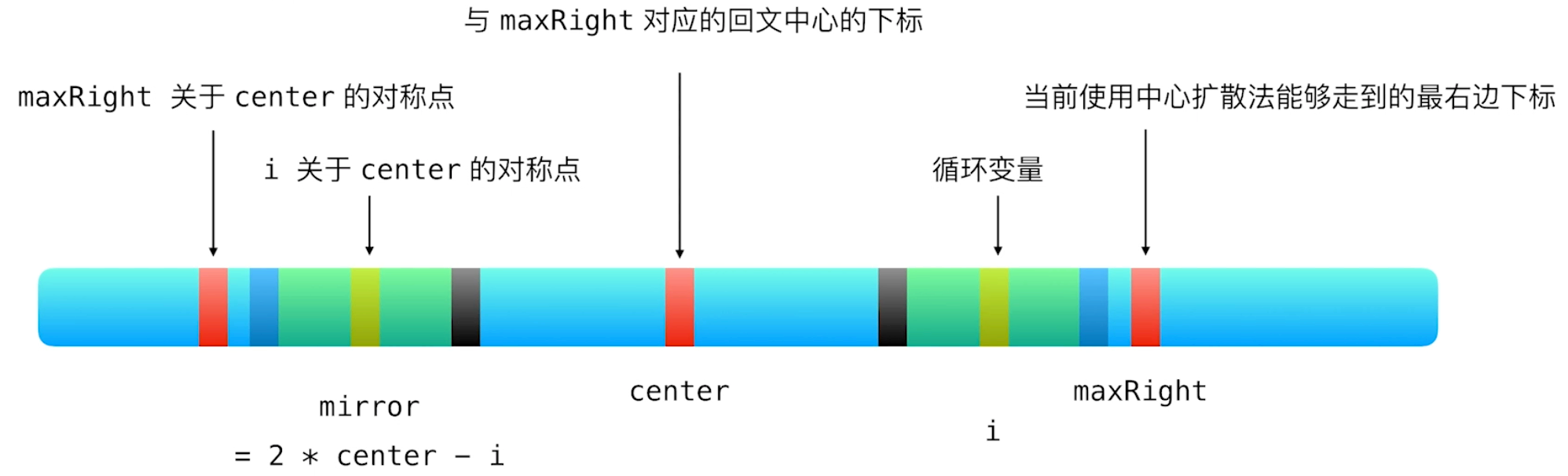
此时，mirror处对应的最长回文串被包含在center处对应的最长回文串中，根据center处的回文串对称性可以作出上图。易得dp[i] = dp[mirror]。

dp[mirror] == maxRight - i

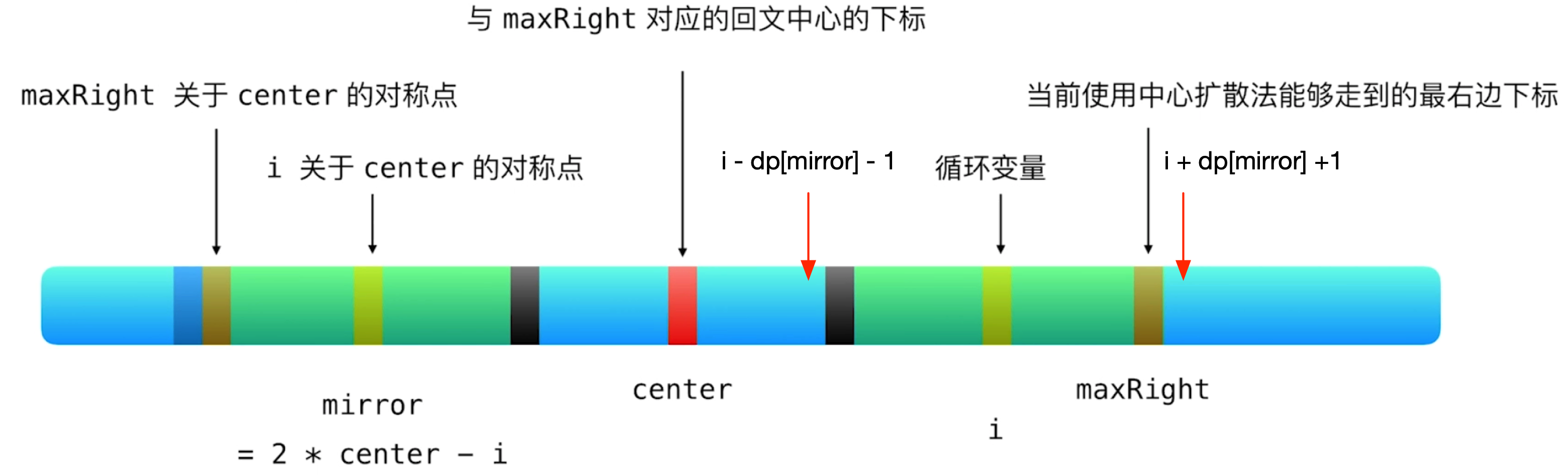
此时，我们需要继续判断红箭头所指位置是否可以继续中心扩展。

dp[mirror] > maxRight - i

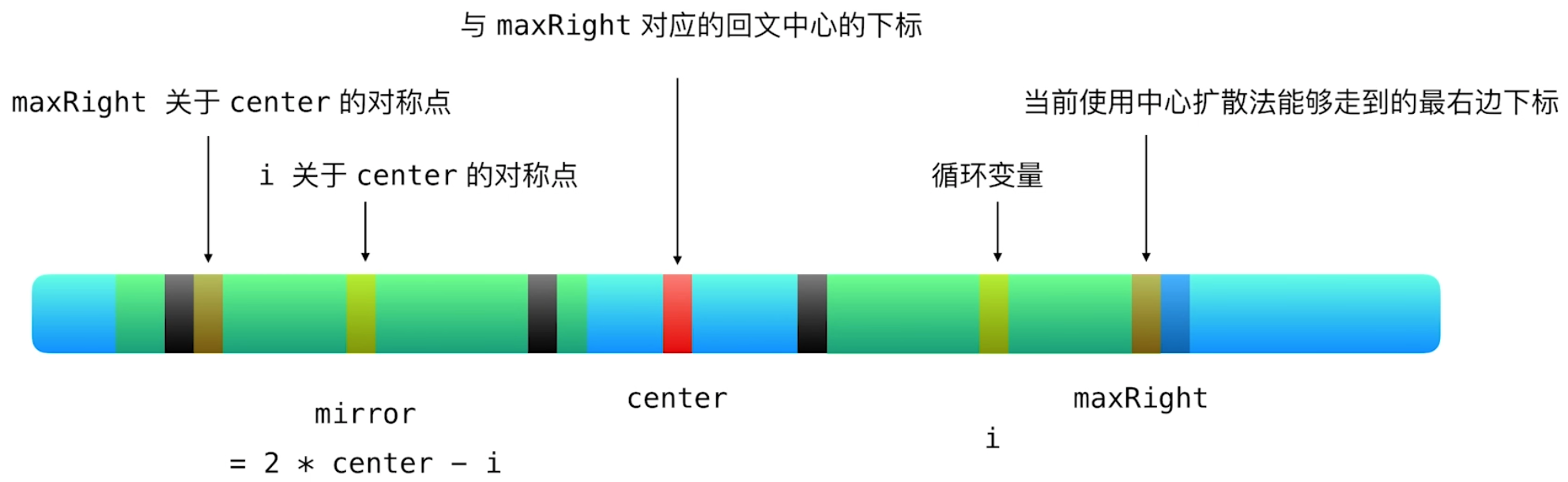
由于存在maxRight，根据mirror与center的对称性，此时做中心扩展必定不会成功（否则以center为中心的最长回文串一定会更长），可以得到dp[i] = maxRight - i。

获取原始字符串中最长回文串对应的起始位置以及长度

分别用maxLen与begin表示。举个例子，原始字符串为aaba，预处理后为#a#a#b#a#。此时最长回文串为aba，对应的dp[5] = 3（臂长为3，对应#a#），正好为aba的长度。起始位置为1，而i - maxLen为2，相减后剩余字符串为#a，恢复到原始字符串中需要除以2。

if (dp[i] > maxLen) {
    maxLen = dp[i];
    begin = (i - maxLen) / 2;
}

代码

将上述讨论统一起来，可以得到：

class Solution {
public:
    string longestPalindrome(string s) {
        string t = "#";
        for (char c : s) {
            t += c;
            t += "#";
        }
        int maxRight = 0, center = 0; // 当前回文串最远能到达的的右边界和其中心
        int maxLen = 1, start = 0; // 原字符串中最长回文串对应的起始位置和长度
        int n = t.size();
        int dp[n];// 存储臂长
        for (int i = 0; i < n; i++) {
            dp[i] = i < maxRight ? min(dp[2 * center - i], maxRight - i) : 0;
            if (i + dp[i] < maxRight) continue;
            int left = i - dp[i], right = i + dp[i]; // 初始化中心扩展位置
            while (--left >= 0 && ++right < n && t[left] == t[right]) dp[i]++; // 中心扩展
            maxRight = i + dp[i], center = i;
            if (dp[i] > maxLen) { // 更新原始字符串中的起始位置和长度
                maxLen = dp[i];
                start = (i - maxLen) / 2;
            }
        }
        return s.substr(start, maxLen);
    }
};

不修改原始字符串的代码

模拟包含#的情况。

class Solution {
public:
    string longestPalindrome(string s) {
        int maxRight = 0, center = 0;
        int maxLen = 1, start = 0;
        int n = s.size() * 2 + 1;
        int dp[n];
        for (int i = 0; i < n; i++) {
            dp[i] = i < maxRight ? min(dp[2 * center - i], maxRight-i) : 0;
            if (dp[i] + i < maxRight) continue;
            int left = i - dp[i], right = i + dp[i];
            while(--left >= 0 && ++right < n && (left % 2 == 0 || s[left / 2] == s[right / 2])) dp[i]++;
            maxRight = i + dp[i], center = i;
            if (dp[i] > maxLen){
                maxLen = dp[i];
                start = (i - maxLen) / 2;
            }
        }
        return s.substr(start, maxLen);
    }
};