【C++】KMP算法

KMP算法用于解决字符串匹配问题，时间复杂度为O(m + n)。设s为待匹配字符串，'p'为m为模版字符串。'm'为s的长度，n为p的长度）

运用前后缀性质减少重复比较

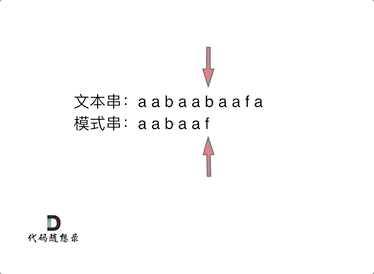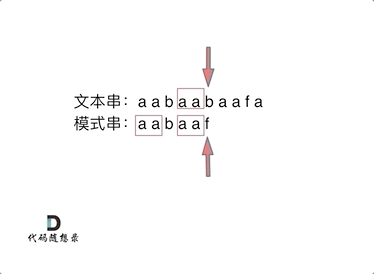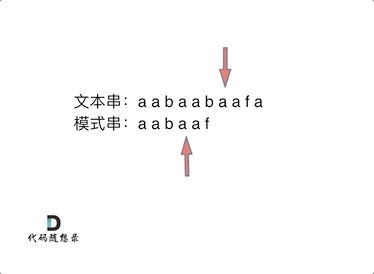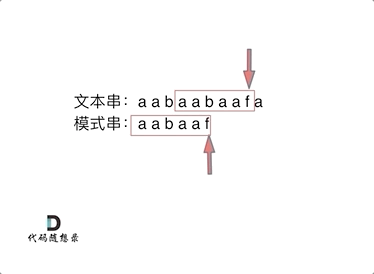
从上图可以看出，当b与f失配时，与朴素暴力解法中直接将p后移一位继续比较不同，KMP方法利用p中存在的最长公共前后缀aa省略了重复的比较。因为前面已经成功匹配了后缀aa，而p中存在相同的前后缀aa，所以就相当于已经成功匹配了前缀aa，那么接下来只需要继续匹配前缀aa后面的字符即可。设j为指向p中字符的指针，设next[]对应p中每个字符的转移位置，设[0, j - 1]对应的字符串的最长前后缀长度为k，则我们需要将指针转移到k的位置。上述操作可表示为j = next[j - 1]。

构建next转移数组

设当前位置为j，next[j]就是[0, j]对应字符串的最长公共前后缀长度。使用双指针，时间复杂度为O(n)。

int next[n];
for (int i = 1, j = next[0] = 0; i < n; i++) {
    while (j && p[i] != p[j]) j = next[j - 1]; // 因为角标存在j-1，所以必须设定j>0
    if (p[i] == p[j]) j++; // i为前缀最后角标，j为后缀最后角标
    next[i] = j;
}

使用next进行字符串匹配

得到p中每个字符对应的转移位置后，我们可以以O(m + n)的时间复杂度对整个s进行匹配。

vector<int> res;
for (int i = 0, j = 0; i < m; i++) {
    while (j && s[i] != p[j]) j = next[j - 1]; // 转移到下一个公共前后缀继续匹配
    if (s[i] == p[j]) j++;
    if (j == n) { // 到达p末尾说明整段匹配成功
        res.push_back(i - n + 1);
        j = next[j - 1]; // 匹配成功后，当作此次匹配失败，继续后一次匹配
    }
    return res;
}

整体代码

class Solution {
public:
    vector<int> strStr(string s, string p) {
        int m = s.size(), n = p.size();
        if (n == 0) return {0};
        vector<int> res;
        int next[n];
        for (int i = 1, j = next[0] = 0; i < n; i++) {
            while (j && p[i] != p[j]) j = next[j - 1];
            if (p[i] == p[j]) j++;
            next[i] = j;
        }
        for (int i = 0, j = 0; i < m; i++) {
            while (j && s[i] != p[j]) j = next[j - 1];
            if (s[i] == p[j]) j++;
            if (j == n) {
                res.push_back(i - n + 1);
                j = next[j - 1];
            }
        }
        return res;
    }
};