【LeetCode-84】柱状图中最大的矩形

问题

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

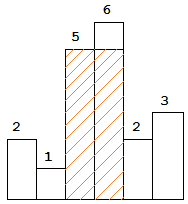
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

解答1：暴力（中心扩散）

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size(), res = 0;
        for (int i = 0; i < n; i++) {
            int left = i, right = i;
            while (left >= 0 && heights[i] <= heights[left]) left--; // 找到左边第一个比i处小的，坐标为left
            while (right < n && heights[i] <= heights[right]) right++; // 找到右边第一个比i处大的，坐标为right
            res = max(res, (right - left - 1) * heights[i]); // (left, right)开区间内满足要求
        }
        return res;
    }
};

重点思路

注意扩散的起始位置，注意左右的开闭区间。

解答2：单调栈

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.push_back(0);
        heights.insert(heights.begin(), 0);
        stack<int> s; // 递增
        int res = 0, n = heights.size();
        for (int i = 0; i < n; i++) {
            while (!s.empty() && heights[s.top()] > heights[i]) {
                // ------ 单调栈操作部分
                int cur = s.top(); s.pop();
                int l = s.top(), r = i;
                int w = r - l - 1;
                res = max(res, w * heights[cur]);
                // ------
            }
            s.push(i);
        }
        return res;
    }
};

重点思路

本题和【LeetCode-42】接雨水很类似，区别在于，接雨水要求的是当前位置的上一个和下一个比它高的位置，而本题要求的是当前位置的上一个和下一个比它低的位置。要特别注意边界条件以及不同题目对应的的不同单调栈操作。