【剑指Offer-68-II】二叉树的最近公共祖先

问题

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

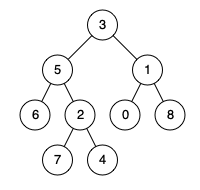
示例

输入： root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出： 3
解释： 节点 5 和节点 1 的最近公共祖先是节点 3。

解答1：求出路径（回溯）

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* res;
        findTrace(root, p, traceP); flag = 1;
        findTrace(root, q, traceQ);
        int n = min(traceP.size(), traceQ.size());
        for (int i = 0; i < n; i++)
            if (traceP[i] == traceQ[i]) res = traceP[i];
        return res;
    }
private:
    vector<TreeNode*> traceP, traceQ;
    bool flag = 1; // 剪枝
    void findTrace(TreeNode* root, TreeNode* p, vector<TreeNode*>& trace) {
        if (!root || !flag) return;
        trace.push_back(root);
        if (root == p) flag = 0;
        findTrace(root->left, p, trace);
        findTrace(root->right, p, trace);
        if (flag) trace.pop_back();
    }
};

重点思路

使用回溯法求出两个节点的路径。再从这两条路径中找到最近公共祖先。

解答2：递归

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root || root == q || root == p) return root; // 对应1
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (!left) return right; // p、q在右子树，祖先在右子树，对应4
        if (!right) return left; // p、q在左子树，祖先在左子树，对应3
        else return root; // p、q在两边，祖先为根节点，对应2
    }
};

重点思路

递归问题，需要首先分析输入、输出、终止条件。

二叉树当前节点是公共祖先时一共有两种情况：

1. root = p或者root = q；
2. p和q在root的两侧子树中。

找到子树时，直接返回root。

二叉树当前节点不是公共祖先时一共有两种情况：
3. 公共祖先在当前节点的左子树中；
4. 公共祖先在当前节点的右子树中。