【剑指Offer-68-I】二叉搜索树的最近公共祖先

问题

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

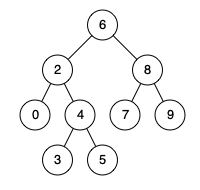
示例

输入： root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出： 2
解释： 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

解答1：迭代

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (q->val < p->val) swap(q, p); // 保证p值小于等于q值，方便后面的比较
        while (1) { // 二叉树的两个节点必定存在公共祖先
            if (root->val > q->val) root = root->left;
            else if (root->val < p->val) root = root->right;
            else break;
        }
        return root;
    }
};

重点思路

根据二叉搜索树的定义。根节点值大于左子树的任意节点值，小于右子树的任意节点值。所以当大于这两个值的时候，往左子树移动；小于这两个值的时候，往右子树移动；其余任何情况，都直接输出节点。

解答2：递归

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val)
            return lowestCommonAncestor(root->left, p, q);
        if (root->val < p->val && root->val < q->val)
            return lowestCommonAncestor(root->right, p, q);
        return root;
    }
};

重点思路

递归的输入输出为树节点，终止条件为已找到公共祖先，找到公共祖先的要求为不比两个节点都大并且不比两个节点都小。