【剑指Offer-62】圆圈中最后剩下的数字

问题

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例

输入： n = 5, m = 3
输出： 3

解答1：递归

class Solution {
public:
    int lastRemaining(int n, int m) {
        if (n == 1) return 0;
        return (lastRemaining(n - 1, m) + m) % n;
    }
};

重点思路

这道题就是著名的约瑟夫环问题。直接套个链表开始模拟肯定是最容易想到的，但是这道题会超时。其实这道题可以用动态规划或者递归来做。我们设长度为n，每次移动m的最终结果为f(n, m)，那么就需要找到f(n, m)与f(n - 1, m)的关系。下图很好地说明了这一关系，其中，C为n - 1时去掉的元素。

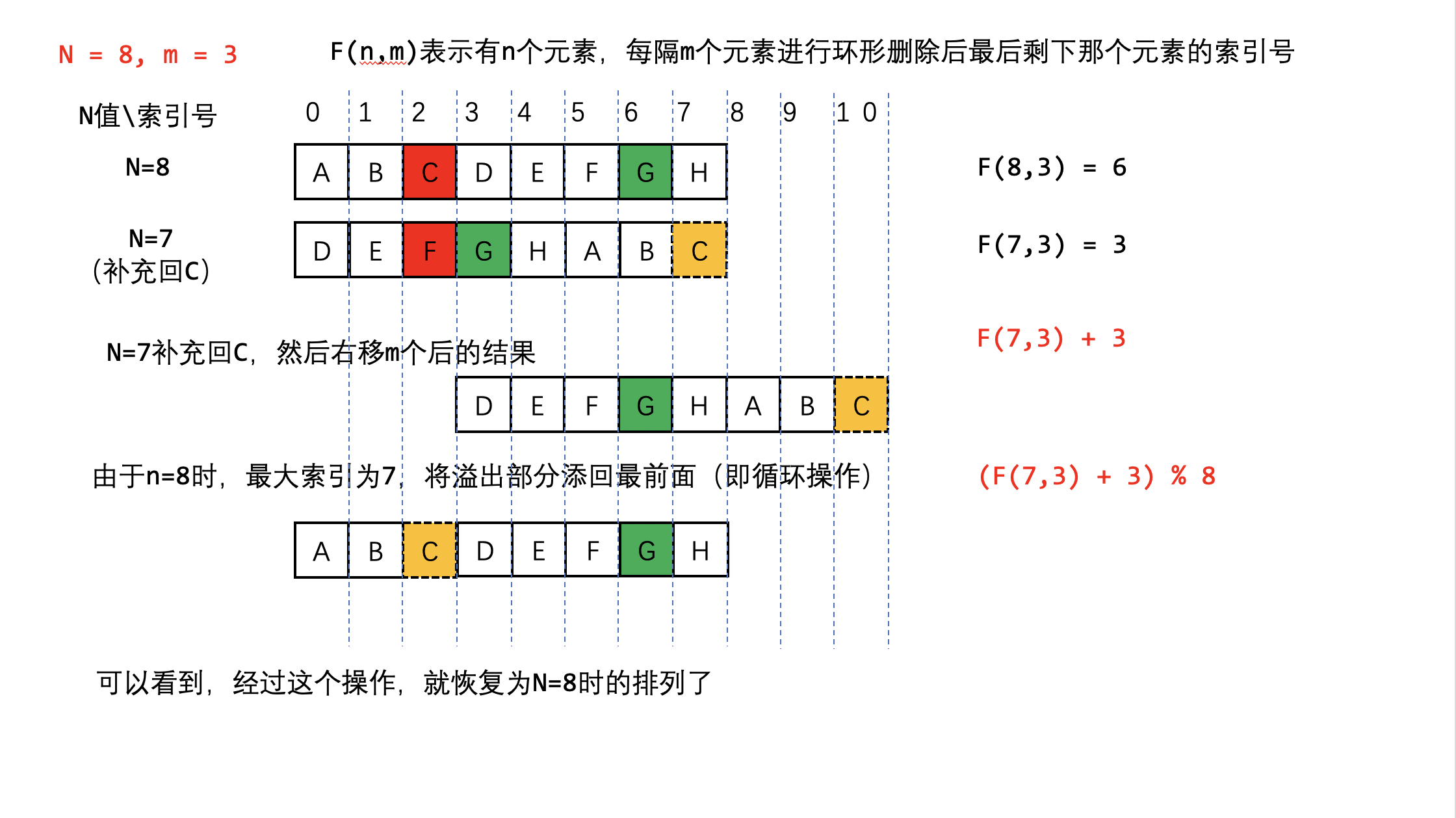
由上图可得递推公式为f(n, m) = (f(n - 1, m) + m) % n。根据此递推公式可以得出动态规划和递归解法。

解答2：动态规划

class Solution {
public:
    int lastRemaining(int n, int m) {
        int res = 0;
        for (int i = 2; i <= n; i++) res = (res + m) % i;
        return res;
    }
};