【剑指Offer-60】n个骰子的点数

问题

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

示例

输入： 1
输出： [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

输入： 2
输出： [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

解答

class Solution {
public:
    vector<double> dicesProbability(int n) {
        vector<double> res(6, 1/6.); // 将n=1的情况作为res的初始化，注意6后面的点
        for (int i = 2; i <= n; i++) {
            vector<double> ans(5 * i + 1); // 骰子数为1时数组的长度为5*i+1
            for (int j = 0; j < res.size(); j++)
                for (int k = 0; k < 6; k++)
                    ans[k + j] += res[j] / 6;
            res = ans;
        }
        return res;
    }
};

重点思路

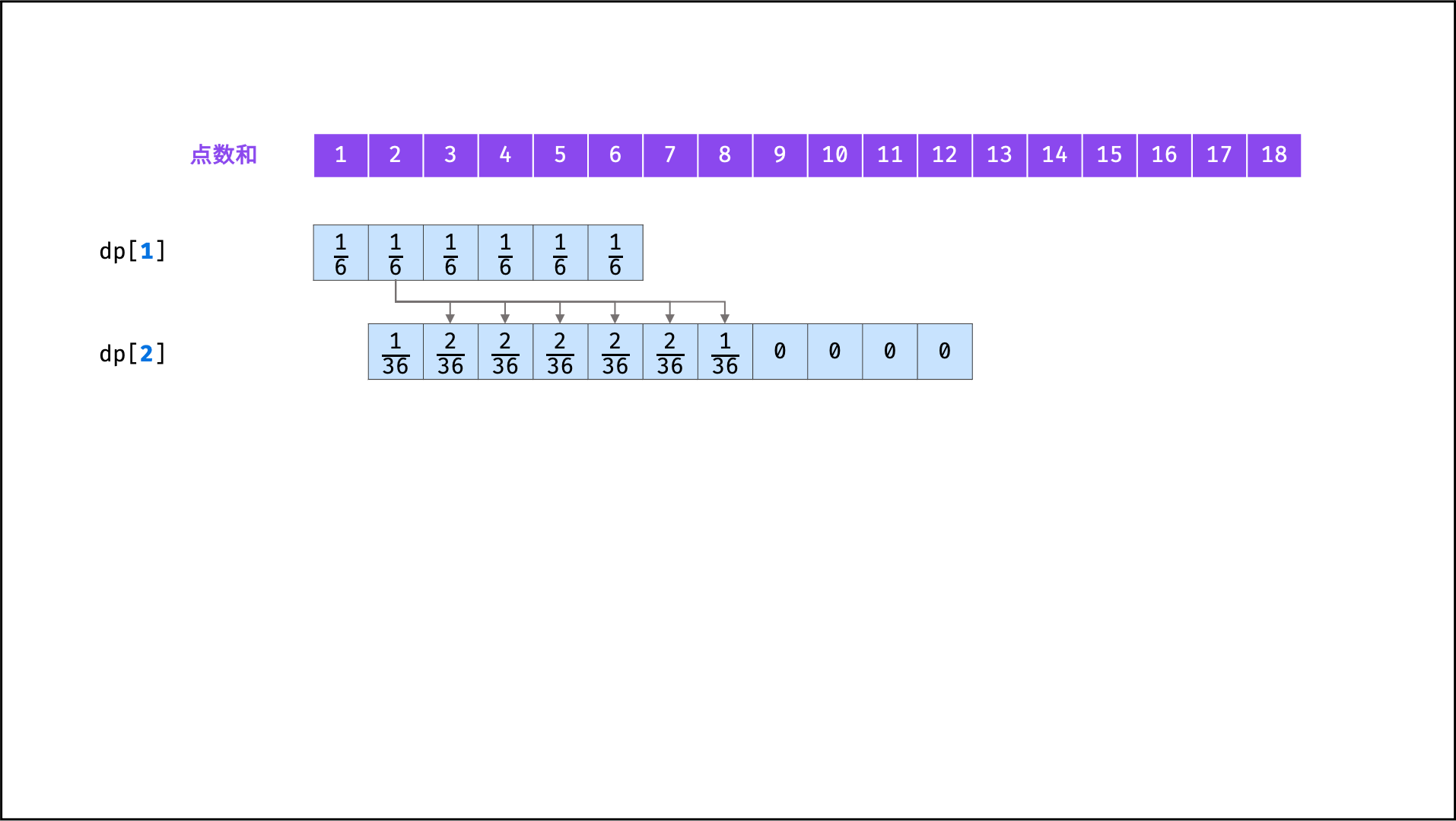
从题目要求到推导出状态转移方程这个过程非常重要。本文要求n个骰子所有情况的概率，首先考虑这个概率是否和n-1个骰子的概率有关。假设A对应n个骰子的一个状态，B对应n-1个骰子的一个状态，且A可由B转移得到（即0 < A - B < 7），则B转移到A的概率为1/6。也就是说，n-1个骰子的每个状态都有1/6的概率转移到n个骰子的可转移状态上。易得n个骰子的所有状态数量为5 * n + 1，每个状态的概率可由n-1个骰子的状态概率转移得到。