【剑指Offer-43】1～n整数中1出现的次数

问题

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

示例

输入： n = 12
输出： 5

解答

class Solution {
public:
    int countDigitOne(int n) {
        long digit = 1;
        int res = 0, high = n / 10, low = 0, cur = n % 10;
        while (high || cur) {
            if (cur < 1) res += high * digit;
            else if (cur == 1) res += high * digit + low + 1;
            else res += (high + 1) * digit;
            // ------ 变量为下一次循环做准备
            low += cur * digit;
            cur = high % 10;
            high /= 10;
            digit *= 10;
            // ------
        }
        return res;
    }
};

重点思路

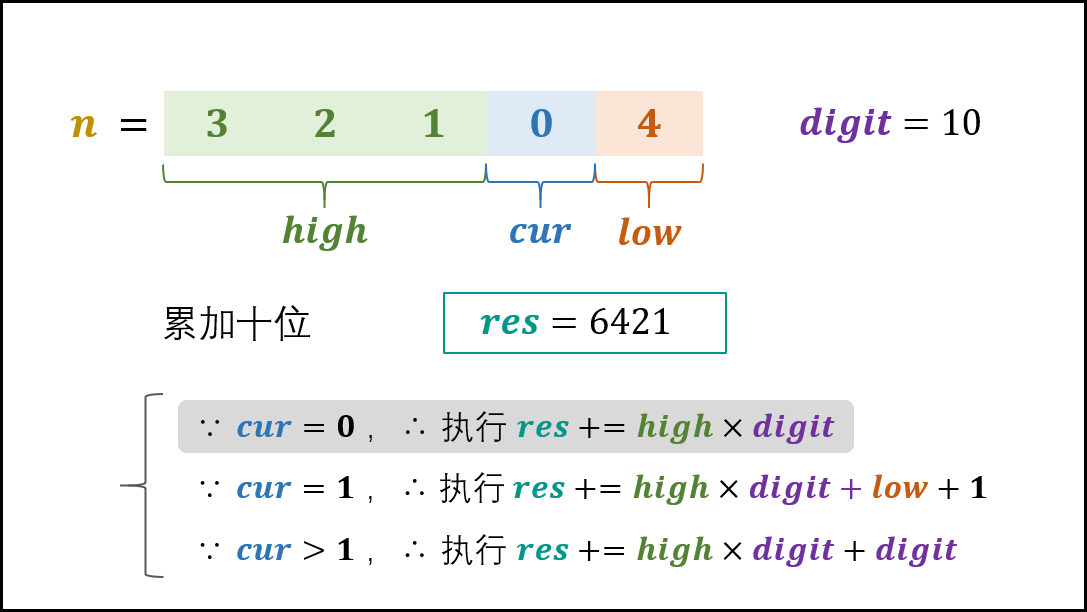
代码中的名词解释：cur为当前位，high为比当前位高的所有位，low为比当前位低的所有位，digit为当前位的“位因子”，如digit=1000时表示当前位为千位。

从低位到高位，依次统计当前位为1时，可能出现的所有情况的数量。如上图，统计十位时，当前位cur可能存在三种情况：

• 当前位的值小于统计的值（本题为1）时，当前位为1时所有情况的数量为high * digit；
• 当前位的值等于统计的值（本题为1）时，当前位为1时所有情况的数量为high * digit + (low + 1)；
• 当前位的值小于统计的值（本题为1）时，当前位为1时所有情况的数量为(high + 1) * digit；

为什么数量为这么多自己举个例子就清楚了，这里不多赘述。

拓展：求任意数字出现的次数

class Solution {
public:
    int digitCounts(int k, int n) {
        long digit = 1;
        int res = 0, high = n / 10, low = 0, cur = n % 10;
        while (high || (cur && k)) { // 变动
            if (cur < k) res += high * digit; // 变动
            else if (cur == k) res += (high - (k == 0)) * digit + low + 1; // 变动
            else res += (high + (k != 0)) * digit; // 变动
            low += cur * digit;
            cur = high % 10;
            high /= 10;
            digit *= 10;
        }
        return res + (k == 0); // 变动
    }
};

重点思路

框架是完全一样的，主要问题在于如何解决要求0出现次数的问题。下面讨论当要求的值为0时，本题会出现的特殊情况：

• 循环条件中，去掉最高位为0的情况；
• cur == k这一情况下，因为当前值为0，所以高位可利用的值会减去1；
• cur > k这一情况下，不像1有10、100、1000，0没有00、000、0000，所以高位不用加1。因为存在0，所以最后的输出要加1。