【C++】排序算法

快速排序

快速排序算法是一种非线形时间比较类排序算法，它采用了分治的思想：

1. 从数列中取出一个数（随机选择一个数。如果只取第一个数，若整个数组本身就是有序的，那时间复杂度会退化到\(O(n^2)\)）作为pivot。
2. 将数组进行划分（partition），将比基准数大的元素都移至枢轴右边，将小于等于基准数的元素都移至枢轴左边。
3. 再对左右的子区间重复第二步的划分操作，直至每个子区间不超过一个元素。

快排最重要的一步就是划分了。划分过程可以采用swap函数交换。

需要注意的是，一定要先移动右指针，再移动左指针。swap方法中，如果移动的是左指针导致的左右指针重叠，则两个指针当前指向的数是原来右指针指向的数，该值大于pivot，不能将这个值交换到当前区间的最左节点。

代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        srand(time(NULL)); // 初始化随机数种子
        quickSort(nums, 0, nums.size() - 1);
        return nums;
    }
private:
    void quickSort(vector<int>& nums, int start, int end) {
        if (start >= end) return;
        int mid = partition(nums, start, end);
        quickSort(nums, start, mid - 1);
        quickSort(nums, mid + 1, end);
    }
    int partition(vector<int>& nums, int left, int right) {
        swap(nums[left], nums[rand() % (right - left + 1) + left]); // 随机选择pivot
        int start = left, pivot = nums[left];
        while (left < right) {
            while (left < right && nums[right] >= pivot) right--;
            while (left < right && nums[left] <= pivot) left++;
            swap(nums[left], nums[right]);
        }
        swap(nums[start], nums[left]); // 这里high一定会等于low
        return left;
    }
};

归并排序

归并排序利用了分治的思想来对序列进行排序。对一个长为n的待排序的序列，我们将其分解成两个长度为n/2的子序列。每次先递归调用函数使两个子序列有序，然后我们再线性合并两个有序的子序列使整个序列有序。对于两个子序列A, B，我们需要使用一个临时数组sorted对这两个序列排序，具体方法如下：

分治示意图

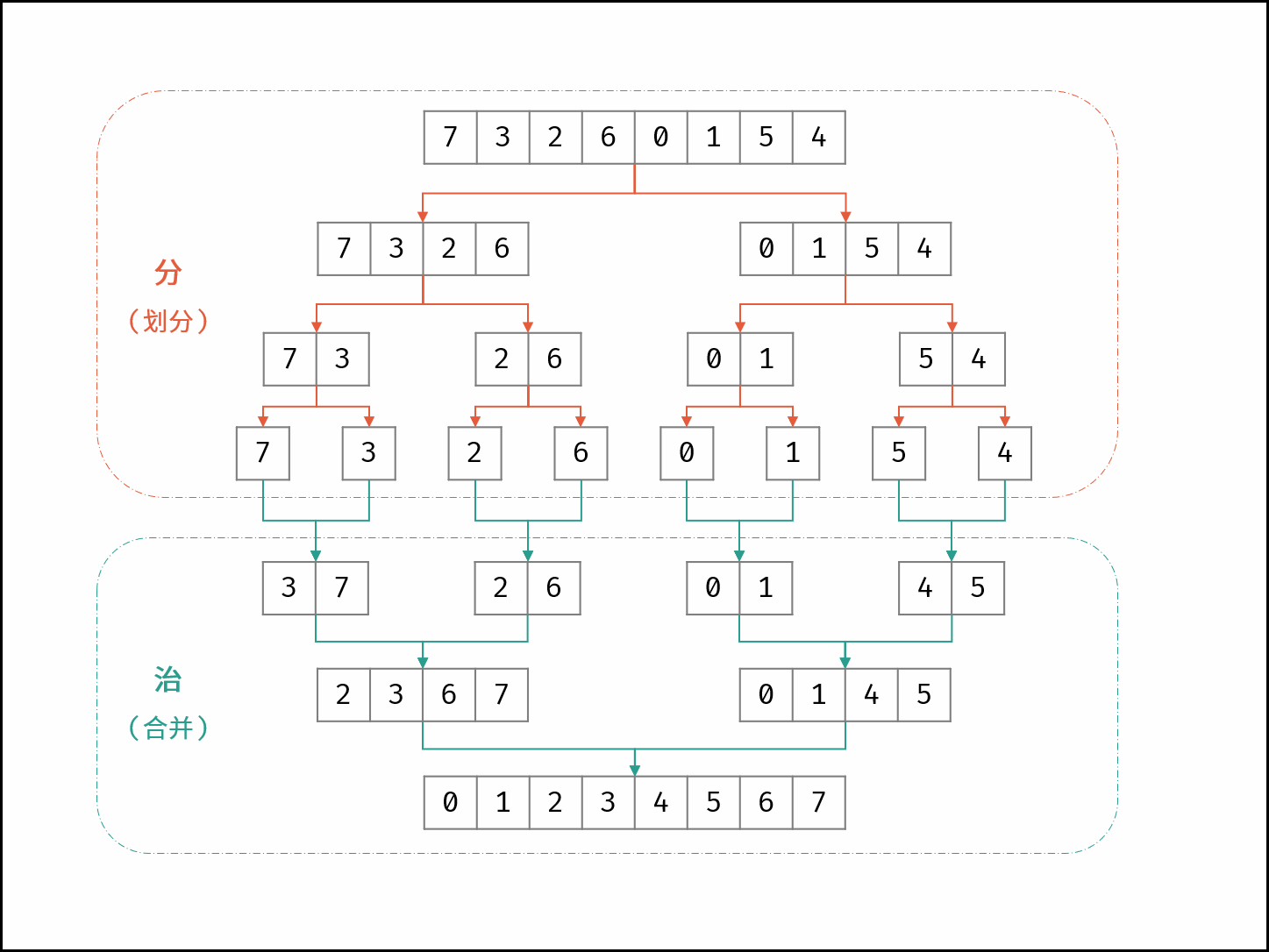
归并示意图

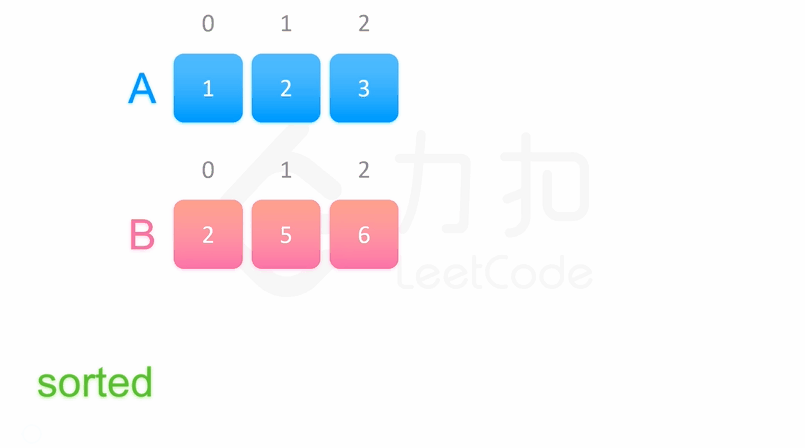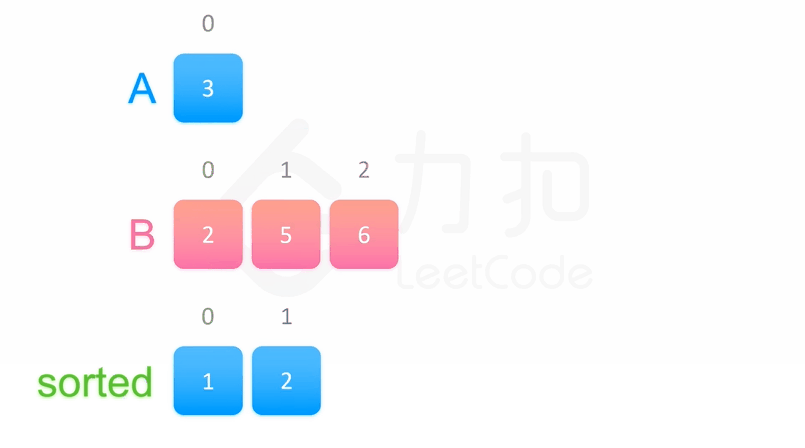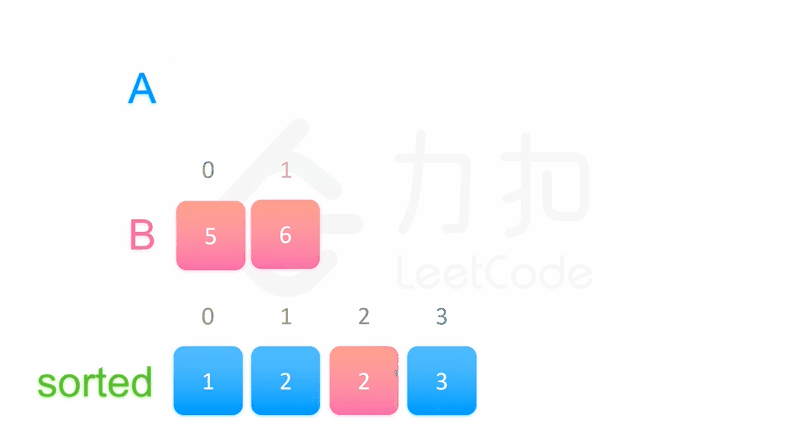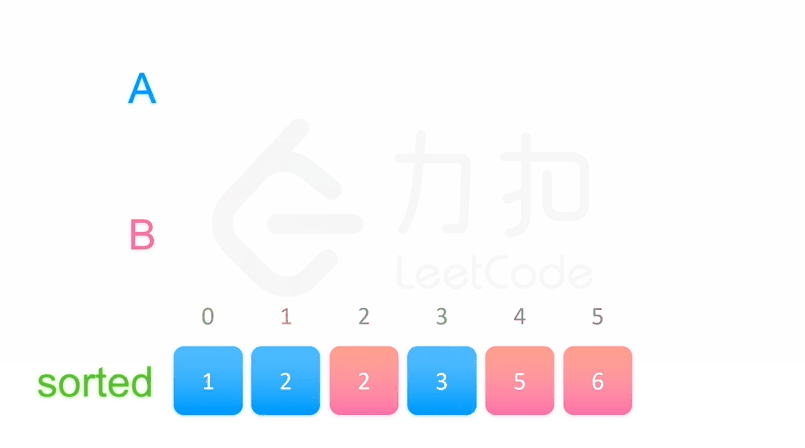
代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        tmp.resize(nums.size());
        mergeSort(nums, 0, nums.size() - 1);
        return nums;
    }
private:
    vector<int> tmp;
    void mergeSort(vector<int>& nums, int left, int right) {
        if (left >= right) return;
        int mid = left + (right - left) / 2;
        mergeSort(nums, left, mid); // 分
        mergeSort(nums, mid + 1, right); // 分
        merge(nums, left, mid, right); // 治
    }
    void merge(vector<int>&nums, int left, int mid, int right) {
        int i = left, j = mid + 1, cnt = left;
        while (i <= mid && j <= right)
            tmp[cnt++] = nums[i] > nums[j] ? nums[j++] : nums[i++];
        while (i <= mid) tmp[cnt++] = nums[i++];
        while (j <= right) tmp[cnt++] = nums[j++];
        for (int i = left; i <= right; i++)
            nums[i] = tmp[i]; // 注意tmp数组是从left开始计数的，同nums
    }
};

堆排序

堆排序使用数组模拟堆，当数组以0为起始点时，数组中nums[i]的左子节点为nums[2 * i + 1]。正序序列的堆排序先将原二叉树处理为一个大根堆，（大根堆的定义为：1. 完全二叉树； 2. 每个节点为其子树的最大值），然后取其堆顶，与其最后一个节点交换，再将其余数据重新维护为大根堆。

堆排序分两步：1. 建树； 2. 排序。

代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        for (int i = n / 2 - 1; i >= 0; i--) // 建树
            heapify(nums, i, n);
        for (int i = n - 1; i >= 0; i--) { // 排序
            swap(nums[0], nums[i]);
            heapify(nums, 0, i);
        }
        return nums;
    }
private:
    void heapify(vector<int>& nums, int i, int n) {
        int left = 2 * i + 1;
        int right = left + 1;
        int maxIndex = i;
        if (left < n && nums[maxIndex] < nums[left]) maxIndex = left;
        if (right < n && nums[maxIndex] < nums[right]) maxIndex = right;
        if (maxIndex != i) {
            swap(nums[i], nums[maxIndex]);
            heapify(nums, maxIndex, n);
        }
    }
};