【剑指Offer-28】对称的二叉树

问题

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。具体定义如下：

解答1：递归

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        return recur(root->left, root->right);
    }
private:
    bool recur(TreeNode* L, TreeNode* R) {
        if (!L && !R) return true;
        if (!L || !R || L->val != R->val) return false;
        return recur(L->left, R->right) && recur(L->right, R->left); 
    }
};

重点思路

递归三部曲：

1. 输入值与返回值：本题要比较两个子树是否对称，需要传入的参数为两个子树的根节点。返回值为true或false；
2. 终止条件：两个节点按是否为空可以划分为3种情况。当两个节点都为空时，表示这一部分子树已比较完成，均相同，返回true。当节点只有一个为空时，返回false。都不为空时，当节点值不相同时，返回false，相同时，继续递归；
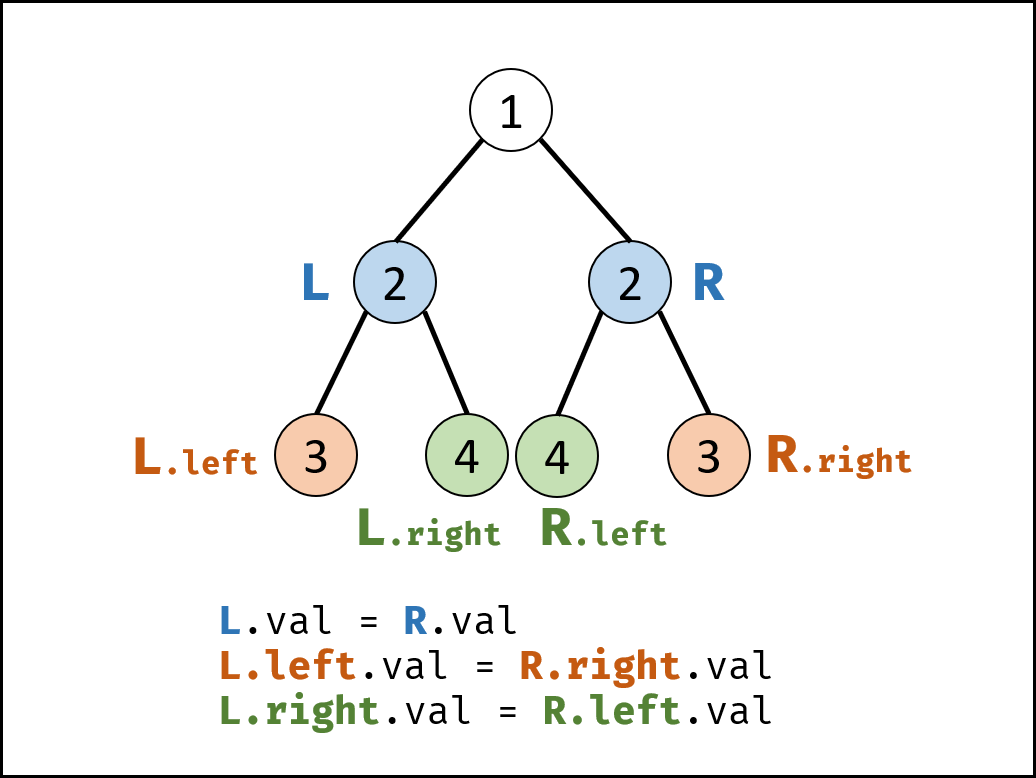
3. 单层逻辑：即第2点中没有返回值的那张情况。此时考虑一个最简单的含有3个节点的两个二叉树，我们需要比较树A的左节点是否与树B的右节点相同，以及树B的左节点是否与树A的右节点相同。

解答2：迭代

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        queue<TreeNode*> q;
        q.push(root->left);
        q.push(root->right);
        while (!q.empty()) {
            TreeNode* A = q.front(); q.pop();
            TreeNode* B = q.front(); q.pop();
            if (!A && !B) continue;
            else if (!A || !B || A->val != B->val) return false;
            q.push(A->left);
            q.push(B->right); // 组1
            q.push(A->right);
            q.push(B->left); // 组2
        }
        return true;
    }
};

重点思路

迭代方法将左右节点每两个为一组存放在队列、栈这样的数据结构中。单层的比较思路与递归方法是相同的。