【剑指Offer-26】树的子结构

问题

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构，即A中有出现和B相同的结构和节点值。

例如:
给定的树A与树B:

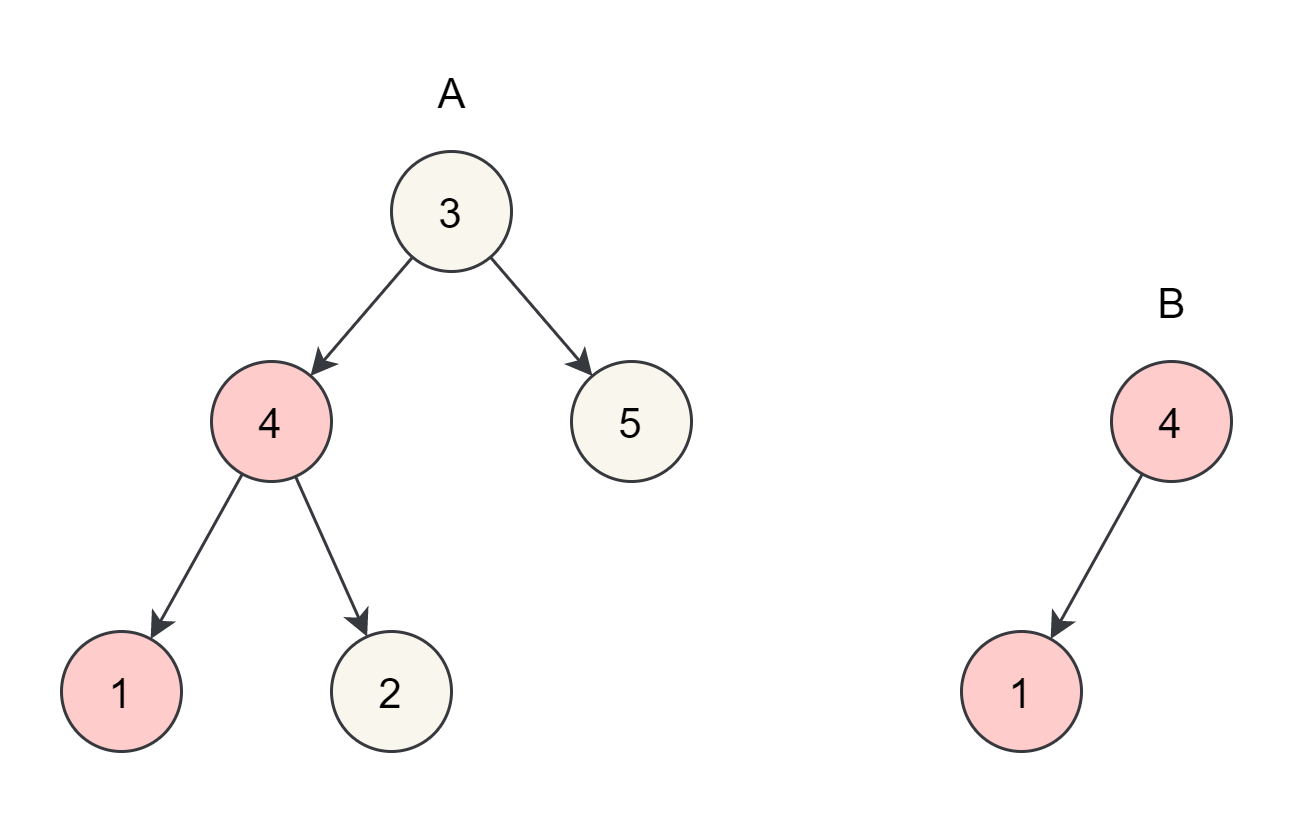
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例

输入： A = [1,2,3], B = [3,1]
输出： false

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

解答

class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if (!A || !B) return 0;
        return recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
private:
    bool recur(TreeNode* A, TreeNode* B) {
        if (!B) return 1;
        if (!A || A->val != B->val) return 0;
        return recur(A->left, B->left) && recur(A->right, B->right);
    }
};

重点思路

这道题虽然有两个递归，看起来很复杂，但是这两个递归都是用于遍历的，非常容易理解。具体遍历过程如下图所示。这里着重讨论一下几个重要语句的作用。

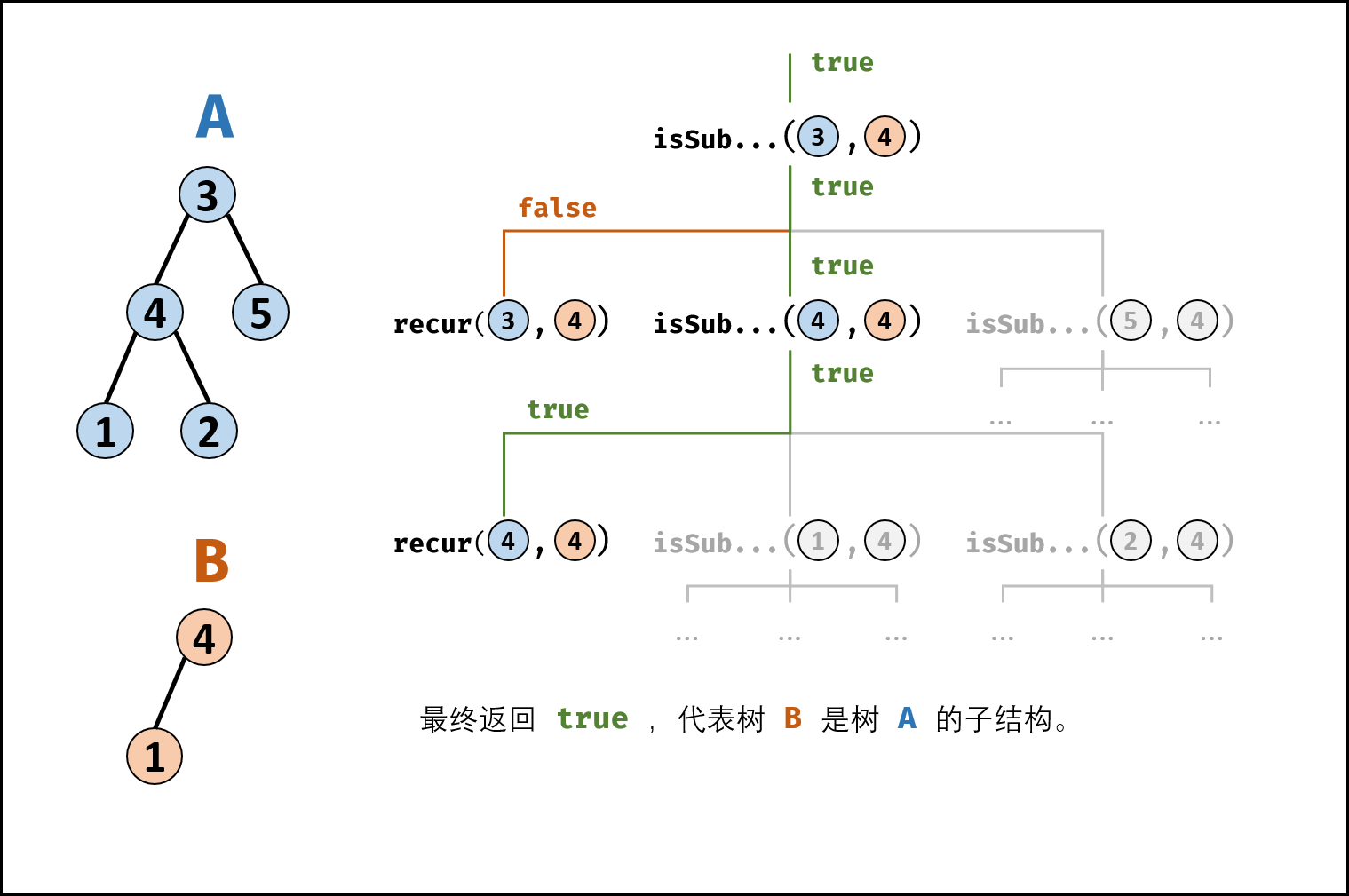
recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B))这一句首先使用recur函数判断根节点为B的树是否是根节点为A的树的子树。具体判断方法为：

• 当B节点为空时，表示B已检查完毕，符合子树要求，返回true；
• 当A节点为空时，表示B没有包含在A中，返回false；
• 当A与B节点值不相同时，返回false；
• 当B的左右子树都满足要求时，recur函数返回true。

当recur(A, B)返回true时，由于||具有截断性，所以上一条语句直接返回true；如果recur返回false，即匹配失败时，则继续对A做前序遍历，即isSubStructure(A->left, B) || isSubStructure(A->right, B)，A前序遍历的终止条件为!A。