【剑指Offer-24】反转链表

问题

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

Definition for singly-linked list.
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

示例

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

解答1：迭代（双指针）

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *cur = head, *pre = nullptr;
        while (cur) {
            ListNode *tmp = cur->next; // 暂存下一节点
            cur->next = pre; // 当前节点反转
            pre = cur; // 上一节点移动到当前节点
            cur = tmp; // 当前节点移动到下一节点
        }
        return pre;
    }
};

重点思路

遇到链表操作问题一定要先画图整理思路。搞清楚每一次迭代前后链表的状态，从而确认每一次迭代的具体操作，以及迭代的终止条件，整理好这些思路后再写代码。

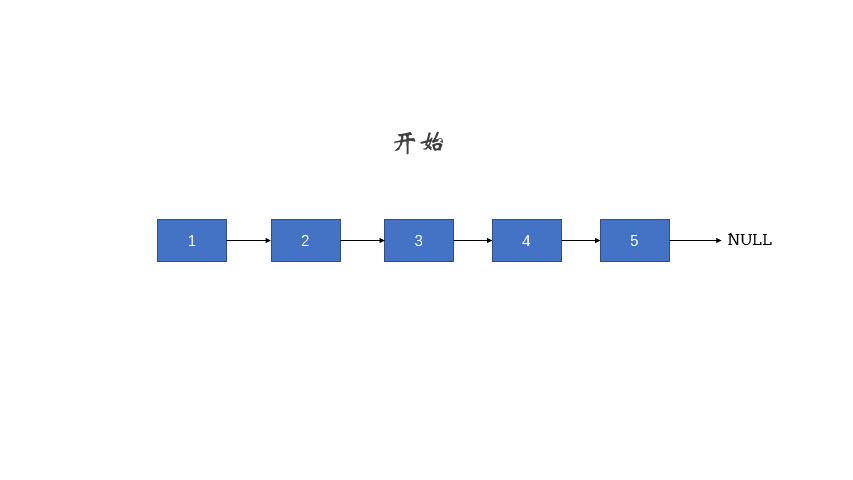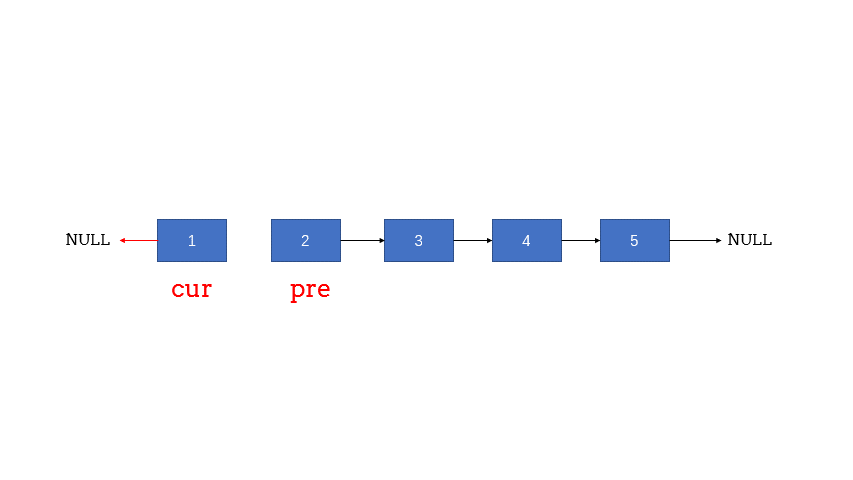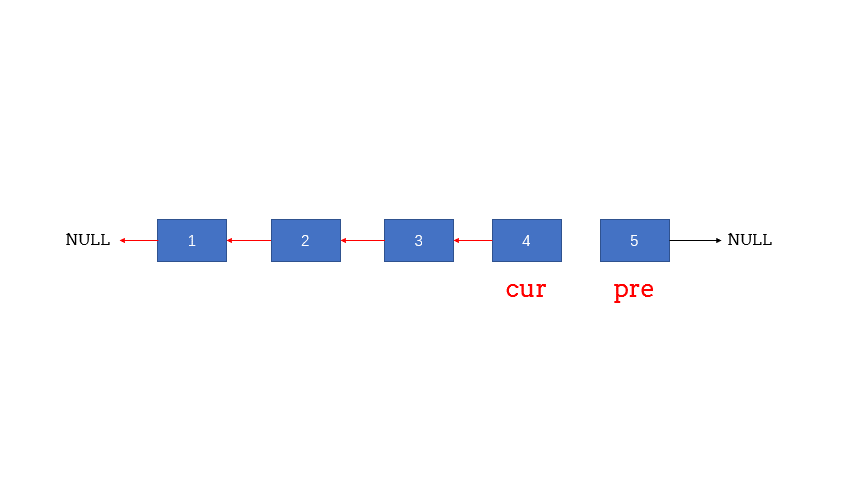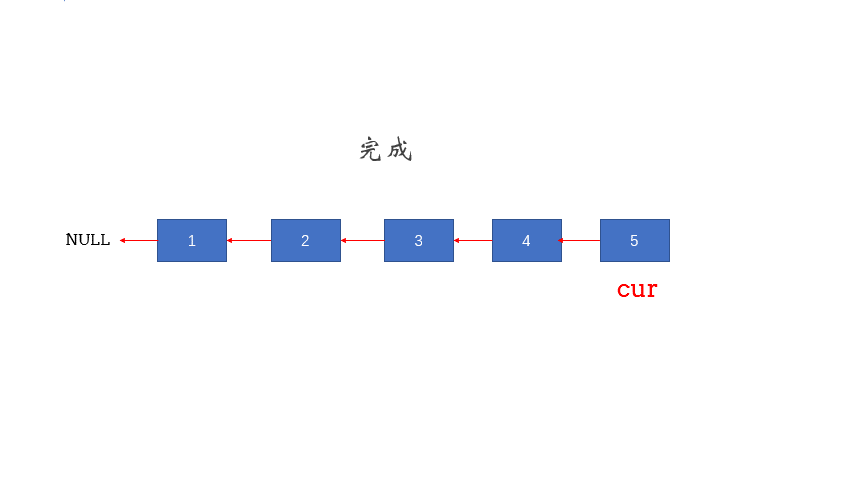
解答2：递归

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) return head; // 前者防止输入空链表，后者为递归终止条件
        ListNode *res = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return res;
    }
};

重点思路

首先说一个递归的禁忌，就是尝试想用大脑去模拟递归实际计算时的层层调用层层返回这一过程。递归问题的求解方法可以总结为：1.找能求解“大问题”的“小问题”；2.根据这个“小问题”找递归的终止条件；3.弄明白我们最后要的是什么； 4.找通过“小问题”求解“大问题”的具体方法（递推条件）。感觉和解决动态规划题的思路的区别就是一个是自底向上，一个是自顶向下。

对于本题，举一个简单的例子，我们反转链表1->2->3->NULL，针对上面的思路，我们可以拆分为：

1. 该问题对应的“小问题”为反转链表2->3->NULL；
2. 递归终止条件也很容易想到，就是当“小问题”为空链表时，就终止调用开始返回；
3. 我们最后要返回反转后的链表，而头节点是不变的，那么就需要把头节点一层一层返回回去；
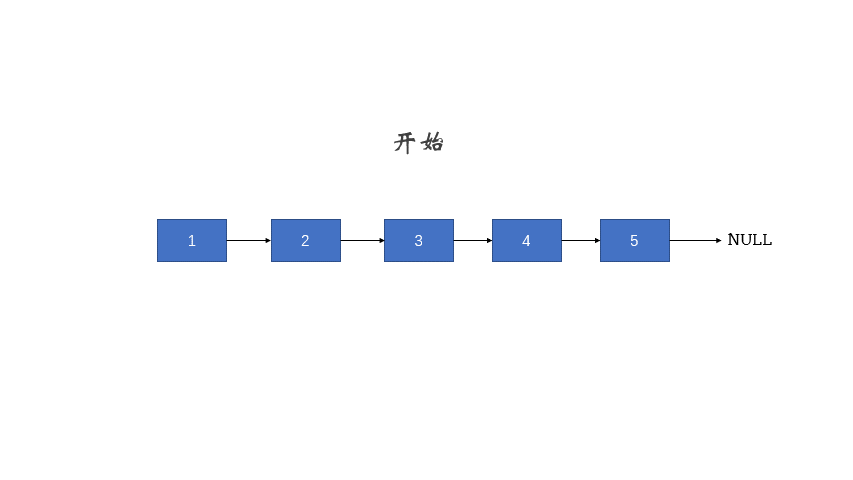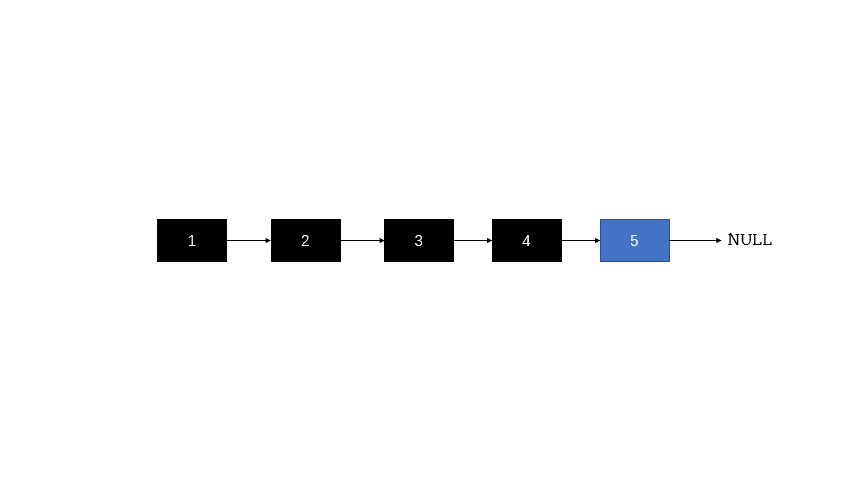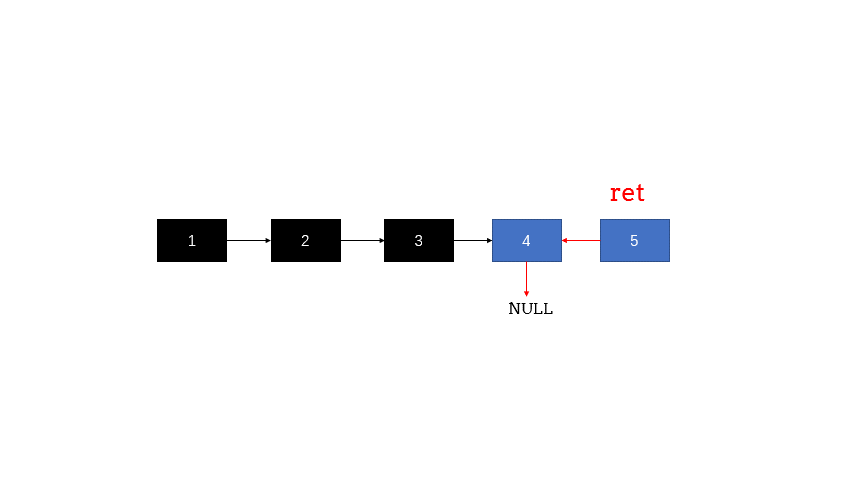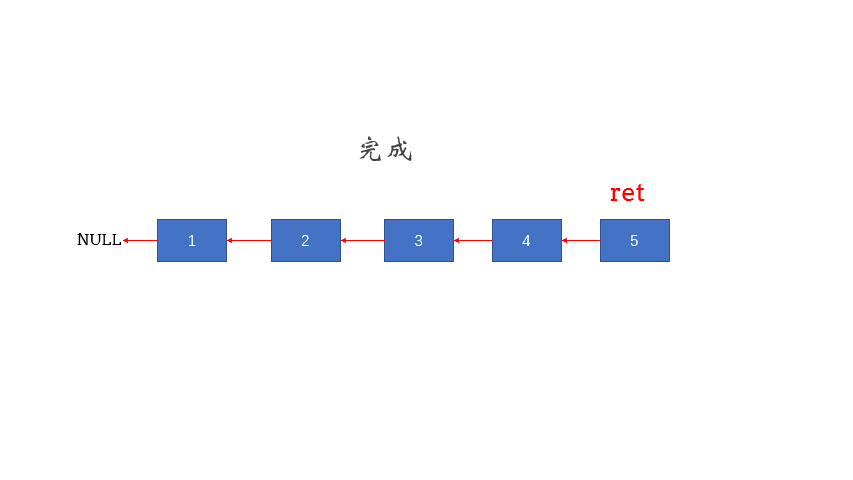
4. 最后一步就是递归问题的重难点：如何确定“小问题”到“大问题”的递推条件。换一个说法，如何从NULL<-2-<3变成NULL<-1<-2<-3。此时，head指向1，head->next指向2，那么我们需要的操作就是将head->next的下一个节点指向head，而head的下一个节点指向NULL即可。

下图为了方便了解整体流程，但在做题的时候切忌去考虑整体流程的具体调用和返回，只需要考虑子问题即可。