分类任务评价指标

Confusion Matrix

横轴为预测值，纵轴为真实值。在二分类问题上，就是分别代表TP、FP、TN、FN这四个含义。同样可以引申到多分类问题上。

from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
cm = confusion_matrix(y_true, y_pred_class)
tn, fp, fn, tp = cm.ravel() # 只适用于二分类，cm为一个二维数组

比起标准化后的数据，混淆矩阵能够更清楚地反应模型在各类型上，特别是在非平衡样本上的表现：预测对的占多少比例、预测错的是如何错的。

FPR（ROC曲线的横轴）

真实值为假的样本中，模型预测为真的概率。优化这个目标是为了保证尽可能不抓错人，即使付出漏抓的代价。因为分母为样本真实值为假的数量，所以这个指标有一定的对抗样本不平衡的能力。但是其取值收到阈值的影响，可以不随模型的意志而变化。阈值变高，只有概率更高的样本会被预测为正样本，FP会下降，分母不变，故FPR降低。

\[FPR=\frac{FP}{FP+TN} \]

from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
false_positive_rate = fp / (fp + tn)

TPR(Recall)

召回率，又成为查全率，即真实值为真的样本中，模型预测为真的概率。优化这个目标是为了保证尽可能不漏抓人，即使付出抓错人的代价。可以看出这个目标是和FPR完全相反，但都收到阈值的影响，后续会讲到平衡这两个指标的方法。将recall与FPR结合就是ROC曲线，将recall与precision结合就是F-score。

\[Recall=\frac{TP}{TP+FN} \]

from sklearn.metrics import recall_score

y_pred_class = y_pred_pos > threshold
recall_score(y_true, y_pred_class)

Precision

精确度，又成为查准率，即预测为真的样本中，实际上是真的概率。优化这个目标是为了保证抓的人要尽可能抓对。以上三种指标单独使用都没什么意义，需要联合评价来衡量模型性能。

\[Precision=\frac{TP}{TP+FP} \]

from sklearn.metrics import precision_score

y_pred_class = y_pred_pos > threshold
precision_score(y_true, y_pred_class)

Accuracy

在所有样本中，预测正确的概率。该指标受到类别不平衡影响非常严重，设样本label为1的占总数的99%，如果仅以此为优化目标，则模型容易变成一个全肯定bot。

\[ACC=\frac{TP+TN}{TP+FP+FN+TN} \]

from sklearn.metrics import accuracy_score

y_pred_class = y_pred_pos > threshold
accuracy_score(y_true, y_pred_class)

F-score

即recall与precision的加权调和平均数。调和平均数会更重视变量中的偏小值，当变量存在相互制约关系时，如\(x+y=1\)或\(xy=1\)，调和平均数越高，模型能取得更好的变量间trade-off。即该值越高，模型性能越好。如果更关心召回率，则设置更高的\(\beta\)。当\(\beta^2=1\)时，F-score为F1-score，当\(\beta^2=2\)时，为F2-score，此时可看作recall重要性为precision两倍。

\[F_{beta}=\frac{\beta^2+1}{\frac{\beta^2}{recall}+\frac{1}{precision}} \]

from sklearn.metrics import fbeta_score

y_pred_class = y_pred_pos > threshold
fbeta_score(y_true, y_pred_class, beta)

recall和precision都是高度依赖于阈值的，故调整阈值有利于F-score的提升。使用kfold，在oof上可以调整阈值，前提条件是线上线下要一致，也就是说每个kfold的训练集分布尽可能要和测试集分布相同。

Kappa

Kappa在多分类任务和非平衡数据上表现较好。该指标反应该模型比随机分类器的性能好多少，取值范围-1到1，越高越好。

Kappa能够衡量真实数据与预测数据之间的一致性。计算公式为如下。

\[\kappa=\frac{p_{o}-p_{e}}{1-p_{e}} \]

其中，\(p_{o}\)(observed agreement)为accuracy，\(p_{e}\)(expected agreement)的定义为：假设每一类的真实样本个数分别为为\(a_{1}, a_{2}, \ldots, a_{c}\)，而预测出来的每一类的样本个数分别为\(b_{1}, b_{2}, \ldots, b_{c}\)，总样本个数为\(n\)，则：

\[p_{e}=\frac{\prod_{i=1}^{c}a_ib_i}{n^2} \]

举例：

学生考试的作文成绩，由两个老师给出 好、中、差三档的打分，现在已知两位老师的打分结果，需要计算两位老师打分之间的相关性kappa系数：

\[\begin{cases} p_{o}=\frac{(10+35+15)}{87} = 0.689\\ a_1=10+2+8=20\\ b_1 = 10+5+5 = 20\\ \ldots\\ p_e=\frac{a_1b_1+a_2b_2+a_3b_3}{8787}=0.455 \end{cases} \]

\[\kappa=\frac{p_{o}-p_{e}}{1-p_{e}}=0.4293578 \]

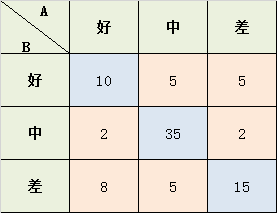
from sklearn.metrics import cohen_kappa_score

cohen_kappa_score(y_true, y_pred_class)

kappa为带阈值指标，同样可以调整阈值取得更好的kappa。

ROC AUC

ROC曲线

直观地显示了TPR(recall)和FPR之间的权衡。对于每个阈值计算TPR和FPR，并将其绘制在一条曲线。该曲线即为ROC曲线。

对于每个阈值，TPR越高、FPR越低越好，因此曲线越靠近左上角，模型性能越好。

from scikitplot.metrics import plot_roc

fig, ax = plt.subplots()
plot_roc(y_true, y_pred, ax=ax)

AUC(Area Under the ROC Curve)

模型评价(一) AUC大法_weixin_34148340的博客-CSDN博客

我们对AUC有两个不同但等价的定义：

• AUC为ROC曲线下方围成的面积大小。
• AUC反映分类器对样本的排序能力：AUC反映的是正样本的预测结果大于负样本预测结果的概率。

故AUC的计算公式可以从两个方面来考虑：

• 使用提供样本点，使用模型估计得到对每个样本的评分后绘图。最后，计算途中相邻样本间围成的梯形面积，相加得到AUC估计值，样本越多越准确。
• 使用提供样本点，使用模型估计得到对每个样本的评分。使用样本中正样本的预测结果大于负样本预测结果的频率估计概率，样本越多越准确。

第一种做法计算过于繁琐，故考虑第二种做法。

第二种做法分为两个方法。设正样本数为M，负样本数为N。

1. 将样本分为\(M\times N\)个二元组，每个二元组包含一个正样本和一个负样本，判断模型对这两个样本预估得到的评分是否满足正样本大于副样本。AUC等于满足上述条件的二元组个数除以所有二元组个数，时间复杂度为\(O(MN)\)。
2. 将模型对所有样本估计得到的评分排序，根据排序结果为每个样本设定rank值，rank范围为\([1,M+N]\)。将正样本的rank值进行加和，得到的是正样本大于负样本的总数，但这个总数也将二元组中两个都是不同或相同的正样本这种情况统计在内，故需要减去\(C_{M+1}^2\)，时间复杂度为\(O(M+N)\)，最终的公式如下：

\[AUC=\frac{\sum_{i\in positiveClass}rank_i-C_{M+1}^2}{M\times N} \]

from sklearn.metrics import roc_auc_score

roc_auc = roc_auc_score(y_true, y_pred_pos)

PR曲线

对每一个阈值计算其precision和recall，画出曲线图，即PR曲线。

from scikitplot.metrics import plot_precision_recall

fig, ax = plt.subplots()
plot_precision_recall(y_true, y_pred, ax=ax)

Log loss

log损失通常被用作机器学习模型下的优化目标函数，但它也可以作为性能度量。但通常不这么用。

\[log\_loss=-(y \log (p)+(1-y) \log (1-p)) \]

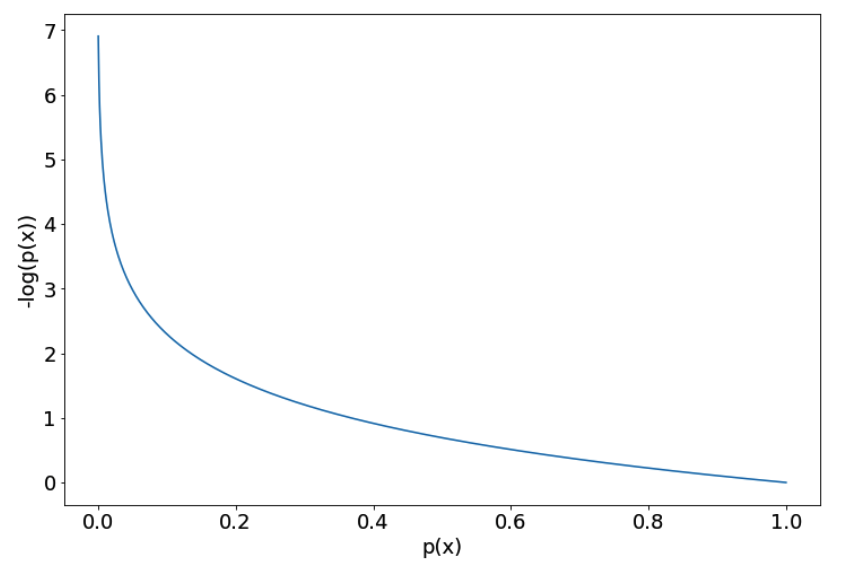
上图为label=1时的损失函数，可以看出，当预测值为0时模型收到严重惩罚。这通常也会导致一些问题，所以加上梯度裁剪是一个合理的选择。

from sklearn.metrics import log_loss

log_loss(y_true, y_pred)