机器学习基石4-在何时才能使用机器学习（4）

            向杜少致敬! 

Lecture 4: Feasibility of Learning

 

4.1. Learning is Impossible?

　 

                                                                    图 4-1

 Q1：在训练集 （in-sample） 能找到一个 g ≈ f, 但是你不能保证在应用数据 （out-sample）还有 g ≈ f 。

 Q2：就算在某种约束下，你能保证在应用数据 （out-sample） g ≈ f。 如果我有多个 g ≈ f， 即 g₁ ≈ f、g₂ ≈ f、g₃≈ f、… g_n ≈ f。 如何找到在 out-sample 上性能最好的 g_opt 呢？

 

4.2. Probalility to the Rescue

    learning 是做不到的！但是我们可以想一下，有没有学习用少量的已知的事实去推测整个样本的情况？ 现在给你一个罐子，你能给出黄绿弹珠所占的比例是多少？ 假设黄绿弹珠的分布较均匀，可以通过抽样的方法获取黄绿弹珠的比例。

                         图 4-2

       假设在抽出的样本中 orange marble 的比例是 v， green marble 的比例是 1 -v。 罐子中的 orange marble 的比例是 μ， green marble 的比例是 1-μ。

v 和 μ 基本不相同，那要在什么样的条件下？ v 和 μ 才能足够的接近？在数学中有个 Hoeffding's Inequality 能刻画出 v 和 μ 的接近程度。

                                $$ \mathbb{P} [|\nu -\mu |] \leqslant 2 exp(-2\epsilon^2N)  $$

                                                                       公式 4-1

      Hoeffding 不等式的良好性质：

　　     1. 只和 N、ε有关，和 μ、ν 无关

            2. N 越大或 ε 越大， v 和 μ 大概近似正确（probably approximately correct PAC）

 

Q3：HOeffding 不等式和切比雪夫不等式的关系？

Q4：回忆一下以前学过的中心极限定理、大数定理

 

4.3. Connection to Learning

       上一节，我们一直在玩弹珠游戏。这个和机器学习有什么关系呢？

假设我们有一罐白色弹珠，  这些弹珠有某些性质。我们准备用机器学习去预测这些弹珠的性质。 假设我们有个 g， 如果 g(x) = f(x) 则将弹珠染绿并放到罐子 B 中， 如果 g(x) != f(x) 则将弹珠染黄并放到 B 中。最终我们会得到罐子 B 会如下图所示。

            图 4-3

       现在有一罐装满黄绿弹珠的罐子， orange marble 代表我们预测这个 marble 时出错了， green marble 代表我们成功地预测这个 marble。 这样就回到上一节。

现在，我们可以保证在 in-sample 上 g 和 f 的 pac 近似。 但是我们不能保证 g 和 f 的差别不大。 如果说 orange marble 的出现概率在 in-sample 和 out-sample 是 pac 近似正确，但是 orange marble 的比例很大。这也不是我们想要的， orange 出现比例越大说明 g 越不准确。而且我们是用一个固定的 g ，没有学习的过程。不能算是学习，当然也不会是机器学习

 

4.4. Connection to Real Learning

 

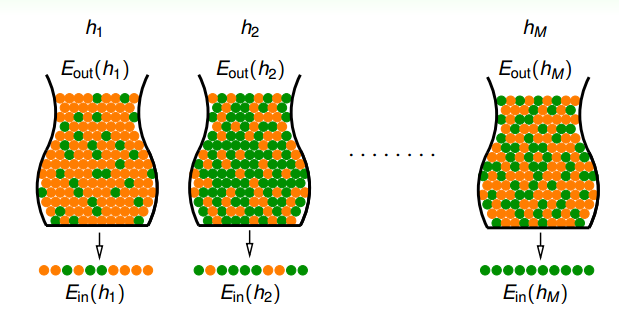
                                                                 图 4-4

      4.3 节时，我们不能保证选取那一个 h 和 f 足够的接近，我们将所有的 h 拿出来给白色罐子染色。假设我们对某个罐子 sample 出来的 marble 全是 green。是不是就可以说这个罐子对应的 h 就是我们想要的？

因为有 Hoeffding 不等式，从直觉上来说这应该是对的。

                                                                  图 4-5

     假设有150个人同时丢五次硬币，统计其中有一个人丢出五次全部正面向上的概率是多少，不难得出一个人丢出五次正面向上的概率为 1/32。在 150 人有一个人投出全是正面的概率为 1 - (31/32)¹⁵⁰ > 99%。

这说明在图 4-5 中，某个罐子中 sample 出来的 marble 全是 green。也不能说明这个罐子对应的 h 是好的。我们将这种 E_in  和 E_OUT  差别很大的 sample 起个新名字 —— BAD SAMPLE。现在我们引入一个新的 concept BAD DATA， 以及简单地看下它的性质（也就是看图不说话）

 

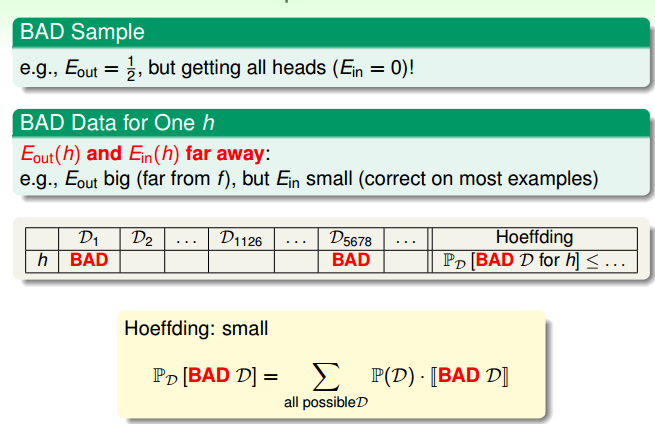
                                                                图 4-6

      将每次抽样的数据集称做 DATA， 如果在这个 DATA 上E_in  和 E_OUT  far away， 我们称之为 BAD DATA。 根据 Hoeffding 不等式，BAD DATA 出现概率非常的小。

 

                                                           图 4-7

          如果某个 DATA 在某个 h 表现不好， 就将 DATA 标记为 BAD。现在我们想知道在整个 hypothesis  空间上，踩到雷的概率上限是多少？

在 hypothesis 有 M 个h，那么可以得出踩雷的上限如公式 4-2 所示

 

          $$ \mathbb{P_\mathcal{D}} [BAD  \mathcal{D}] \leqslant 2 exp(-2\epsilon^2N) + 2 exp(-2\epsilon^2N) + ... + 2 exp(-2\epsilon^2N) = 2M exp(-2\epsilon^2N) $$         

                                                                                                   公式 4-2

       如果 M 是有限的，  E_in  = E_OUT 是 PAC， 和具体的 hypothesis 无关。在这种情况下，学习策略是选择 E_in 最小的 g。对于有无限 hypothesis 的讨论在未来的课程。

                                                

题外话：

      本文中提到了 PAC， 可以参考一下《西瓜书》上面的讨论。里面有恰 PAC 可学习、PAC 不可学习等几个概念和证明（具体忘了）。后续笔记还有 pac 理论的升级版 ---- VC 维

      4.3 节 Connection to Learning 是按照自己写的，没有严格跟着 ppt 走。

      Q1 ： 本文部分地回答了 Q1 问题，即有限假设空间下我们能 PAC 保证 g ≈ f

      Q2： Q2 问题算是机器学习中终极问题，涉及到的概念有 bias、variance、欠拟合、过拟合等。不容易回答

      Q3： 从图 4-8 可以看出，切比雪夫不等式刻画的是 期望、ε 间的关系  

                   

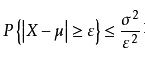
                        图 4-8

       Q4： 我所接触过的大数定律有三个，分别是切比雪夫大数定律、伯努力大数定律（见图 4-9）、辛钦大数定理 （见图 4-10）。

                      图 4-9

               图 4-10

      中心极限定理的啥，后续补上吧