解题报告： luogu P6476&NOIOR2 T1
一种新的解法，对数论能力要求更低！
考场上推错式子了，只有 25 分.....
题目链接：P6476 [NOI Online #2 提高组]涂色游戏（民间数据）
声明：此文中用 \(x,y\) 代表 \(p1,p2\) ，\((x,y)\) 指 \(\gcd(x,y)\)当然还可能是开区间，\([x,y]\) 指 \(lcm(x,y)\)当然还可能是闭区间，并满足 \(x<y\)。
我们做这个题的第一反应一定是这样的：
每隔一个 \(y\) 倍数的区间都有 \(\left\lfloor\dfrac{y}{x}\right\rfloor\) 个 \(x\) 的倍数出现，然后和 \(k\) 比大小即可。
然而被无情 hack 了，such as:
输入：
1
5 9 2
输出：
NO
我们发现在 \((9,18)\) 中有 \(2\) 个 \(x\) 的倍数：\(10\)，\(15\)。
那我们可以利用一个规律：
在 \(y\) 和 \(x\) 没有整除关系时，每一段 \(y\) 内 \(x\) 倍数出现次数 \(\in\{\left\lfloor\dfrac{y}{x}\right\rfloor,\left\lfloor\dfrac{y}{x}\right\rfloor+1\}\) 。
为什么呢？
我们设 \(z=\left\lfloor\dfrac{y}{x}\right\rfloor\)。
首先不可能更少的次数，因为 \((0,y)\) 中浪费最少了。
假如存在更多的次数，比如 \(z+2\)，
中间的空隙算上就已经 \(>y\) 了。
显然得证。
所以最上面的解法只存在一种可能：
我们设第一次在 \(y\) 区间内出现 \(z+1\) 个 \(x\) 倍数的区间为\((my,(m+1)y)\)，其中的 \(x\) 分别为 \(kx,(k+1)x......(k+z)x\)。
那么这个区间是样的：
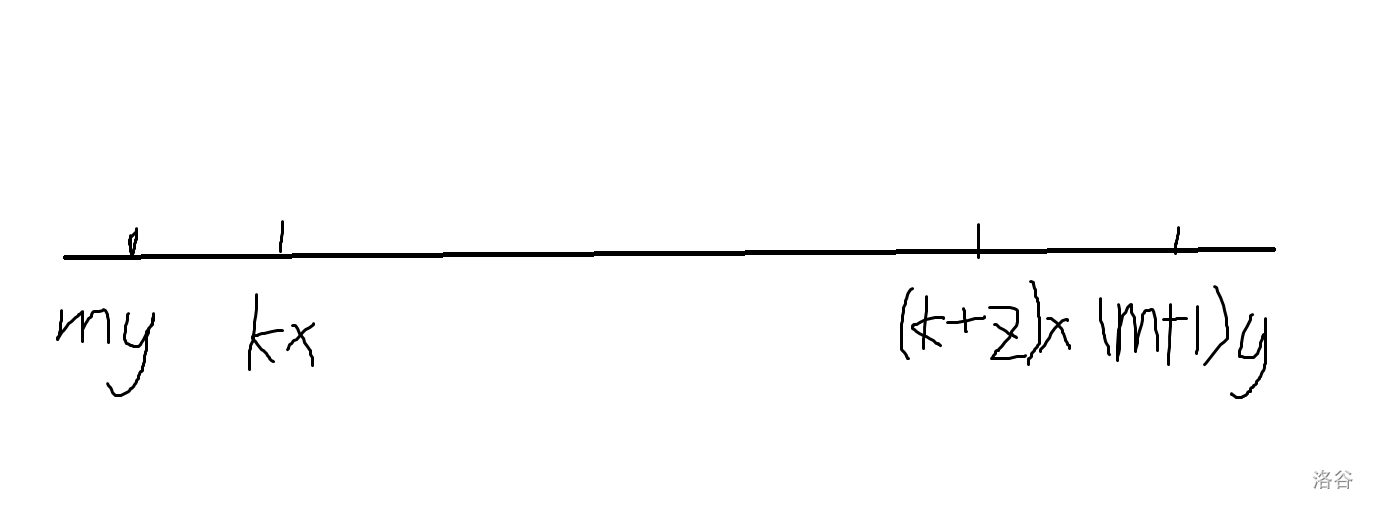
（字丑不要介意啦quq
此时显然满足：
我们注意：
我们定义的数都是第一次出现这种情况的，所以显然：
结合一下：
容易解得：
显然在 \(y-zx=0\) 即 \(x|y\) 是无意义，我们需要特判一下，循环节只有一个有 \(z-1\) 个数，这时候直接判断即可。
这就完了吗？
并没有，我们显然发现每个 \(y\) 区间的 \(x\) 倍数出现数在每个 \([x,y]\) 长的区间都有循环节。
那么显然：
容易得到：
也就是：
还有一个条件:
那么问题转化成了：
是否存在整数 \(m\) 满足：
这些过程是可以直接模拟的。
代码如下：
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define read(x) scanf("%d",&x)
int t,x,y,z,k;
double l,r;
int g;
inline int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
int check(double l,double r)//判断区间是否有正整数
{
if(l>r) return 0;
l=ceil(l),r=floor(r);
if(l<=r) return 1;
else return 0;
}
int main()
{
read(t);
while(t--)
{
read(x),read(y),read(k);
if(x>y) swap(x,y);
if(k==1){printf("NO\n");continue;}
else if(y%x==0)
{
z=y/x-1;
if(k<=z){printf("NO\n");continue;}
else{printf("YES\n");continue;}
}
else
{
z=y/x,g=gcd(x,y),g=x/g;
if(k<=z){printf("NO\n");continue;}
else if(k==z+1)
{
l=max((double)0,((double)(z+1)*(double)x-(double)y)/(y-z*x));
r=min(double(g),(double)x/(y-z*x));
if(check(l,r)){printf("NO\n");continue;}
else printf("YES\n");
continue;
}
else{printf("YES\n");continue;}
}
}
return 0;
}
然而这样只有 \(85\;pts\),为啥呢？
因为我们要判断的区间有可能是这个亚子：
我们需要一个小 trick ,运用极限思想，把区间改成这样：
就可以 \(AC\) 了。
总的来说，这种做法比小学奥数还小学奥数，只要够细致就可以得到答案。
最后附上 \(AC\) 代码：
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define read(x) scanf("%d",&x)
int t,x,y,z,k;
long double l,r;
int g;
inline int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
int check(double l,double r)
{
if(l>r) return 0;
l+=0.0000001,r-=0.0000001;
l=ceil(l),r=floor(r);
if(l<=r) return 1;
else return 0;
}
int main()
{
read(t);
while(t--)
{
read(x),read(y),read(k);
if(x>y) swap(x,y);
if(k==1){printf("NO\n");continue;}
else if(y%x==0)
{
z=y/x-1;
if(k<=z){printf("NO\n");continue;}
else{printf("YES\n");continue;}
}
else
{
z=y/x,g=gcd(x,y),g=x/g;
if(k<=z){printf("NO\n");continue;}
else if(k==z+1)
{
l=max((double)0,((double)(z+1)*(double)x-(double)y)/(y-z*x));
r=min(double(g),(double)x/(y-z*x));
if(check(l,r)){printf("NO\n");continue;}
else printf("YES\n");
continue;
}
else{printf("YES\n");continue;}
}
}
return 0;
}
