LCA之tarjan离线
显然81篇题解是有点多了,不让我提交。
更为不好的是没有一篇详细的\(tarjan\)(不过我也不会写详细的)。
不过\(tarjan\)并没有我们想象的那样难理解,时间也并不爆炸(巧妙的跳过难写二字)。
好了,下面说一说吧:
\(LCA\)是什么该都知道吧(都翻到我博客了qwq)
度娘这样认为:对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。
直观的图:

呵呵,活跃下气氛。
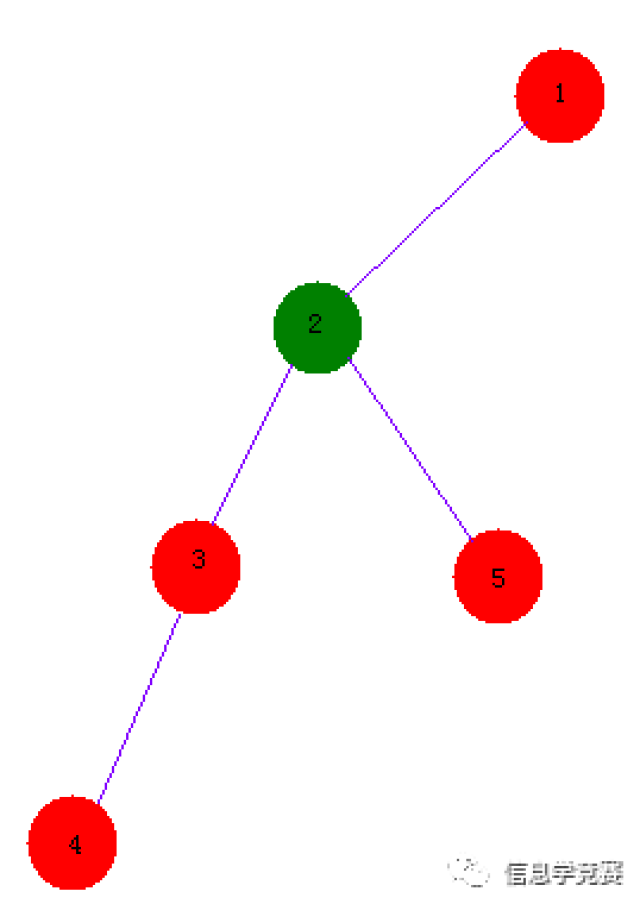
图中3,5节点的\(LCA\)为2号节点,2,4节点的\(LCA\)为1号节点。
前言:
这题数据贼水的,就算在他还是蓝题的时候(我知道数据没变),依题意暴力即可,开不开\(O2\)都是90分,\(#2\)死活不过啊,交了三四十次的样子。
如果想看代码,就点我。
\(tarjan\)求节点\(LCA\)的算法与求割点、强连通分量的算法不太一样,关键是缺少\(num[](\text{很多大佬叫他dfn[]}),low[]\)。 但本质都是深搜,离线(算是吧),而且复杂度小得惊人。
关键是将搜过的节点合并到他的父亲节点上,很容易想到可以用并查集维护,时间复杂度极小。显然此时两节点的\(LCA\)就是最早合并的询问节点的父亲节点,这又是为什么呢?
你想啊,我们在搜索的时候,假设搜到了\(LCA\)节点我们会向一边搜索,然后回溯,搜索另一边,这时一定会到达另一询问点,由于并查集是回溯实现的,这时的父亲节点必是这两点的\(LCA\)。
当然我不会问你懂不懂,因为让我读这个大概或许读不懂,这是在模拟之后得出的经验,还有打表!
点我看大佬讲解(模拟)
放上面那个东西是因为太难写了!!
下面放下代码:
\(Code\):
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
struct edge
{
int to,nxt;
}e[500005<<1];
int head[500005],cnte=0;
void add_edge(int u,int v)
{
e[++cnte].to=v;
e[cnte].nxt=head[u];
head[u]=cnte;
}
struct node
{
int to,num,nxt;
}q[500005<<1];
int qu[500005],cntq=0;
void add_query(int u,int v,int k)
{
q[++cntq].to=v;
q[cntq].nxt=qu[u];
q[cntq].num=k;
qu[u]=cntq;
}
int f[500005];
void init(int n)
{
for(int i=1;i<=n;i++) f[i]=i;
return;
}
int getf(int u)
{
if(!(f[u]^u)) return f[u];
else return f[u]=getf(f[u]);
}
void merge(int u,int v)
{
int t1=getf(u),t2=getf(v);
if(t1^t2) f[t2]=t1;
return;
}
int vis[500005]={0},ans[500005]={0};
void dfs(int cur,int father)
{
for(int i=head[cur];i;i=e[i].nxt)
{
int j=e[i].to;
if(j^father&&!vis[j])
{
dfs(j,cur);
vis[j]=1;
merge(cur,j);
}
}
for(int i=qu[cur];i;i=q[i].nxt)
{
int j=q[i].to;
if(vis[j]) ans[q[i].num]=getf(j);
}
return;
}
int n,m,root;
int l,r;
int main()
{
scanf("%d%d%d",&n,&m,&root);
init(n);
for(int i=1;i<n;i++)
{
scanf("%d%d",&l,&r);
add_edge(l,r);
add_edge(r,l);
}
for(int i=1;i<=m;i++)
{
scanf("%d%d",&l,&r);
add_query(l,r,i);
add_query(r,l,i);
}
memset(ans,0,sizeof(ans));
dfs(root,root);
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
我知道你尝试看懂,但失败了(还是我都把你看成像我这样的蒟蒻了)
下面按分块的思想一一解决:
这里先给出有关变量、数组含义(大工程qwq):
struct edge
{
int to,nxt;
}e[500005<<1];
int head[500005],cnte=0;
这是前向星(邻接表结构体版)
struct node
{
int to,num,nxt;
}q[500005<<1];
int qu[500005],cntq=0;
用于存储询问。
对了,上面这俩要开二倍空间的(都是(类)无向图)
\(vis[]\):代表次点有没有被搜过,防止爆栈(其实是防T)
\(ans[]\):记录每个询问相对的答案
另外,出现了\(6\)个大大小小的函数:
void add_edge(int u,int v)
{
e[++cnte].to=v;
e[cnte].nxt=head[u];
head[u]=cnte;
}
前向星加边,假装都会吧。
void add_query(int u,int v,int k)
{
q[++cntq].to=v;
q[cntq].nxt=qu[u];
q[cntq].num=k;
qu[u]=cntq;
}
类似前向星的数据结构,将询问存入,支持按每个点相关遍历,将查找询问的\(O(q^2)\)优化成了\(O(q)\),仅仅将\(O(2q)\)的空间变成了\(O(7q)\),值了!
void init(int n)
{
for(int i=1;i<=n;i++) f[i]=i;
return;
}
int getf(int u)
{
if(!(f[u]^u)) return f[u];
else return f[u]=getf(f[u]);
}
void merge(int u,int v)
{
int t1=getf(u),t2=getf(v);
if(t1^t2) f[t2]=t1;
return;
}
并查集必备吧,假装都会了?
放篇不错的题解吧
void dfs(int cur,int father)
{
for(int i=head[cur];i;i=e[i].nxt)
{
int j=e[i].to;
if(j^father&&!vis[j])
{
dfs(j,cur);
vis[j]=1;
merge(cur,j);//注意这里是吧j合并到cur上,写反会WA
}
}
for(int i=qu[cur];i;i=q[i].nxt)
{
int j=q[i].to;
if(vis[j]) ans[q[i].num]=getf(j);
}
return;
}
对,这才是核心!
但我似乎并不知道从何讲起。
上半部分是把子节点遍历,下半部分是查找有关询问,记得控制\(vis[]\)数组。
这样,我们使用\(tarjan\)(太监) 算法,求\(LCA\)的时间复杂度就是\(O(n+q)\)了(\(n\)代表节点数,你也可以认为是边数,\(q\)是询问个数)。
\(ps\):我认为准确的复杂度是\(O(n\alpha(n)+q)\),不过不卡常可以认为是相等了。
再\(ps\)一下:有的大佬在存询问的结构体中设置记录该询问是否被回答的变量和记录相对空间的变量(就是记录那个询问存储与\(TA\)本质相同),其实都用处不大(跑满空间?),模拟后发现,在记录并判断\(vis[]\)的前提下,每个询问只会被回答\(1\)次,故这不多余(强者的世界我不懂,我还是算了吧)。
好了,似乎就这样讲完啦,理解背板子最重要呢(再回想下模拟过程?)。

