第一章 规划问题

第一章 规划问题

1.1 线性规划模型

1.1.1 基础numpy操作

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[1,2],[3,4],[5,6]])
c = np.array([[1,2,3]])
d = np.array([[9,8,7],[3,2,1]])

# 矩阵加法
sum = a + d
print(sum)

输出：[[10 10 10]
 	[ 7  7  7]]

# 放缩
e = 3*a
print(e)

输出：[[ 3  6  9]
 	[12 15 18]]

# 数乘、矩阵乘
e = np.dot(a,b)
print(e)

输出：[[22 28]
 	[49 64]]

# 元素乘
e = a*d
print(e)

输出：[[ 9 16 21]
 	[12 10  6]]

# 转置
e = c.T
print(e)

输出：
[[1]
 [2]
 [3]]

e = np.array([[1,2],[3,4]])
# 逆矩阵
result = np.linalg.inv(e)
print(result)

输出：
[[-2.   1. ]
 [ 1.5 -0.5]]

# 行列式
result = np.linalg.det(e)
print(result)

输出：-2.0000000000000004

# 矩阵的秩
e = np.linalg.matrix_rank(d)
print(e)

输出;2

1.1.2 例题1（标准形式）

以上为基础的矩阵操作功能，接下来我们队一道题目进行解答.

例题：

\(\left\{\begin{aligned} 10 x-y-2 z &=72 \\-x+10 y-2 z &=83 \\-x-y+5 z &=42 \end{aligned}\right.\)

import numpy as np

A = np.array([[10,-1,-2],[-1,10,-2],[-1,-1,5]]) # A为系数矩阵
b = np.array([72,83,42]) # b为常数列
inv_A = np.linalg.inv(A) #A的逆矩阵
x = np.dot(A,b) # A的逆矩阵与b做点积运算
x = np.linalg.solve(A,b) # 5,6两行也可用本行替代
print(x)

[11. 12. 13.]

使用 sympy 进行解答

from sympy import symbols,Eq,solve

x,y,z = symbols('x,y,z')
eqs = [Eq(10*x - y - 2*z, 72),
       Eq(-x + 10*y - 2*z, 83),
       Eq(-x - y + 5*z, 42)]
print(solve(eqs,[x,y,z]))

{x: 11, y: 12, z: 13}

sympy 主要用于符号解，numpy 和 scipy 主要用于数值解

1.1.3 例题2（不等式形式）

\(\max \quad z=2 x_{1}+3 x_{2}-5 x_{3}\)
s.t. \(\left\{\begin{array}{l}x_{1}+x_{2}+x_{3}=7 \\ 2 x_{1}-5 x_{2}+x_{3}>=10 \\ x_{1}+3 x_{2}+x_{3}<=12 \\ x_{1}, x_{2}, x_{3}>=0\end{array}\right.\)

from scipy import optimize
import numpy as np

c = np.array([-2,-3,5])
A = np.array([[-2,5,-1],[1,3,1]])
b = np.array([-10,12])
Aeq = np.array([[1,1,1]])
beq = np.array([7])
x1 = (0,None)
x2 = (0,None)
x3 = (0,None) # 指的是x1,x2,x3的范围为 0 到无穷大

res = optimize.linprog(-c,A,b,Aeq,beq,bounds=(x1,x2,x3))
print(res)
print(res.x)

     con: array([1.52631917e-07])
     fun: -14.000000657683213
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([-4.30601379e-07,  5.00000013e+00])
  status: 0
 success: True
       x: array([2.99999979e+00, 1.04988686e-08, 4.00000005e+00])
[2.99999979e+00 1.04988686e-08 4.00000005e+00]

fun 为最小值, slack 为精度, x 为对应的变量值,可以通过 res.xxx 来显示对应的内容。

1.2 非线性规划

例题

【列 3-1】三台火电机组的运行成本 (单位: \(t / h\) ) 与出力限㓡 (单位：MW) 分别如下:

\[\left\{\begin{array}{l} F_{G 1}=4+0.3 P_{G 1}+0.0007 P_{G 1}^{2}, 100 \leqslant P_{G 1} \leqslant 200 \\ F_{G 2}=3+0.32 P_{G 2}+0.0004 P_{G 2}^{2}, 120 \leqslant P_{G 2} \leqslant \leqslant 250 \\ F_{G 3}=3.5+0.3 P_{G 3}+0.00045 P_{G 3}^{2}, 150 \leqslant P_{G 3} \leqslant 300 \end{array}\right. \]

当负荷为 \(700 \mathrm{MW}\) 时, 求经济调度的结果。
下面我们分别用scipy和遗传算法求解。

解法1（scipy）

可以选择对应的插值方式

from scipy.optimize import minimize
import numpy as np
# 目标函数即min(FG1+FG2+FG3)
def fun(x):
    return (4+0.3*x[0]+0.0007*x[0]*x[0]+3+0.32*x[1]+0.0004*x[1]*x[1]+3.5+0.3*x[2]+0.00045*x[2]*x[2])

def con():
    # 约束条件分别为eq和ineq
    # eq表示函数结果等于0；ineq表示表达式大于或等于0
    cons = ({'type':'eq','fun':lambda x:x[0]+x[1]+x[2]-700})
    # {'type':'ineq','fun':lambda x: -x[2] + x - max} 如果有不等式约束
    # cons = ([con1,con2,con3,con4,con5,con6,con7,con8]) 如果与多个约束，最后返回结果是这个
    # x[0] 其中的0必须是具体数字，不能是t等参数
    return cons

# 上下限约束
b1 = (100,200)
b2 = (120,250)
b3 = (150,300)
bnds = (b1,b2,b3) # 边界约束
if __name__ == "__main__":
    cons = con() # 约束
    # 设置x初始猜测值
    x0 = np.array((150,250,20))
    res = minimize(fun,x0,method = "SLSQP",constraints=cons,bounds=bnds)	# method可选
    print("结果",res.fun)
    print(res.success)
    print("解",res.x)
    print(res)
    
    
输出：
结果 305.96739130656937
True
解 [176.08556664 250.         273.91443336]
     fun: 305.96739130656937
     jac: array([0.54652023, 0.52000046, 0.54652405])
 message: 'Optimization terminated successfully'
    nfev: 32
     nit: 8
    njev: 8
  status: 0
 success: True
       x: array([176.08556664, 250.        , 273.91443336])

解法2（遗传算法）

通常是一个近似解

from sko.GA import GA

def fun(x):
  return(4+0.3*x[0]+0.0007*x[0]*x[0]+3+0.32*x[1]+0.0004*x[1]*x[1]+3.5+0.3*x[2]+0.00045*x[2]*x[2])

def cons1(x):
    return [x[0]+x[1]+x[2]-700]
cons = cons1

ga = GA(func=fun,n_dim = 3,size_pop=200,max_iter=800,lb=[100,120,150],ub=[200,250,300],constraint_eq=[cons])
best_x,best_y=ga.run()
print("best_x:",best_x,"\n","best_y:",best_y)


输出：
best_x: [195.39379114 238.51964394 266.08656494] 
best_y: [306.61308165]

1.3 整数规划模型

例题

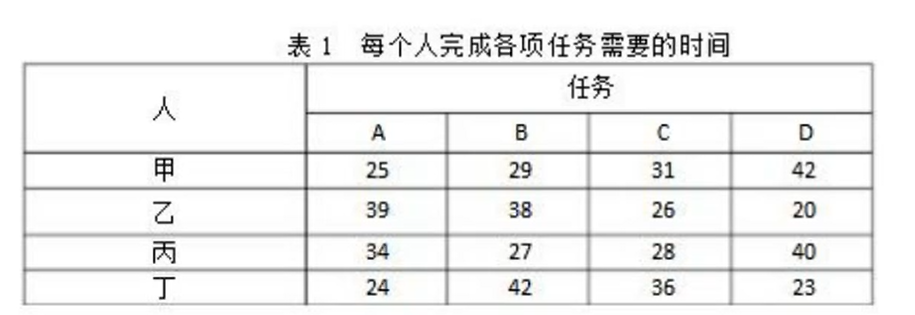
假设有四件事四个人去做，各变量对应的数据假设如表所示

from scipy.optimize import  linear_sum_assignment
import numpy as np

cost = np.array([[25,29,31,42],[39,38,26,20],[34,27,28,40],[24,42,36,23]])
row_ind,col_ind = linear_sum_assignment(cost)  # 默认求最小，如需求最大可在后添加 True

print(row_ind)  # 开销矩阵对应的行索引
print(col_ind)  # 对应行索引的郋指派的列索引
print(cost[row_ind,col_ind])    # 提取每个行索引的最有指派列索引的元素，形成数组
print(cost[row_ind,col_ind].sum())  # 数组求和


输出：
[0 1 2 3]
[0 2 1 3]
[25 26 27 23]
101

1.4 动态规划模型

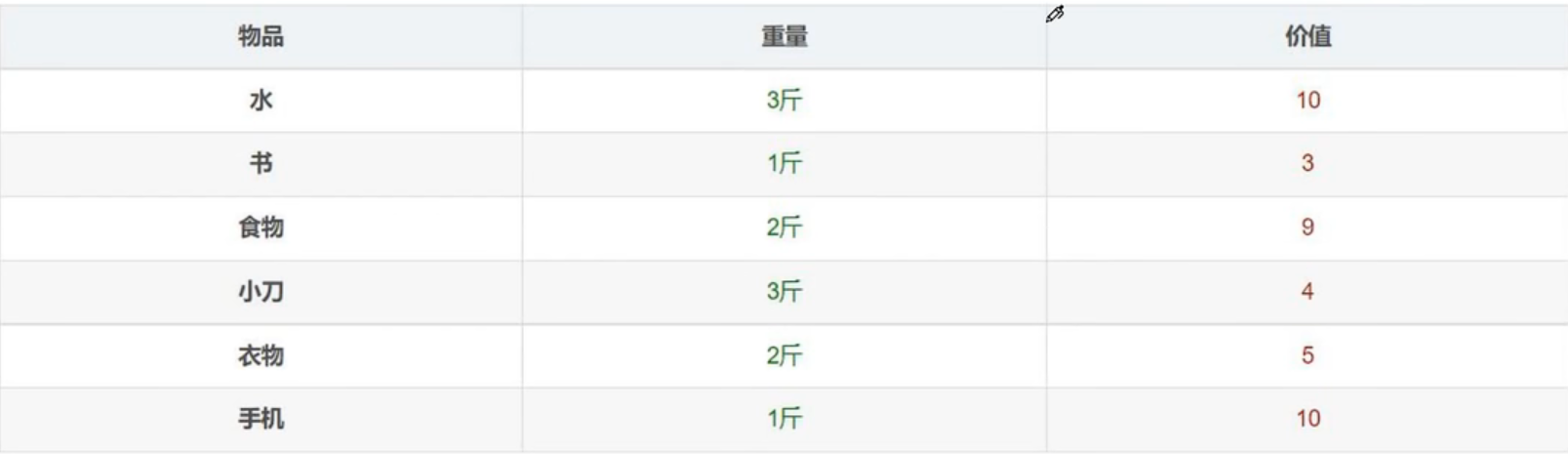
例题

解答：

def dynamic_p() -> list:
    items = [
        {"name":"水","weight": 3,"value":10},
        {"name": "书", "weight": 1, "value": 3},
        {"name": "食物", "weight": 2, "value": 9},
        {"name": "小刀", "weight": 3, "value": 4},
        {"name": "衣物", "weight": 2, "value": 5},
        {"name": "手机", "weight": 1, "value": 10}
    ]

    max_capacity = 6
    dp = [[0] * (max_capacity + 1) for _ in range(len(items) + 1)]

    for row in range(1,len(items) + 1 ):
        for col in range(1,max_capacity + 1):
            weight = items[row - 1]["weight"]
            value = items[row - 1]["value"]
            if weight >col:
                dp[row][col] = dp[row - 1][col]
            else:
                dp[row][col] = max(value + dp[row-1][col - weight],dp[row - 1][col])
    return dp

dp = dynamic_p()
for i in dp:
    print(i)

print(dp[-1][-1])



输出：[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 10, 10, 10, 10]
[0, 3, 3, 10, 13, 13, 13]
[0, 3, 9, 12, 13, 19, 22]
[0, 3, 9, 12, 13, 19, 22]
[0, 3, 9, 12, 14, 19, 22]
[0, 10, 13, 19, 22, 24, 29]

P.S. 详细的动态规划内容可以参照博客内leetcode中的动态规划专题