Vectors, what even are they?

Interpretations of Vectors

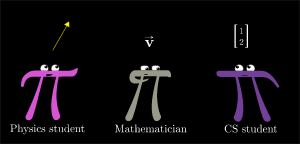
• Physics Perspective：vectors are arrows pointing in space.

• CS Perspective:vectors are ordered lists of numbers.

• Mathematician's Abstraction:vector can be anything where there’s a sensible notion of adding two vectors and multiplying a vector by a number.

\[\begin{gathered} {\left[\begin{array}{c} 3 \\ -5 \end{array}\right]+\left[\begin{array}{l} 2 \\ 1 \end{array}\right]=\left[\begin{array}{c} 3+2 \\ -5+1 \end{array}\right]} \\ 2\left[\begin{array}{c} 3 \\ -5 \end{array}\right]=\left[\begin{array}{c} 2(3) \\ 2(-5) \end{array}\right] \end{gathered} \]

Thinking About Coordinate Systems

Two dimensions:

• x-axis:a horizontal line
• y-axis:a vertical line

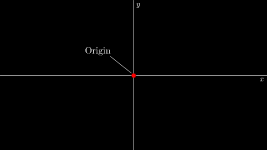
Origin:The place where they intersect,as the center of space and the root of all vectors.

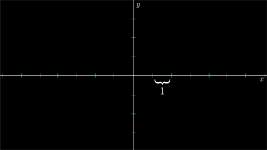
Choosing an arbitrary distance to represent a length of 1

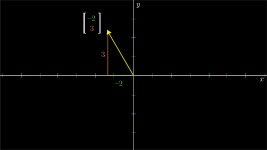
The coordinates of a vector are a pair of numbers that basically give instructions for how to get from the tail of that vector at the origin,,to its tip.

• The first number:how far to walk along the x-axis

  • positive numbers indicating rightward motion
  • negative numbers indicating leftward motion.

• the second number:how far to then walk parallel to the y-axis.

  • positive numbers indicating upward motion
  • negative numbers indicating downward motion.

To distinguish vectors from points, the convention is to write this pair of numbers vertically with square brackets around them.\(\nwarrow=\left[\begin{array}{c}-2 \\ 3\end{array}\right] \neq(2,3)\)

Every pair of numbers gives you one and only one vector, and every vector is associated with one and only one pair of numbers.【每一对数给出唯一的一个向量，每一个向量对应唯一的一个数。】

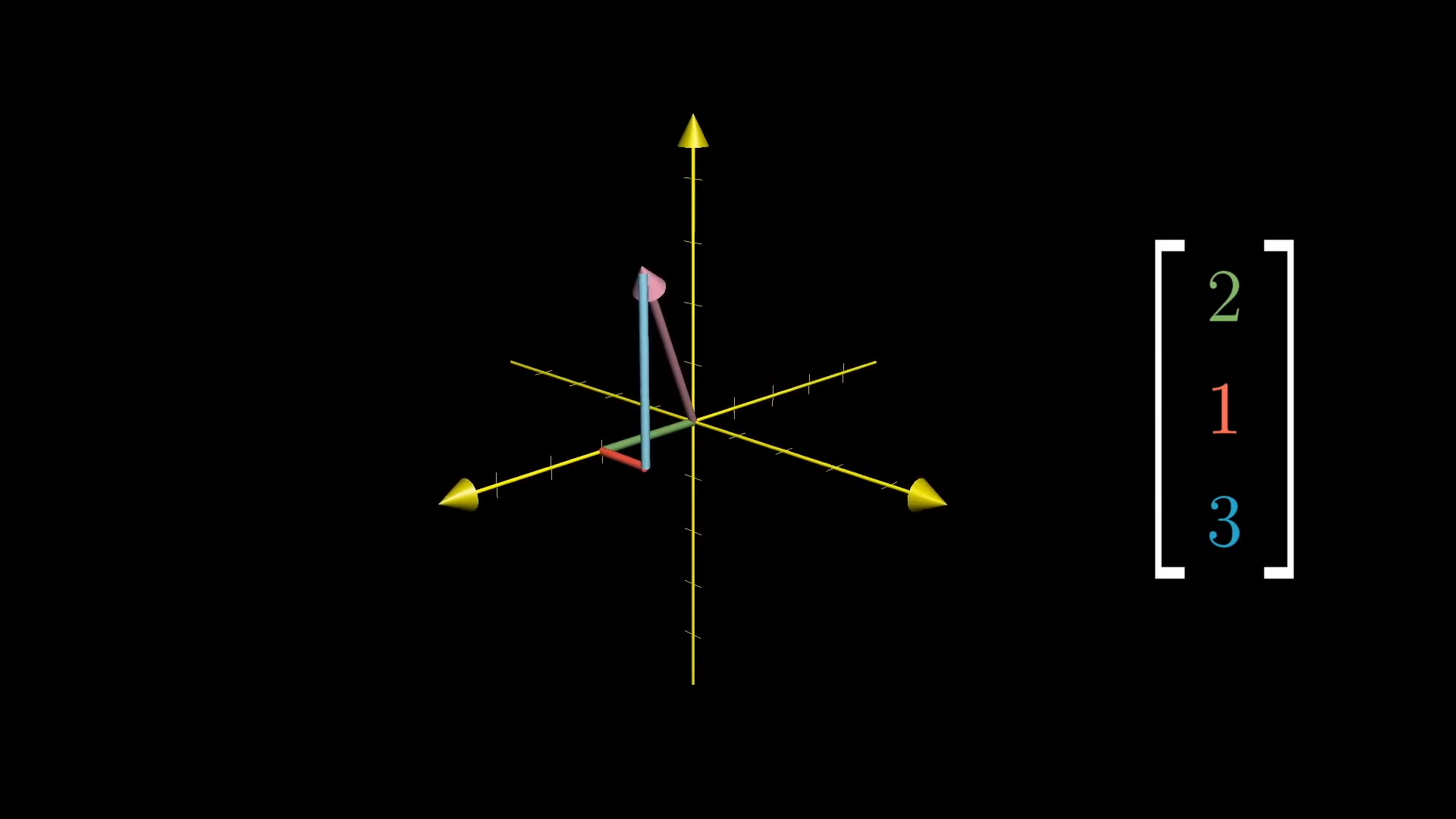
In three-dimensions：

• z-axis：perpendicular to both the x and the y axes.

Each vector is associated with an ordered triplet of numbers.

• The first number:how far to move along the x-axis;

• The second number :how far to move parallel to the y-axis;

• The third number:how far to move parallel to the new z-axis.

Every triplet of numbers gives you one unique point in space, and every point in space is associated with exactly one triplet of numbers.【每一对三元组给出空间中唯一的一个点，每一个空间中的点对应唯一的一对三元组。】

Vector Operations

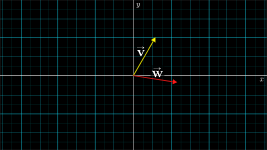
Addition

We have two vectors, one pointing up and a little to the right, and another pointing to the right and a little bit down.

1. Move the second vector so that it’s tail sits on the tip of the first one.

2. Draw a new vector from the tail of the first one to where the tip of the second now sits.

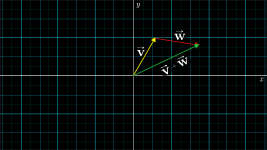
Two perspectives on vector addition：

• Each vector represents a certain movement:a step with a certain distance and direction.

  • take a step along the first vector, then take a step along the second vector \(\Rightarrow\) move along the sum of those two vectors.

• Add numbers on a number line.

  • move \(2\) steps to the right,followed by another \(5\) steps to the right \(\Rightarrow\) move \(7\) steps to the right to begin with.

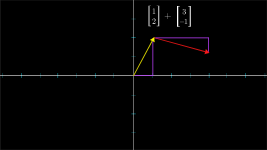
Numerical effect：The first vector here has coordinates \(\left[\begin{array}{l}1 \\ 2\end{array}\right]\)，, and the second has coordinates \(\left[\begin{array}{c}3 \\ -1\end{array}\right]\)

Take vector sum \(\Rightarrow\) a four step path from the tail of the first to the tip of the second:

1. Walk \(1\) to the right;
2. Walk \(2\) up;
3. Walk \(3\) to the right;
4. Walk \(1\) down.

\(\Leftrightarrow\) first do all the rightward motion, then all the vertical motion:

1. Move \(1+3\) to the right;
2. Move \(2-1\) up.

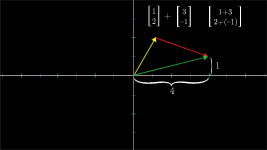
Addition of vectors:Add two vectors means match up their terms and add them each together( in the list-of-numbers conception of vectors ).

\[\left[\begin{array}{l} x_1 \\ y_1 \end{array}\right]+\left[\begin{array}{l} x_2 \\ y_2 \end{array}\right]=\left[\begin{array}{l} x_1+x_2 \\ y_1+y_2 \end{array}\right] \]

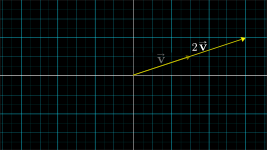
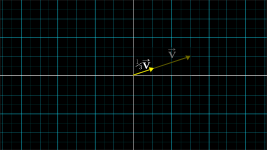
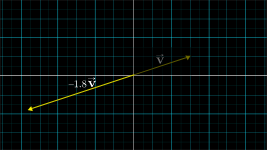
Scaling

\(2 \overrightarrow{\mathbf{v}}\)
\(\frac{1}{3} \overrightarrow{\mathbf{v}}\)
\(-1.8 \overrightarrow{\mathbf{v}}\)

• This process of stretching, squishing, and sometimes reversing direction, is called “scaling”.
• Whenever you catch a number like \(2\), \(\frac{1}{3}\), \(-1.8\) acting like this, scaling some vector, is called “scalar”.

Multiplication of vectors：multiplying a given vector by a scalar means multiplying each one of its components by that scalar.

\[a \overrightarrow{\mathbf{v}}=a \cdot\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} a x \\ a y \end{array}\right] \]

Conclusion

**Every linear algebra topic revolves around these two fundamental operations of vector addition and scalar multiplication.【每个线性代数主题都围绕向量加法和标量乘法这两个基本运算展开。】 **

\[\nearrow \Rightarrow\left[\begin{array}{l} 2 \\ 1 \end{array}\right] \Rightarrow \nearrow \]

The usefulness of linear algebra has less to do with either one of these views than it does with the ability to translate back and forth between them.

1. It gives the data-analyst a nice way to conceptualize many lists of numbers in a visual way, which can seriously clarify patterns in the data and give a global view of what certain operations do.

2. On the flip side, it gives people like physicists and computer graphics programmers a language to describe space, and the manipulation of space, using numbers that can be crunched and run through a computer.