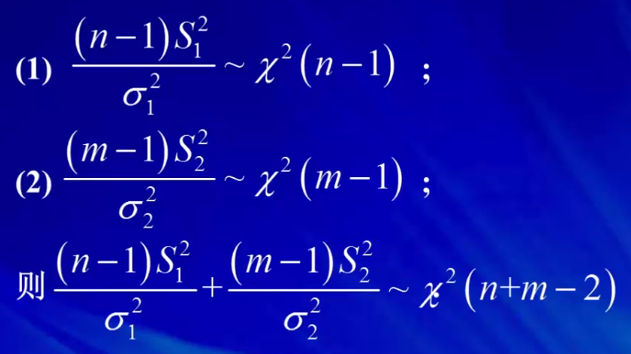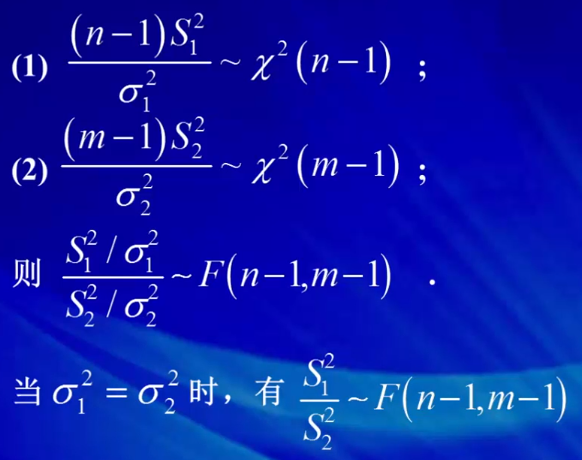S&p_11_数理统计
数理统计
1. 数理统计:就是未知总体分布,利用样本信息推断出总体分布或总体参数,是概率论研究的源头。(而概率论是已知总体分布,通过计算来的出x函数的期望和方差)
2. 统计量:统计量是样本的函数,且统计量不能包含任何总体分布中未知的参数。所以说一旦有了样本观测值后,统计量就是确定下来,是一个已知的值。

2)中有未知参数u。1)和3)没有未知参数,而只是样本函数,所以都是统计量。


Xi为样本中第i个个体,因为在观测前是不确定的,它是一个随机变量,而 xi 为第i个个体样本的观测值。样本均值相当于样本的一阶原点矩。
同样,S^2为样本方差,,而s^2为样本的观测值的方差。S与Sn之间的区别是系数1/n-1与1/n,其中S为样本的中心矩,而Sn为样本方差/标准差等。
样本的原点矩和中心矩,系数都是1/n。而只有样本的方差/标准差的系数为1/n-1.


其中,Σ(1~n)Xi = n*X_bar(X的平均值)。

3. 统计量的性质


随机变量之和的期望为u,E(n*X_bar) =nu,所以E(X_bar) = u。
随机变量之和的方差,因为独立,它的方差等于方差之和为n*Signma平方。由于Σ(1~n)Xi (随机变量之和)= n*X_bar,所以D(ΣXi) = D(n*X_bar) = n^2*D(X_bar) = n*σ^2。所以D(X_bar) = σ^2/n。
统计量的性质与结论:
E(X) = u, E(ΣXi) = nu, E(X_bar)=u, E(S2) = 1/n Σ E(Xi-X_bar)2 = 1/n Σ E(Xi2-X_bar2) =(D(x1) + E(X1)2 - D(X_bar) - E(X_bar)2) = σ2
D(X) = E(x2-E(x)2) = σ2, D(ΣXi) = E(Σxi2-E(x_bar)2) = nσ2, D(X_bar)= σ2/n, D(S2) = 2σ4/n-1
4. 统计常见分布
统计学上,自由度是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的数据的个数,称为该统计量的自由度。一般来说,自由度等于独立变量减掉其衍生量数。举例来说,变异数的定义是样本减平均值(一个由样本决定的衍生量),因此对N个随机样本而言,其自由度为N-1。
卡方分布:Xi独立同分布,且服从正太分布,那么Xi2求和就是卡方分布,即Y~X2(n)。


X12~X2(1)表示X12服从自由度为1的卡方分布,X22~X2(1)表示X22服从自由度为1的卡方分布,X12+X22~X2(2)表示X12+X22服从自由度为2的卡方分布. 自由度意思是样本中独立或能自由变化的数据的个数,由于X1和X2是独立同分布,这样它们自由度相互不受约束。

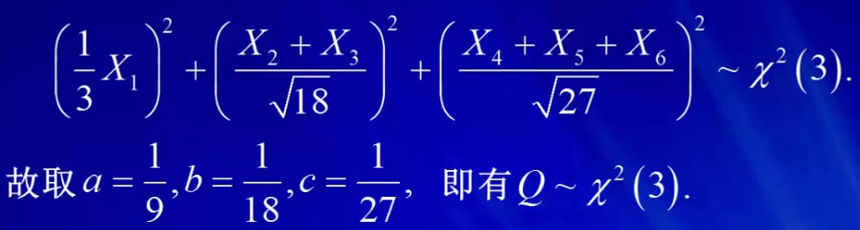
当我们要构造卡方分布时,必须是标准正态分布才有资格平方求和。一般的正态分布是很容易通过标准化,把它转化成标准正态分布的。
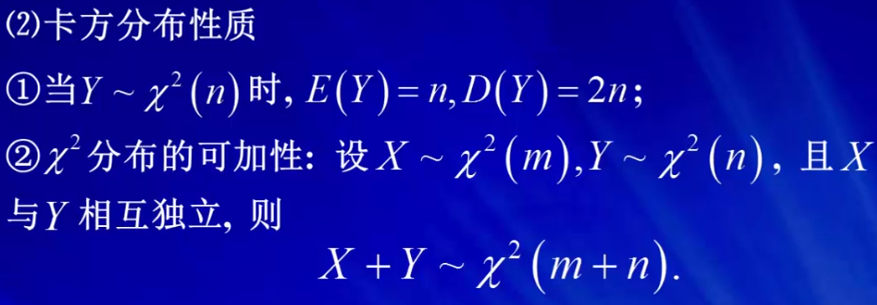
X~X2(n)时,E(X_bar) = E(X) =n;D(X_bar) = 2, D(x) = 2n
T分布:将卡方分布放在分子,并除以自由度,而将正态分布放在分母,就得到了t分布。


t分布与正态分布的密度函数图像很相似,都是以Y轴为对称轴的倒中型。

F分布是把两个自由度为m和n的卡方分布,分别放在分子和分母,并且除以他们各自的自由度,那么这样的表达式就服从F分布。



F分布的性质:

1. 数理统计
1.1 样本
概率论的研究,常常假设概率论已知,去计算概率。讨论分布或数字特征的一些性质。但在实际问题中,情况往往相反,一个随机变量服从什么样的分布可能完全不知道。
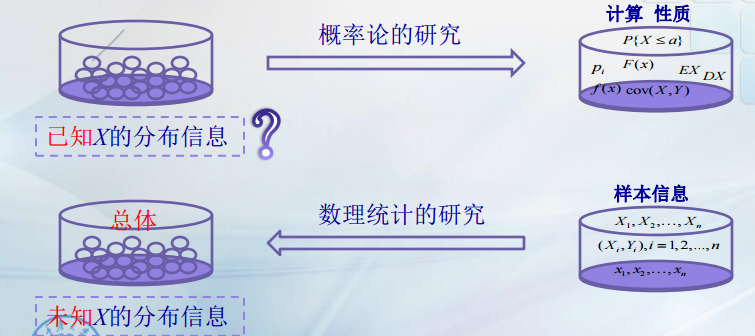
数理统计就是利用样本信息去推断总体分布或总体参数,是概率论研究的源头,也是一个思维归纳的过程。
例子
- 车辆的行驶速度服从正态分布, Γ分布还是指数分布?
- 城市里65岁以上老年人的 比例 p是多少呢?(这个问题服从两点分布,但不知道比例P)
怎样才能知道一个随机变量的分布或其参数呢?这是数理统计要解决的首要问题。
就上面的例子而言,我们必要对其进行观测,取得信息,对其分布做出推断。由于每次观测是随机现象,那么对有限的观测对整体做出推断是不可能做到绝对准确的,所以我们用概率来度量其可靠性。数理统计就是研究统计推断方法,每个推断便随一定的概率以表明推断的可靠性。数理统计就是研究统计推断方法。每个推断伴随一定的概率,以表明推断的可靠程度。


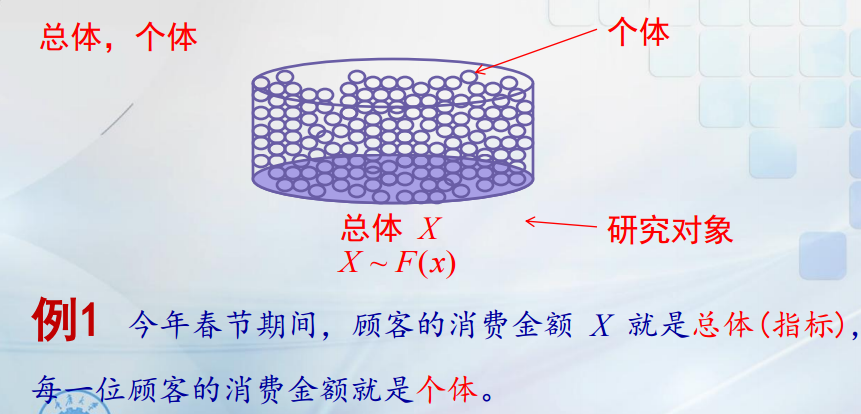
总体和个体都是数据,在数理统计中,我们将研究的的对象所构成的集合称为总体。而个体则是每个随机变量的值。
我们可以通过观测,从总体中抽取的部分个体称为样本。即n个个体指标 记为X1,X2,Xn ,其中n是样本容量。



X为n为随机变量,x为简单随机样本,即具体数据。





离散型:


X1,X2,...,Xn离散随机变量的联合概率函数:f*(x1,x2,..,xn)= P(X1=x1)*P(X2=x2)*……P(Xn=xn) 为每个个体的概率值的乘积。

连续型:


X1,X2,...,Xn 连续随机变量的联合概率函数:f*(x1,x2,..,xn)= fx1(x1)*fx2(x2) 为每个个体的概率值的乘积。


总体的分布未知,从总体里抽样,抽样之后我们得到样本,有了样本我们就进行观测,从而得到样本值,在通过样本值对总体的分布进行推断。
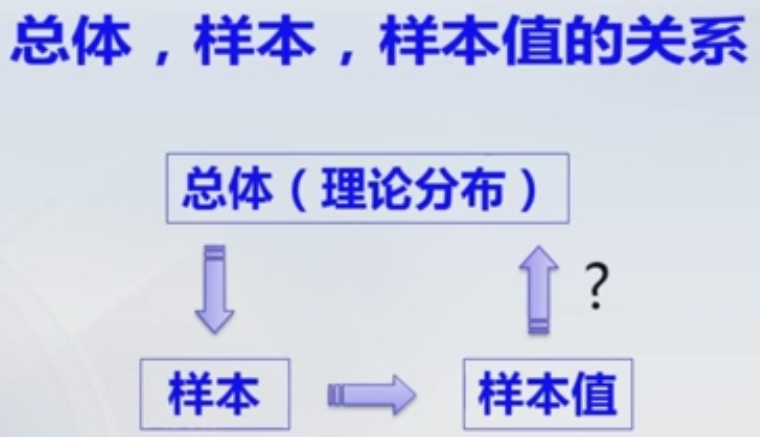
由于样本是从总体中抽取出来的,因此样本的统计规律性与总体的统计规律性之间有密切的关系。

怎么认识总体分布? 我们可以根据样本信息,利用图形来直观的描述样本观测值的分布特征。一般用经验分布函数刻画分布函数,而用直方图描述其密度函数。例子如下:
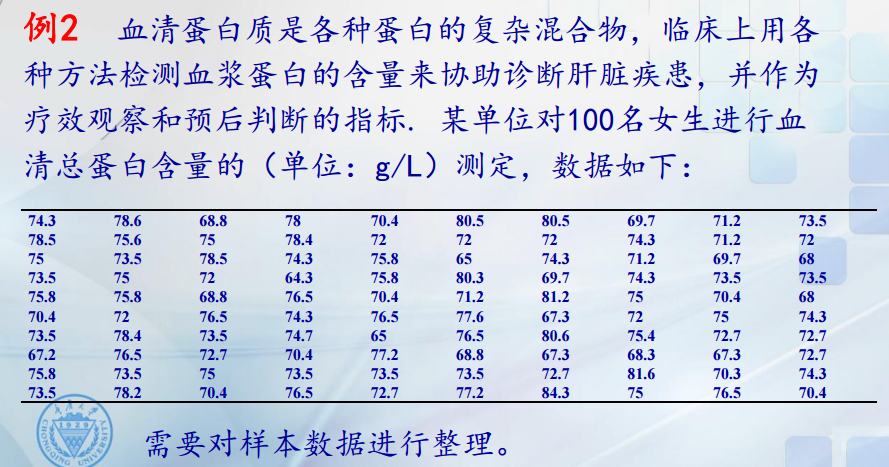

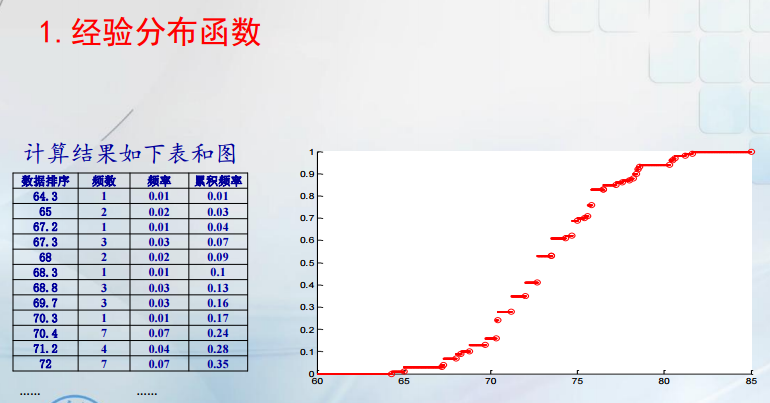

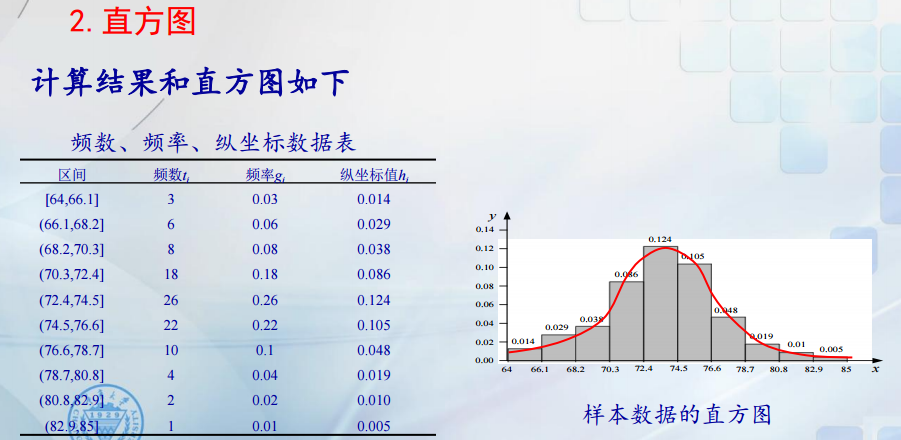
除了对样本数据进行描述以外,我们还可以构造样本函数,它能刻画总体的数字特征,如均值,方差等。
1.2 统计量
![]()
统计量是样本的函数,且统计量不能包含任何总体分布中,未知的参数。所以说一旦有了样本观测值后,统计量就是确定下来,是一个已知的值。

2)中有未知参数u,所以不是统计量。1)和3)没有未知参数,而只是样本函数,所以都是统计量。


Xi为样本中第i个个体,因为在观测前是不确定的,它是一个随机变量,而 xi 为第i个个体样本的观测值。样本均值相当于样本的一阶原点矩。
同样,S^2为样本方差,,而s^2为样本的观测值的方差。S与Sn之间的区别是系数1/n-1与1/n,其中S为样本的中心矩,而Sn为样本方差/标准差等。
样本的原点矩和中心矩,系数都是1/n。而只有样本的方差/标准差的系数为1/n-1.


其中,Singma(1~n)Xi = nX_bar(X的平均值)。


样本中的下标不带括弧,Xi表示第i个个体,带括号表示次序统计量。
1.3 常用统计量的性质


- 样本均值和样本方差主要刻画主体分布的中心位置和偏离中心的程度。
- 中位数和极差也同样可以刻画主体分布的中心位置。 只是用在不同的情况下。


- 当样本容量n趋于无穷时,样本均值和方差依概率收敛于总体均值和总体方差。即当n足够大,样本均值和方差可以用于估计总体均值u和方差Sigma平方。
- 样本均值的期望和方差分别为总体期望u和n分之Sigma平方,这表明n越大样本均值的方差越小,波动越小。
- 样本方差的期望和方差分别为总体方差Sigma平方和n-1分之2倍Sigma四次方。


随机变量之和的期望为u,E(n*X_bar) =nu,所以E(X_bar) = u。
随机变量之和的方差,因为独立,它的方差等于方差之和为n*Signma平方。由于Σ(1~n)Xi (随机变量之和)= n*X_bar,所以D(ΣXi) = D(n*X_bar) = n^2*D(X_bar) = n*σ^2。所以D(X_bar) = σ^2/n。
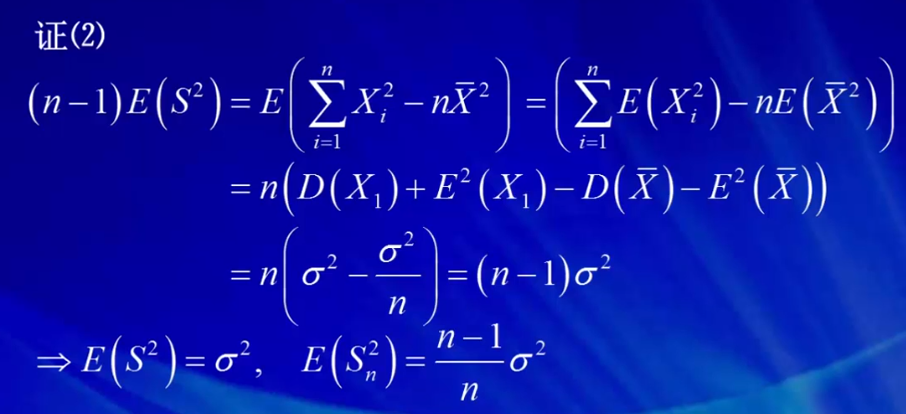
- Σ(Xi - X_bar)2 = ΣXi2 - 2X_bar*ΣXi + nX_bar2 =ΣXi2 - nX_bar2
- D(Xi) = E(Xi2 - E(xi)2)
- 随机变量线性函数的期望=期望的线性函数:E(f(x)) = f(E(x)), 即E(ΣXi) = Σ(E(xi))
- 由于每个随机变量Xi是同分布的,所以Xi^2期望求和,可以改写成其中某个个体的期望的n倍:E(ΣXi) = Σ(E(xi))
- 又由于Xi和X_bar,两个随机变量的期望和方差都有已知的结论,所以我们用随机变量平方的期望等于随机变量的方差+随机变量期望的平方:即E(X^2) = D(X) + (E(X))^2
- 最后将E(x)=u,D(x)=σ^2,E(X_bar)=u,D(X_bar)=σ^2/n代入公式



1.4 统计常用分布(卡方分布,t分布,F分布)
统计学上,自由度是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的数据的个数,称为该统计量的自由度。一般来说,自由度等于独立变量减掉其衍生量数。举例来说,变异数的定义是样本减平均值(一个由样本决定的衍生量),因此对N个随机样本而言,其自由度为N-1。


X12~X2(1)表示X12服从自由度为1的卡方分布,X22~X2(1)表示X22服从自由度为1的卡方分布,X12+X22~X2(2)表示X12+X22服从自由度为2的卡方分布. 自由度意思是样本中独立或能自由变化的数据的个数,由于X1和X2是独立同分布,这样它们自由度相互不受约束。
![]()

卡方分布的密度函数图形是一个偏峰的倒U型。


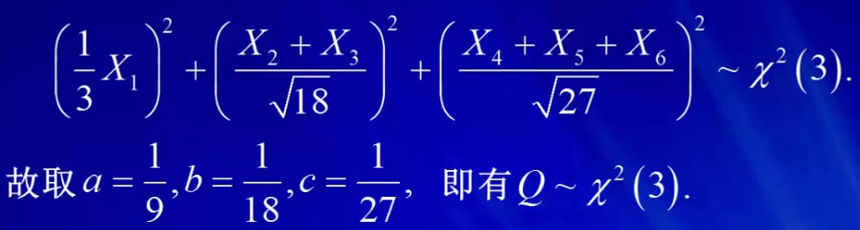
由于正态分布的性质,已知X1~N(0,9),X1服从0,9的正态分布,那么标准化1/3X1~N(0,1),标准化1/3X1服从0,1的正态分布。
由独立正态分布的可加性,X2+X3~N(0,18),X2和X3相加服从0,18的正态分布,那么X2和X3相加/square(18),服从标准正态分布。
同理,X4+X5+X6/square(27) 服从标准正态分布。这样就有1/3X1,X2+X3/square(18),X4+X5+X6/square(27) 相互独立且同分布,所以我们才可以由卡方分布的定义,它们的平方和,服从自由度为3的卡方分布。
得系数a=1/9,b=1/18,c=1/27。从这个例子中,告诉我们当我们要构造卡方分布时,必须是标准正态分布才有资格平方求和。
一般的正态分布是很容易通过标准化,把它转化成标准正态分布的。
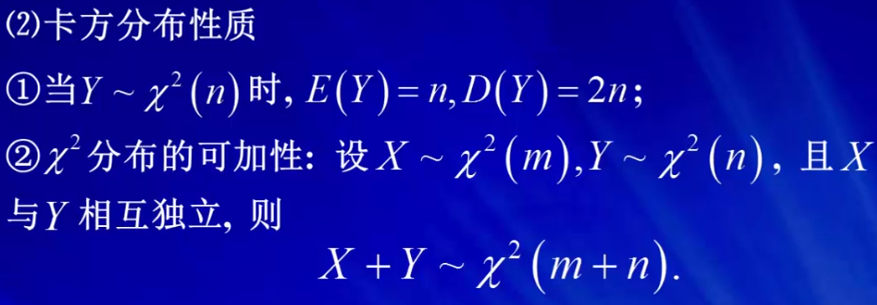


1)X服从正态分布,所以D(X)=1,E(x)=0,所以最终E(Y) = n
E(X^4) = 3, E(X^2)=1

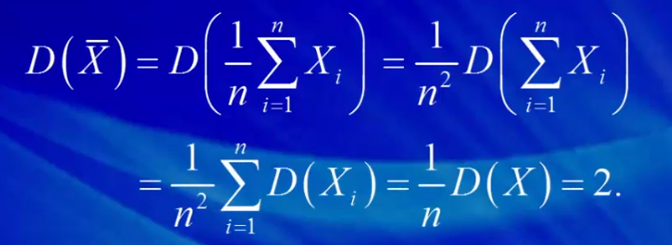
E(X_bar) = E(X) =n
D(X_bar) = 2, D(x) = 2n
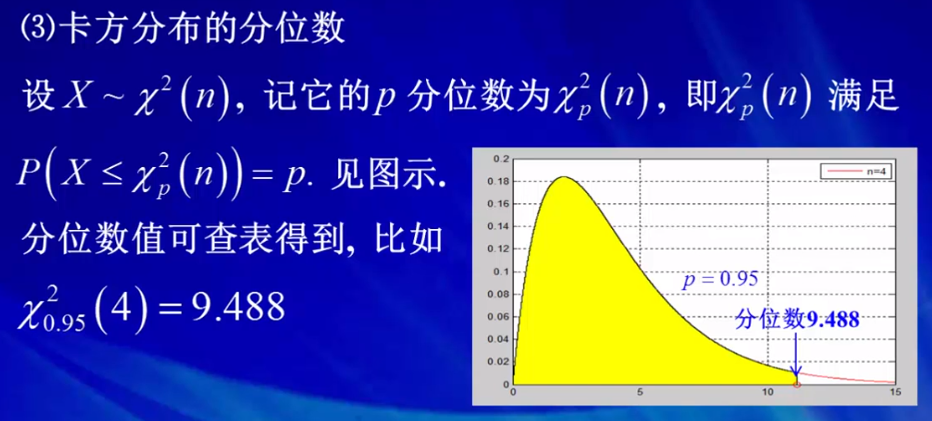
X20.95(4) = 9.488,表示一个自由度为4的卡方分布,它小于9.488的概率等于0.95。
T分布


将卡方分布放在分子,并除以自由度,而将正态分布放在分母,就得到了t分布。

t分布与正态分布的密度函数图像很相似,都是以Y轴为对称轴的倒中型。



Xi是相互独立的正态分布,X32+X42+X52服从自由度为3的卡方分布,而正态分布的可加性,X1+X2服从参数为0,2的正态分布,X32+X42+X52与X1+X2是相互独立的,其中X1+X2不是标准正态分布,得先标准化,再将其放入分子作为t分布的一个部分,构成一个服从自由度为3的t分布。。

自由度为10的t分布,这个随机变量小于1.812的概率等于0.95. 同时这个随机变量小于-1.812的概率为0.05.
F分布


F分布是把两个自由度为m和n的卡方分布,分别放在分子和分母,并且除以他们各自的自由度,那么这样的表达式就服从F分布。

F分布的概率密度函数图形,也是一个偏峰的到U型。

其中X12和X22服从自由度为2的卡方分布,X32+X42+X52服从自由度为3的卡方分布,因为这里的两个变量和是相互独立,所以这个公式服从第一自由度为2,第二自由度为3的F分布。


它表示我们有一个随机变量服从第一自由度为m,第二自由度n的F分布,那么它小于Fp的概率是P
F分布的性质,只要将F取倒数,这他们的自由度就对调。

2. 正态总体的抽样分布

2.1 单正态总体的抽样分布。
在正态总体的抽样分布中,要熟悉标准化的过程,因为构造3大分布时,需要先转化成标准正态分布。






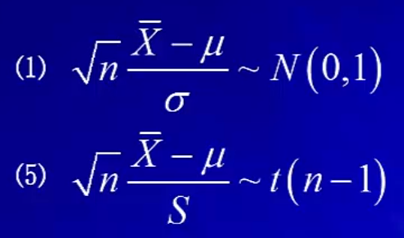
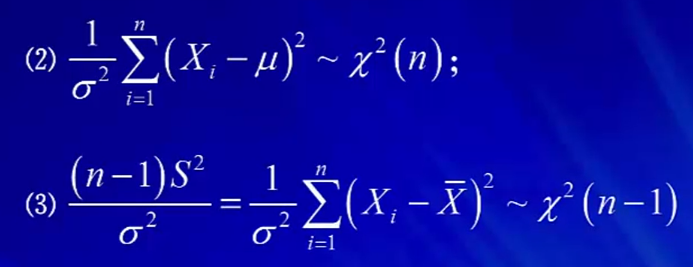



2.2 双正态总体的抽样分布