S&p_10_大数定律与中心极限定理
极限定理
1. 依概率收敛:依概率收敛与数理收敛不一样:在高度数学中,数列Xn的极限为C,它的定义方式:当n充分大时,Xn与C之间的距离任意的小,即|Xn-C|<Epsilon,n->无穷大。而随机变量Xn的极限时C,当n充分大时,Xn与C的距离任意小。这是错的。(例如,投n次硬币,全是正面朝上,这样的概率存在,且为1/2^n。所以不能说Xn与C的距离任意小,而只能说依概率,频率和0.5之间出现较大的偏差的可能性的极限为0,并会与0.5非常接近。)当n趋向于无穷大时,它的概率收敛到0。通过证明我们可以得到,频率和0.5之间出现较大的偏差的可能性的极限为0。当n充分大时,两者任意接近的可能性为1。在概率的意义上就保证了极限为0.5,此时称依概率收敛到0.5.
2. 大数定律:随着试验次数的增大,这个频率趋于真实概率的可能性趋于1。大数定律讲的是,样本容量极大时,样本的均值必然趋近于总体的期望。
三个大数定律的关系:
-
- 切比雪夫大数定律:它要求随机变量两两不相关,并且方差是有界的。
- 独立同分布的大数定律:它要求随机变量独立同分布,并且每个随机变量的期望和方差都存在。它是切比雪夫大数定律的特例。
- 贝努利大数定律:它不仅要求随机变量独立同分布,还要求每个变量都服从两点分布。它是独立同分布大数定律的特例。
3. 中心定理:多重随机变量独立且服从0-1分布,当n趋向于无穷大是,多重随机变量联合分布服从正态分布。中心极限定理讲的是:样本容量极大时,样本均值的抽样分布趋近于正太分布。这和样本所属的总体的分布的类型无关,样本所属总体的分布可以是正态分布,也可以不是。(由随机变量序列的和的分布近似于正态分布这个定理,当随机变量序列Xi的分布未知,如果n趋向于很大(无穷大),那么可以利用随机变量序列和的分布来求解。)
4. 中心定理推广:多重随机变量独立同分布,当n趋向于无穷大是,多重随机变量联合分布服从正态分布。
中心极限定理代码:https://www.cnblogs.com/tlfox2006/p/10001242.html
大数定理和中心极限定理的区别
https://www.zhihu.com/question/22913867
1. 大数定律
引例 灯泡寿命估计
现有一批来自同一生产线的同型号 灯泡,每只灯泡的寿命服从相同的 分布,问任取一只灯泡,其寿命X 不低于1100小时的概率?
分析 寿命分布未知,P{X ≥1100}无法精确求得; 直观想法 测若干只灯泡的寿命,统计寿命不低于1100小时 的灯泡数量,求得频率f,用于近似概率P{X ≥1100}。
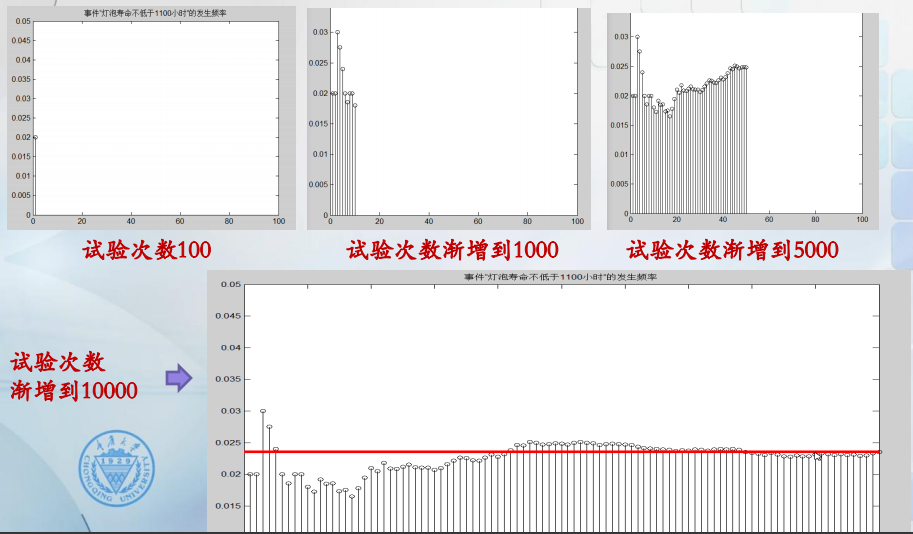
100次试验后,灯泡寿命不低于1100小时的发生概率为0.02...随着试验的次数增多,事件发生的频率趋向于时间发生的概率。
两个疑问 用“多次试验中事件发生的频率”去估计“一次试验事 件发生的概率”合理吗?
- ① 频率是否是稳定的?
- ② 频率是否是稳定到概率?
大数定律对这两个问题作出了肯定的回答,是频率稳定性的理论保证,大数定律是概率论中最著名的成果。
大数定律是有切比雪夫不等式推导而成,而切比雪夫不等式是由马尔科夫不等式推导而成。
马尔可夫不等式证明过程:
- 分段函数:x为非负函数,当0<x<a时,f(x)=0;当x>=a时,f(x)=a。
- 把x<a与x>=a分开证明,得出a×f(x) <= x
- 不等式两边去平均值(期望),最总得到P(x>=a) <= E(x)/a
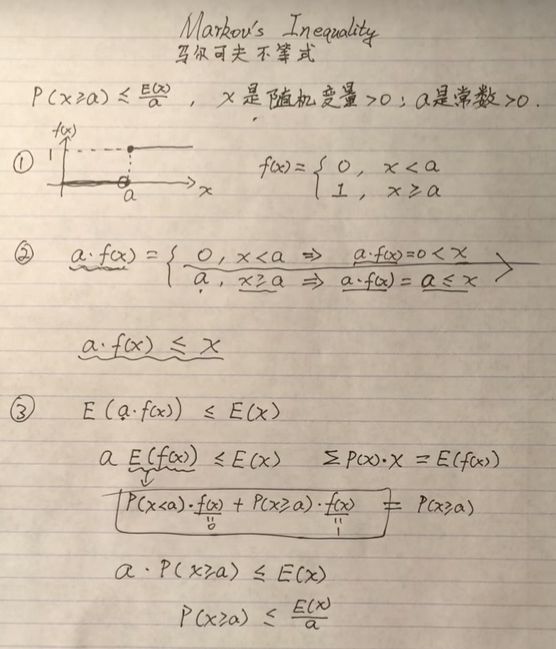

切比雪夫不等式: 利用方差来估计随机变量与它的数学期望的绝对偏差的一个概率估计数。其中x是随机数,μ是均值。x-μ的绝对值>=一个常数a的概率<=Var(x)/a2。
即若随机变量x的期望和方差都存在,x与μ的差
切比雪夫不等式证明过程:
- 若x是一个随机数,则x减去一个常数,同样得到也是一个随机数。
- 证明P(|x-μ|>=a) 等于 P((x-μ)2>=a2).
- {x>=a+μ or x<=-a+μ}的意思是x是落在阴影部分。即有50%的概率{|x-μ|>=a}是成立的,所以|x-μ|>=a的概率等于{x>=a+μ or x<=-a+μ}的概率。
- 同理,证明出(x-μ)2>=a2的概率等于{x>=a+μ or x<=-a+μ}的概率。
- 综上2点,的得到P(|x-μ|>=a) 等于 P((x-μ)2>=a2)
- 将X=x-μ代入马尔可夫不等式,得出P(|x-μ|>=a) <= Var(x)/a2,即切比雪夫不等式。




上图中,随机变量的取值位于u-epsilon的左侧或位于u+epsilon的右侧,这样事件的概率是有上界的,即为Sigma平方/Epsilon平方。 这样也说明了方差是刻画随机变量关于其均值波动的数字特征,方差越大,此概率的上界也就越大。

依概率收敛:
概率论是研究随机现象经过大量实验以后呈现出的统计规律性的一门学科,而研究大量的有力工具即为极限,所以再概率论中,要引入极限。


随机变量序列是指由随机变量构成的一个极限。在高度数学中,数列Xn的极限为C,它的定义方式:当n充分大时,Xn与C之间的距离任意的小,即|Xn-C|<Epsilon,n->无穷大。
而随机变量Xn的极限时C,当n充分大时,Xn与C的距离任意小。这是错的。


A的频率是随机变化的,当n的改变,我们得到一个随机序列,会与0.5非常接近。但n充分大时,两者距离任意小,是错误的。因为可能出现极端的情形,n次抛的结果为正面,两者的距离等于0.5。出现这种极端的情形的概率为1/2^n。当n趋向于无穷大时,它的概率收敛到0。通过证明我们可以得到,频率和0.5之间出现较大的偏差的可能性的极限为0。当n充分大时,两者任意接近的可能性为1。在概率的意义上就保证了极限为0.5,此时称依概率收敛到0.5.


随着n的增大,曲线越来越陡峭。Xn依概率趋向于0的概率趋向于1.

如果Xn依概率收敛于C,Yn依概率收敛于b,则随机变量序列的函数依概率收敛于其极限的函数。
大数定律:
三个大数定律:切比雪夫大数定律,独立同分布情形下的大数定律,贝努利大数定律。


切比雪夫大数定律:X_bar依概率收敛于E(X)=E(X_bar)。注:任意两个随机变量是不相关。


独立同分布情形下的大数定律是切比雪夫大数定律的特例,其中任意两个随机变量是独立的。


贝努利大数定律解释了概率的统计定理当中频率的稳定性。

贝努利大数定理还有用来解释小概率原理,即小概率事件在一次试验中是不发生的,因为频率依概率收敛的极限为其概率,既然其概率很小,那么它的频率也应很小。一次试验当中,事件的频率或为0或为1,既然很小,我们就应当认定其为0,也即它在一次试验当中是不发生的。
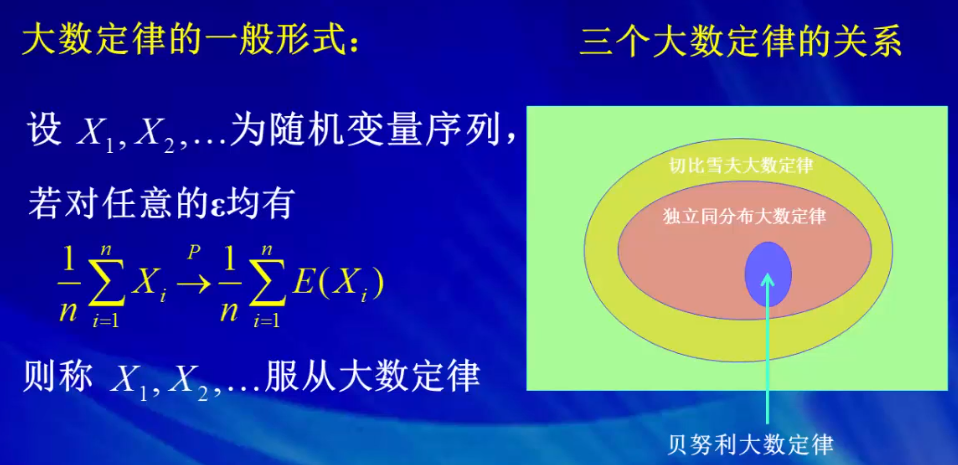
前n项的算术平均依概率收敛到前n项期望的算术平均,即这个随机变量序列服从大数定律。
三个大数定律的关系:
- 切比雪夫大数定律:它要求随机变量两两不相关,并且方差是有界的。
- 独立同分布的大数定律:它要求随机变量独立同分布,并且每个随机变量的期望和方差都存在。它是切比雪夫大数定律的特例。
- 贝努利大数定律:它不仅要求随机变量独立同分布,还要求每个变量都服从两点分布。它是独立同分布大数定律的特例。

回到引例
引例中,通过试验模拟,得到灯泡寿命不低于1100小 时的频率逐渐稳定在0.0235 左右,由强大数定律,结论“ 任取一只灯泡,其寿命不低于1100小时的概率P{X ≥1100}= 0.0235 ”是合理的,随着试验次数的增大,这个频率趋于真实概率的可能性趋于1。


一般形式: 在适当的条件下,对于任意的正整数k,前一项k次方的概率平均,依收敛Xi的k次方的期望。这就是统计学中,矩估计的原理。

2. 中心极限定理
引问:为什么世界上的大多数分布服从正太分布?
其内在原因就是随机现象背后中心极限定理的存在。


正态分布:

![]()
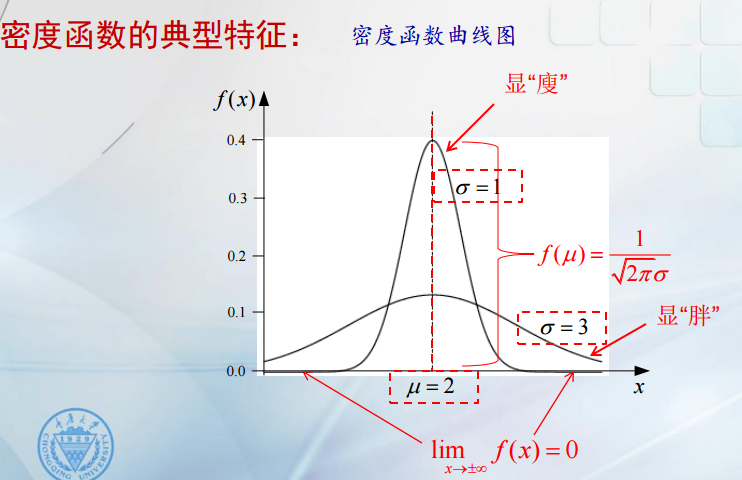
正太分布的密度函数的典型特征:
- μ是曲线的对称点,它决定曲线的中心位置,称为位置参数。
- 函数f(x)在μ处达到最大值。f(μ)=1/(2∏*σ)0.5
- 参数σ值越小,曲线显瘦,反之曲线显胖。称参数σ为形状参数。
- 当x趋于+-无穷时,limf(x)=0。
- 当μ=0,σ=1时,函数分布为标准正态分布。
多重随机变量独立且服从0-1分布,当n趋向于无穷大是,多重随机变量联合分布服从正态分布。

引例一 炮弹落点误差问题?
炮弹落点误差的因素有多个,如士兵瞄准误差,空气阻力误差等等。求多重随机变量的和分布:


所以Yn服从正态分布。

随机变量序列由随机变量X1..Xn,两两独立同分布构成, 随机变量之和的期望是nu,随机变量之和的方差,因为独立,它的方差等于方差之和为n*Signma平方。这里的极限公式中,将前项标准化后为Singma(1~n)Xi,它小于x,当n趋于无穷大时,极限恰为标准正太分布函数,称这个变量序列具有标准正太极限分布。

条件:
- 相互独立说明随机变量相互不影响,
- 同分布说明它们在和当中的地位时相同的,且作用时微小的。 并没有限定她们共同分布的类型,可以是离散,连续或其他类型。
结论:
- 当期望和方差都存在时,和经过标准化即有标准正太的极限分布。
- 哪怕分布不相同,只要随机变量在和当中的地位都是微小的,就有类似的结论(可近似服从正太分布)。
例如测量误差受到环境温度、湿度、测量工具精度和测量者心情的随机因素的影响,由于这些随机变量是相互独立的,所以测量误差受到的影响是微小的,且他们的和造成的总的测量误差近似服从正态分布。
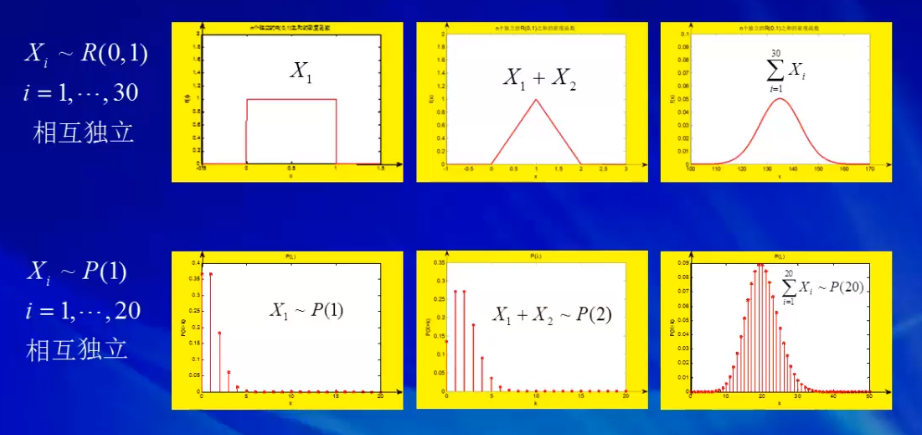
例如:1个到30个相互独立的均匀分布之和的密度函数图像,随着随机变量的个数的增加,它的分布越来越接近正太分布。
1个到20个相互独立的泊松分布之和的概率函数图像,随着随机变量的个数的增加,它的分布越来越接近正太分布。
中心极限定理推广
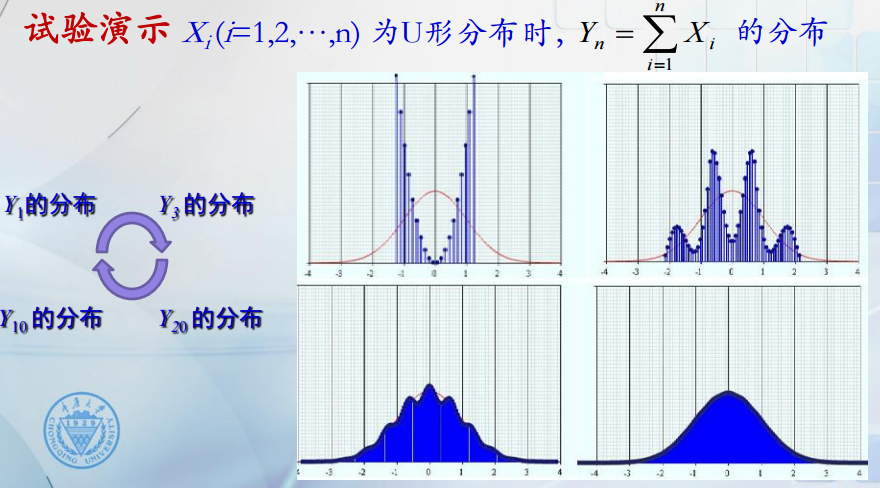
若X1 ,X2 ,…,Xn ,…独立同分布,但不是0-1分布时,Yn服从什么分布?
如图所示,随着随机变量的增多,联合分布会趋向于正态分布。




当n较大时,Xi的和经过标准化,近似服从标准分布。在标准化之前,Xi的和也是服从正太分布,其参数为nu和n*sigma平方。如果将Xi的和除以n,为Xi_bar,也是服从正太分布的,其参数为u,Sigma平方/n。



由于Xi的分布未知,所以Xi和的分布也是未知的。这里n较大,我们就可以利用极限分布作为近似分布进行计算。



德莫弗-拉普拉斯中心极限定理,又称为二项分布的正态近似。


当Y服从二项分布,P(a<Y<b)可以用二项公式表示,当n较大时,Y就近似服从正太分布,然而,当n小,p较小时,Y服从泊松分布。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号