S&P_01 概率空间和概率基本概念

概率论与数理统计公式整理

 

概率论与数理统计及Python实现：https://www.cnblogs.com/Belter/p/8330773.html

概率论

---

 

01. 概率论中的基本概念

02. 随机变量概述

03. 一维离散型随机变量及其Python实现

04. 一维连续性随机变量及其Python实现

05. 随机变量的数字特征

数理统计

---

 

06. 大数定律及中心极限定理

07. 统计学中的基本概念

08. 三大抽样分布

09. 参数估计：参数估计概述，点估计，区间估计

10. 参数假设检验

11. 拟合优度检验（非参数假设检验）

12 方差分析

13. 回归分析

 

01 概率论与数理统计：

    实际上，一般概率论与数理统计被认为是两个学科。

    概率论是数学的一个分支，研究如何定量描述随机变量及其规律；

    数理统计则是以数据为唯一研究对象，包括数据的收集、整理、分析和建模，从而对随机现象的某些规律进行预测或决策。

 

02  随机变量概述

随机变量与事件的联系与区别

对于随机试验，我们所关心的往往是与所研究的特定问题有关的某个或某些量，而这些量就是随机变量。当然，有时我们所关心的是某个或某些特定的随机事件。例如，在特定一群人中，年收入在万元以上的高收入者，以及年收入在3000元以下的低收入者，各自的比率如何？这看上去像是两个孤立的事件。可是，若我们引入一个随机变量XX： 

　　　　　　X=随机抽出一个人其年收入X=随机抽出一个人其年收入 

则X是我们关心的随机变量。上述两个事件可分别表示为{X>10000}或{X<3000}。这就看出：随机事件这个概念实际上包容在随机变量这个更广的概念之内。也可以说，随机事件是从静态的观点来研究随机现象，而随机变量则是一种动态的观点，一如数学分析中的常量与变量的区分那样，变量概念是高等数学有别于初等数学的基础概念。同样，概率论能从计算一些孤立事件的概率发展为一个更高的理论体系，其基本概念就是随机变量。

随机变量的基本性质

缩写	全拼	中文名	解释
CDF	Cumulative Distribution Function	累计分布函数	连续型和离散型随机变量都有，一般用F(X)表示
PDF	Probability Density Function	概率密度分布函数	连续型随机变量在各点的取值规律，用f(x)或fX(x)表示
PMF	Probability Mass Function	概率质量分布函数	离散随机变量在各特定取值上的概率
RVS	Random Variate Sample	随机变量的样本	从一个给定分布取样
PPF	Percentile Point Function	百分位数点函数	CDF的反函数
IQR	Inter Quartile Range	四分位数间距	25%分位数与75%分位数之差
SD	Standard Error	标准差	用于描述随机变量取值的集中程度
SEM	Standard Error of the Mean	样本均值的估计标准误差， 简称平均值标准误差
CI	Confidence Interval	置信区间

 

03. 一维离散型随机变量及其Python实现

1. 伯努利分布

每种分布都是一种模型，都有其适用的实例。伯努利分布适合于试验结果只有两种可能的单次试验。例如抛一次硬币，其结果只有正面或反面两种可能；一次产品质量检测，其结果只有合格或不合格两种可能。

伯努利分布只有一个参数p，记做X∼Bernoulli(p)，或X∼B(1,p)，读作X服从参数为p的伯努利分布。

2. 二项分布

如果把一个伯努利分布独立的重复n次，就得到了一个二项分布。二项分布有两个参数——试验次数n和每次试验成功的概率p. 其概率质量函数为：

　　　　

 

 

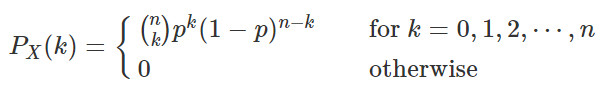
一个随机变量X服从参数为n和p的二项分布，记做X∼Binomial(n,p)，或X∼B(n,p) 。随机变量X要满足这个分布有两个重要条件：

• 各次试验的条件是稳定的；
• 各次试验之间是相互独立的。

现实生活中有许多现象程度不同地符合这些条件，例如经常用来举例子的抛硬币，掷骰子等。如果每次试验条件都相同，那么硬币正面朝上的次数以及某一个点数出现的次数都是非常典型的符合二项分布的随机变量。均匀硬币抛1000次，则正面朝上的次数X∼Binomial(1000,0.5)；有六个面的骰子，掷100次，则6点出现的次数X∼Binomial(100,16)

3. 泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。

泊松分布有一个参数λ（有的地方表示为μ），表示单位时间（或单位面积）内随机事件的平均发生次数，其PMF表示为：

　　　　

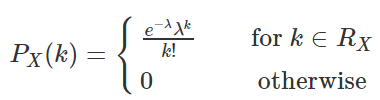
一个随机变量X服从参数为λ (或者mu) 的泊松分布，记做X∼Poisson(λ)，或X∼P(λ)。

4. 泊松分布与二项分布的关系

如果仅仅是看二项分布与泊松分布的概率质量分布图，也可以发现它们的相似度非常高。事实上这两个分布内在联系十分紧密。泊松分布可以作为二项分布的极限得到。一般来说，若X∼B(n,p)，其中n很大，p很小，而np=λ不太大时，则X的分布接近于泊松分布P(λ).

从下图中可以非常直观的看到两者的关系：

 

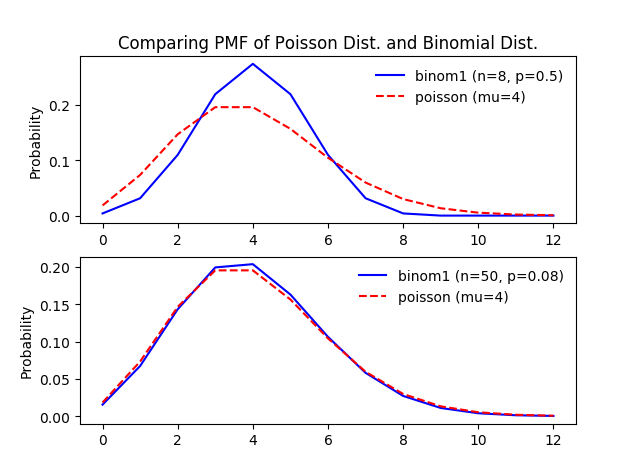
上面的图中二项分布的参数n比较小，p比较大，与参数为μ=np的泊松分布差异很大；下面的图中二项分布的参数n比较大，两者的PMF图已经非常相似了。

从取值范围上来说：

• 二项分布的取值范围内为[0,n]；
• 泊松分布的取值范围为[0,+∞]；

当二项分布的参数n→+∞时，在np不变的情况下，单位长度上发生的概率降低了。

 

04. 一维连续性随机变量及其Python实现

1. 均匀分布

如果连续型随机变量 X 具有如下的概率密度函数，则称 X 服从 [a,b] 上的均匀分布（uniform distribution）,记作X∼U(a,b) 或 X∼Unif(a,b)。

　　　　

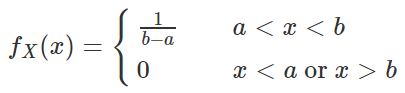
均匀分布具有等可能性，也就是说，服从 U(a,b) 上的均匀分布的随机变量 X 落入 (a,b) 中的任意子区间上的概率只与其区间长度有关，与区间所处的位置无关。

由于均匀分布的概率密度函数(PDF)是一个常数，因此其累积分布函数(CDF)是一条直线，即随着取值在定义域内的增加，累积分布函数值均匀增加。

　　　　　　　 

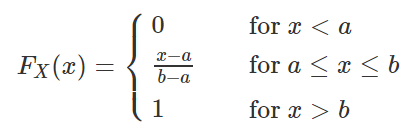
• 设通过某站的汽车10分钟一辆，则乘客候车时间 X 在 [0,10] 上服从均匀分布；
• 某电台每个20分钟发一个信号，我们随手打开收音机，等待时间 X 在 [0,20] 上服从均匀分布；
• 随机投一根针与坐标纸上，它和坐标轴的夹角 X 在  [0,π] 上服从均匀分布。

2. 指数分布

如果一个随机变量 X 的概率密度函数满足一下形式，就称 X 为服从参数 λ 的指数分布(Exponential Distribution)，记做 X∼E(λ)或 X∼Exp(λ).

指数分布只有一个参数 λ，且 λ>0.

　　　　

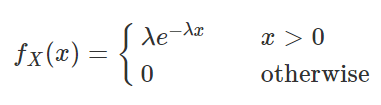
其实指数分布和离散型的泊松分布之间有很大的关系。泊松分布表示单位时间（或单位面积）内随机事件的平均发生次数，指数分布则可以用来表示独立随机事件发生的时间间隔。由于发生次数只能是自然数，所以泊松分布自然就是离散型的随机变量；而时间间隔则可以是任意的实数，因此其定义域是 (0,+∞)。

• 表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等；
• 在排队论中，一个顾客接受服务的时间长短也可以用指数分布来近似；
• 无记忆性的现象（连续时间）。

指数分布的一个显著的特点是其具有无记忆性。例如如果排队的顾客接受服务的时间长短服从指数分布，那么无论你已经排了多久时间的队，在排 t 分钟的概率始终是相同的。 

 

3. 指数分布与泊松分布的关系

先总体上比较一下这两个分布：

• 在泊松分布中，时间是固定的(例如单位时间内)，研究的随机变量 X 是某事件在该时间段内出现的次数。其均值为 λ，表示某随机事件在单位时间内平均发生的次数；
• 在指数分布中，出现的次数是固定的（比如出现了1次），研究的是随机变量T 出现（发生，或到达）1次需要的时间。其均值为 1/λ，表示某随机事件发生一次的平均时间间隔。
• λ越大，表示单位时间里发生的次数就越多，那么每两次事件之间的时间间隔1/λ也就越小。

已知泊松分布在时间tt上的PMF为（此时可以将tt看做是一个固定的常数）：

 　　　　

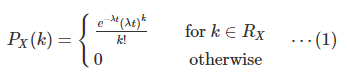
泊松过程中，第k次随机事件与第k+1次随机事件出现的时间间隔服从指数分布。而根据泊松过程的定义，我们定义 TT 为两次随机事件出现的时间间隔。此时 TT 是一个随机变量，并且可以得到 TT 的分布函数为：

 　　　　F(t)=Pr(T≤t)　　⋯(2)

 上式就等于，

　　　　F(t)=Pr(T≤t)=1−Pr(T>t)　　⋯(3)

 在长度为 t 的时间段内没有随机事件出现的概率，即时间间隔大于tt，（下面的式子是理解泊松分布与指数分布之间关系的关键！）：

 　　　　Pr(T>t)=Pr(随机事件在时间t内出现了0次)=Pr(X=0)=e−λt(λt)00!=e−λt　　⋯(4)

将上式带入 (3) 式就可以得到：

 　　　　F(t)=1−e−λt⋯(5) 

这个式子就是指数分布的累积分布函数，对 (5) 式求导后，就可以得到指数分布的概率密度函数，同定义中给出的形式。

 

举一个例子来更好的理解指数分布和泊松分布之间的关系：

这个例子来源于泊松分布的wiki主页，一条河平均100年会有一次洪水泛滥，那么如何来求时间小于某个时间点，会有洪水发生的概率？

根据题意可得，如果将100年作为一个单位时间，那么 λ=1λ=1，即在单位时间内平均发生洪水泛滥的次数。

那么根据 (5) 式就可以计算出小于某个特定时间点，可能会发生洪水的概率。

下面是分别取 λλ 为1, 0.2和5得到的指数分布的 CDF 图。

 图4-1, 取每一百年不同的洪水泛滥次数，得到的以洪水泛滥发生时间为随机变量的CDF图

上图可以理解为，如果每100年发生洪水的次数越多（λλ 越大），那么下一次发生洪水的时间间隔越短。例如我们取时间为2.5， 表示第250年，则会预期在250年内发生洪水泛滥的概率：

• 蓝色线的概率取值几乎为1 ，表示如果100年内平均会发生5次洪水的情况下，250年内几乎肯定会发生至少一次洪水泛滥；
• 绿色线的概率大概为0.4，表示如果100年内平均发生0.2次，也就是说基本上500年才发生一次，那么250年内发生的概率就会比较小，但也不是不可能。

4. 正态分布

若随机变量 X 的概率密度符合下面的形式，就称 X 服从参数为 μ,σ 的正态分布（或高斯分布），记为 X∼N(μ,σ2).

　　　　 

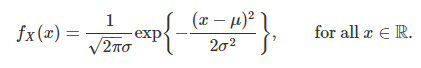
如果上面公式中 μ=0,σ=1，就叫做标准正态分布，一般记做 Z∼N(0,1)。

 正太分布的密度函数的典型特征：

• μ是曲线的对称点，它决定曲线的中心位置，称为位置参数。
• 函数f(x)在μ处达到最大值。f(μ)=1/(2∏*σ)^0.5
• 参数σ值越小，曲线显瘦，反之曲线显胖。称参数σ为形状参数。
• 当x趋于+-无穷时，limf(x)=0。
• 当μ=0，σ=1时，函数分布为标准正态分布。

正态分布中两个参数含义：

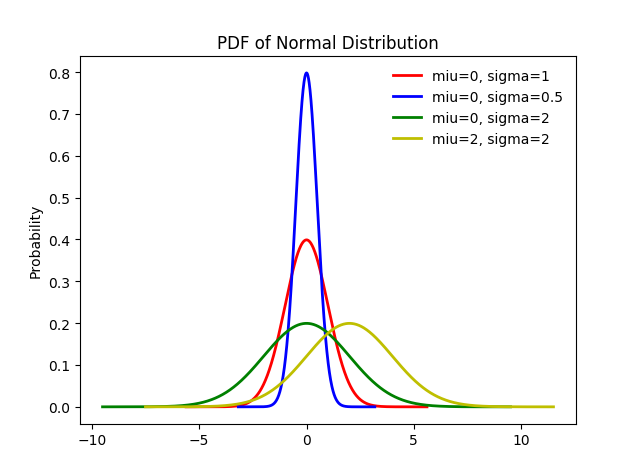
• 当固定 σ，改变 μ 的大小时，f(x) 图形的形状不变，只是沿着 x 轴作平移变换，因此 μ 被称为位置参数（决定对称轴的位置）；
• 当固定 μ，改变 σ 的大小时， f(x) 图形的对称轴不变，形状改变， σ 越小，图形越高越瘦， σ 越大，图形越矮越胖，因此 σ 被称为尺度参数（决定曲线的分散程度）

 

 05. 随机变量的数字特征

1. 数学期望（Mathematical Expectation）

一个随机变量XX的数学期望，简称期望，也叫作均值（Mean），记为E(X)。常见随机变量的定义中，都直接或间接包含了“期望”这个参数，该参数一般与分布在坐标轴上的位置有关。期望与我们平时说的平均值差不多，体现的是随机变量中的“大多数”的取值情况或趋势。

在计算时，随机变量X的平均值E(X)并不等同于一个具体样本集xx的均值E(x) —— 计算一个具体样本集的均值时，是将所有的值求和然后除以样本个数，因为此时的xx已经是一个具体的数列，而不再具有随机性 —— 随机变量X的均值是加权平均数。

例如，一个离散型随机变量XX的概率质量分布列如下：

图1-1, 概率质量分布函数

那么根据定义，E(X)=∑i=1nxipi=0×0.15+1×0.3+2×0.25+3×0.2+4×0.1=1.8；如果我们从该随机变量中取1个样本集x1=1,1,2,4,4x1=1,1,2,4,4，那么E(x1)=(1+1+2+4+4)/5=2.4

 

数学期望的性质：

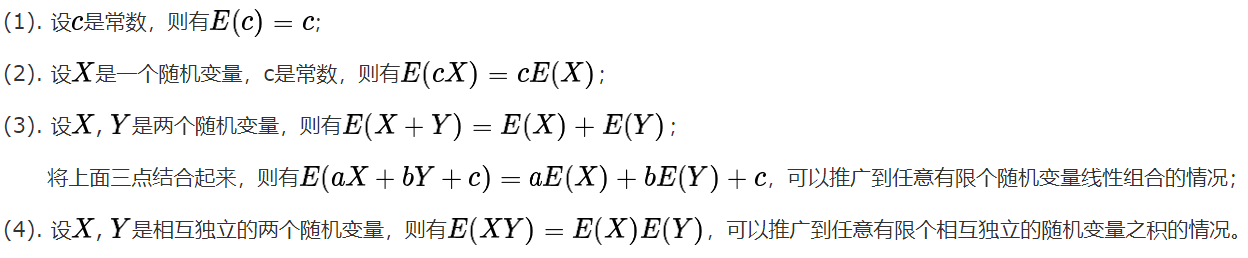
常见分布的期望:

•  0-1分布，X∼B(1,p)，则E(X)=p；
• 二项分布，X∼B(n,p)，则E(X)=np；
• 泊松分布，X∼P(λ)，则E(X)=λ；
• 几何分布，X∼G(p)，则E(X)=1/p；
• 均匀分布，X∼U[a,b]，则E(X)=(a+b)/2；
• 正态分布，X∼N(μ,σ2)，则E(X)=μ；
• 指数分布，X∼E(λ)，则E(X)=1/λ；

2. 方差（Variance）

一个随机变量X的方差，刻画了X取值的波动性，是衡量该随机变量取值分散程度的数字特征。方差越大，就表示该随机变量越分散；方差越小，就表示该随机变量越集中。在实际应用中，例如常见的关于“射击”的例子中，如果一个运动员打靶得分的方差大，就表示该运动员打在靶上的位置比较分散，成绩不稳定；相反则表示打在靶上的位置比较集中，成绩稳定。

常见分布的方差

•  0-1分布，X∼B(1,p)，则D(X)=p(1−p)；
• 二项分布，X∼B(n,p)，则D(X)=np(1−p)；
• 泊松分布，X∼P(λ)，则D(X)=λ,(λ>0)，与E(X)相同；
• 几何分布，X∼G(p)，则D(X)=(1−p)/p2；
• 均匀分布，X∼U[a,b]，则D(X)=(b−a)2/12；
• 正态分布，X∼N(μ,σ2)，则D(X)=σ2,(σ>0)；
• 指数分布，X∼E(λ)，则E(X)=1/λ2,(λ>0)，E(X)的平方；

期望，方差，数学期望，样本均值，样本方差之间的区别

• 样本均值：我们有n个样本，每个样本的观测值为Xi，那么样本均值指的是 1/n * ∑x(i)，求n个观测值的平均值
• 数学期望：就是样本均值，是随机变量，即样本数其实并不是确定的

 　　　　PS：从概率论的角度而言：样本指的是我们现在有多少东西需要去观测，它是一种随机变量，即样本的多少是不确定的，我们得到的样本均值并不是真正意义上的期望。

• 期望：已知其观测值f（x）及其概率P，求其观测值与概率乘积的累加和，∑Xi*Pi

　　　　  

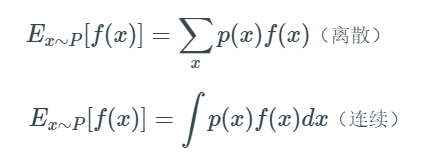
　　　　PS：期望是一种固定值，他的观测值是基于已知某几类数值及其概率，是不同于数学期望中的观测值Xi的，数学期望         的观测值有一点取决于样本数量的味道，也就是求和这里的n其实是不同的

• 方差：

　　　　

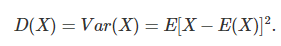
• 样本方差的计算：样本方差一般用S²表示。按照方差的定义：

　　　　

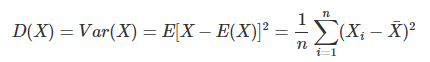
　　　　其中X¯=E(X)。如果直接用上面的公式计算S²，等同于使用样本的二阶中心距（矩的概念在下面介绍）。但是样本的二阶中心距并不是随机变量X这个总体分布的无偏估计，将上式中的n换成n−1就得到了样本方差的计算公式，这也是总体方差的无偏估计。

 　　　　

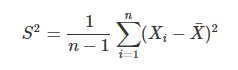
　　　　从直观上来理解，由于样本方差中多了一个约束条件 —— 样本的均值是固定的，E(X)=X¯ —— 如果已知 n−1 样本，那么根据均值可以直接计算出第 n个样本的值，因此自由度比计算总体方差的时候减小了1个。 

　　　　这里的观测值减去的是均值！均值的意思就是原本物质所存在的均值，即 1/n * ∑x(i)，而实际上我们可以得知方差的求解应该减去的是期望E(X) 才对，其中的缘故在于我们并不能得知真正的期望是多少，只能通过随机变量的样本求得一个近似的值来预估期望，即利用下式来证明： ， 当theta值是样本均值的时候，该式值最小（每个值减他们总和的均值），那么同理返回样本方差的等式，上式最小意味着利用样本均值求解样本方差会把真实方差算小了，因此将N处理成N-1来增大样本方差的值引出两个结论：

　　（a）当分母为N-1的时候，是我们对方差做的一个无偏估计

　　（b）当分母为N的时候，是我们对方差做的一个极大似然估计
总结：　　

• 样本均值是数学期望，求的是n个观测值的平均值，而期望指的是观测值及其概率的乘积的累加和
• 在样本足够多的情况下，可以理解为样本均值趋近于期望E 即：1/n*∑x(i) ≈ ∑p(i)*x(i) 
• 方差的本质是固定不变的，得到的是这个状态正儿八经与期望的偏差，
• 而样本方差是随机变量，得到的是也是一种偏差，只不过这种偏差是对正确偏差的一种估计值。

 

3. 矩

定义：若E(X^k),k=1,2,...存在，则称E(X^k)为X的k阶原点矩，记为α^k=E(X^k)

           若E[X−E(X)]^k,k=1,2,.....存在，则称E[X−E(X)]^k为X的k阶中心距，记为β^k=E[X−E(X)]^k

根据定义，期望E(X)是1阶原点矩，方差D(X)是2阶中心距。需要注意的是，就像上面提到过的，样本的2阶中心矩并不是总体方差的无偏估计，样本方差S²的实际计算公式中分母为n−1，而不是样本2阶中心距中的n。

4. 协方差和相关系数

4.1 协方差

协方差的计算公式可以化简为：Cov(X,Y)=E(XY)−E(X)E(Y)

4.2 相关系数

 　　

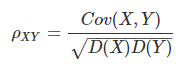
5. 样本均值的期望和方差 https://www.cnblogs.com/Belter/p/7629105.html

概率统计与机器学习：期望，方差，数学期望，样本均值，样本方差之间的区别：

https://www.cnblogs.com/tlfox2006/p/9456130.html

 

06. 大数定律及中心极限定理

1. 大数定律：随着试验次数的增大，这个频率趋于真实概率的可能性趋于1。大数定律讲的是，样本容量极大时，样本的均值必然趋近于总体的期望。

举例：用random模块生成区间[0,1)之间的随机数，如果生成的数小于0.5，就记为硬币正面朝上，否则记为硬币反面朝上。由于random.random()生成的数可以看做是服从区间[0,1)上的均匀分布，所以以0.5为界限，随机生成的数中大于0.5或小于0.5的概率应该是相同的(相当于硬币是均匀的)。这样就用随机数模拟出了实际的抛硬币试验。理论上试验次数越多(即抛硬币的次数越多)，正反面出现的次数之比越接近于1(也就是说正反面各占一半).

 

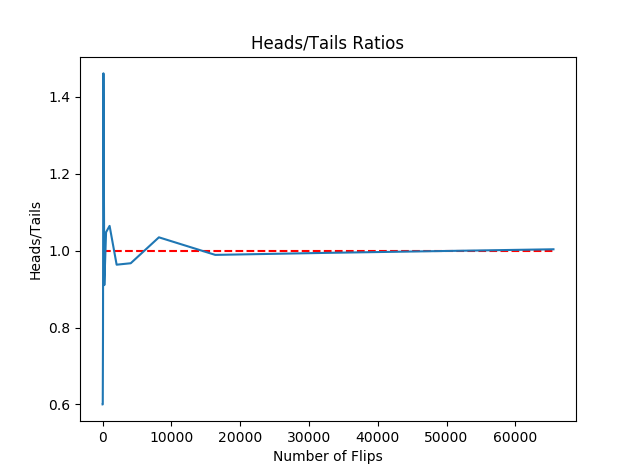
图，随着实验次数的增加，正反面出现次数之比越来越接近于1

2. 中心定理：多重随机变量独立且服从0-1分布，当n趋向于无穷大是，多重随机变量联合分布服从正态分布。中心极限定理讲的是：样本容量极大时，样本均值的抽样分布趋近于正太分布。这和样本所属的总体的分布的类型无关，样本所属总体的分布可以是正态分布，也可以不是。

3. 中心定理推广：多重随机变量独立同分布，当n趋向于无穷大是，多重随机变量联合分布服从正态分布。

简单来说，大数定律（LLN）和中心极限定理（CLT）的联系与区别在于：

• 共同点：都是用来描述独立同分布（i.i.d）的随机变量的和的渐进表现（asymptotic behavior)
• 区别：首先，它们描述的是在不同的收敛速率（convergence rate）之下的表现，其次LLN前提条件弱一点：E(|X|)<∞E(|X|)<∞ , CLT成立条件强一点：E(X2)<∞

 

07. 统计学中的基本概念 

0. 概率论与数理统计的异同

概率论、数理统计都是研究随机现象的统计规律性的数学分支，但两者研究角度不同。

概率论：从已知分布出发，研究随机变量X的性质、规律、数学特征等；

数理统计：研究对象X的分布未知或只知道部分信息，需要观察它的取值（数据采集），通过分析数据来推断X服从什么分布或确定未知参数。

1. 样本与总体

https://www.cnblogs.com/Belter/p/8029712.html

2. 统计量

统计量的概念存在于样本中，是对样本某个指标的概括，例如上面例子中选出来的100位学生的平均身高就是一个统计量。统计量区别于"个体量"（我自己生造的词），具有以下两个特点：

• 不包含任何未知数；
• 包含所有样本的信息。

因此只要样本确定，统计量的值就可以直接计算出来。例如一旦选定100位学生，他们的平均身高就可以计算出来。

2.1 常用统计量

 

 

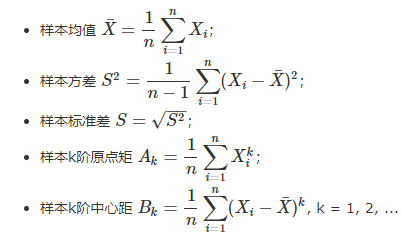
 2.2 从上面可以看到：样本的均值等于样本的1阶原点矩；但是样本的方差不等于样本的2阶中心距（在总体中这两者是相等的）；

用统计量估计总体的数字特征

当总体数字特征未知时，

• 用样本均值X¯估计总体均值μ=E(X)；
• 用样本方差S²估计总体方差σ²=E(X−μ)²；
• 用样本原点矩A_k估计总体原点矩α_k=E(X^k)；
• 用样本中心距B_k估计总体中心距β_k=E(X−μ)^k。

以上估计的理论基础就是大数定律。值得注意的是，总体的均值μ是一个数，可能已知，也可能未知；而样本均值X¯X¯是一个随机变量，依赖于样本值。

3. 抽样分布

统计量的分布被称为抽样分布。

当总体XX服从一般分布（如指数分布、均匀分布等），要得出统计量的分布是很困难的；当总体XX服从正态分布时，统计量X¯X¯、S2S2是可以计算的，且服从一定的分布。这些分布就是下面要介绍的三大抽样分布——χ2χ2分布，tt分布，FF分布。

 

 

 

 

 

https://wenku.baidu.com/view/11d3577e5acfa1c7aa00cc9b.html

排列与元素的顺序有关，组合与顺序无关．如231与213是两个排列，2＋3＋1的和与2＋1＋3的和是一个组合．

(一)两个基本原理是排列和组合的基础

(1)加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N＝m1＋m2＋m3＋…＋mn种不同方法．

(2)乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N＝m1×m2×m3×…×mn种不同的方法．

这里要注意区分两个原理，要做一件事，完成它若是有n类办法，是分类问题，第一类中的方法都是独立的，因此用加法原理；做一件事，需要分n个步骤，步与步之间是连续的，只有将分成的若干个互相联系的步骤，依次相继完成，这件事才算完成，因此用乘法原理．

这样完成一件事的分“类”和“步”是有本质区别的，因此也将两个原理区分开来．

(二)排列和排列数

(1)排列：从n个不同元素中，任取m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列．

从排列的意义可知，如果两个排列相同，不仅这两个排列的元素必须完全相同，而且排列的顺序必须完全相同，这就告诉了我们如何判断两个排列是否相同的方法．

(2)排列数公式：从n个不同元素中取出m(m≤n)个元素的所有排列

当m＝n时，为全排列Pnn=n(n－1)(n－1)…3·2·1＝n！

(三)组合和组合数

(1)组合：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从 n个不同元素中取出m个元素的一个组合．

从组合的定义知，如果两个组合中的元素完全相同，不管元素的顺序如何，都是相同的组合；只有当两个组合中的元素不完全相同时，才是不同的组合．

(2)组合数：从n个不同元素中取出m(m≤n)个元素的所有组合的个

这里要注意排列和组合的区别和联系，从n个不同元素中，任取m(m≤n)个元素，“按照一定的顺序排成一列”与“不管怎样的顺序并成一组”这是有本质区别的．

 

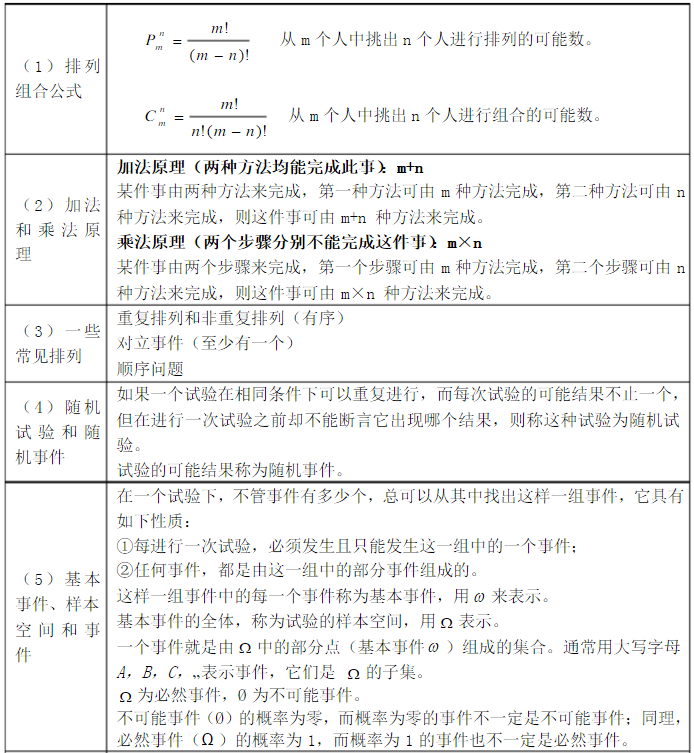
1. 随机试验与随机事件

如果一个实验事先能够明确地知道试验所有可能的基本结果，在每一次观察中，不能事先准确地预言其中哪一个基本结果会发生，并且在相同条件下可以重复进行，则称此试验为随机试验。

随机试验的每种基本结果称为一个样本点ω，全体基本结果构成的集合称为样本空间。

 

 

 2. 古典概型

 

 

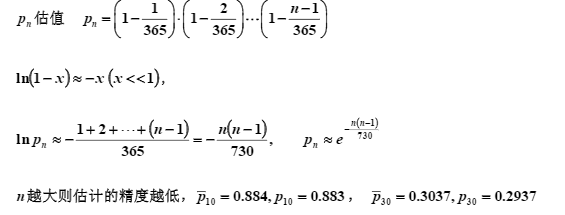
第一种，那个球是可分辨的，所以n个球做排列=》Pnn = n! 。而样本空间则为N^n，是因为每个球都有N个摆放的方式，属于乘法原理。

第二种，球是不可分辨的，所以n个球要做组合。 且每个盒子只能容纳一个球，所以样本空间为N!。

 

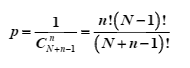
由于球是不可分辨的，4、5项可视为同一事件。 6、7项也可视为同一事件。8、9项也可视为同一事件。

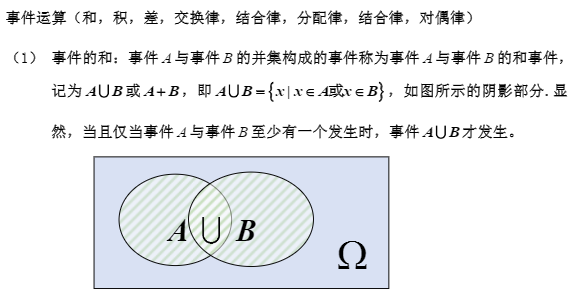
 1.3 事件间的关系与事件的运算

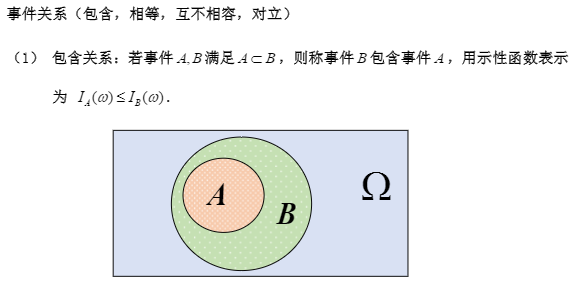
A包含于（）B，等于B包含事件A。