Python_Statistics&Probability

python_statistics and probability

https://blog.csdn.net/howhigh/article/details/78007317

https://www.jb51.net/article/152713.htm

常见分布

https://www.jianshu.com/p/c675e3f67843

Python 统计学

https://zhuanlan.zhihu.com/c_178173216

python实现

https://blog.csdn.net/charie411/article/details/100032776

1. 常用的统计分布

用Python统计模拟的方法，介绍四种常用的统计分布，包括离散分布：二项分布和泊松分布，以及连续分布：指数分布和正态分布，最后查看人群的身高和体重数据所符合的分布。
首先导入python相关模块：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

随机数
计算机发明后，便产生了一种全新的解决问题的方式：使用计算机对现实世界进行统计模拟。该方法又称为“蒙特卡洛方法（Monte Carlo method）”，起源于二战时美国研制原子弹的曼哈顿计划，它的发明人中就有大名鼎鼎的冯·诺依曼。蒙特卡洛方法的名字来源也颇为有趣，相传另一位发明者乌拉姆的叔叔经常在摩洛哥的蒙特卡洛赌场输钱，赌博是一场概率的游戏，故而以概率为基础的统计模拟方法就以这一赌城命名了。
使用统计模拟，首先要产生随机数，在Python中，numpy.random 模块提供了丰富的随机数生成函数。比如生成0到1之间的任意随机数：

np.random.random(size=5)  # size表示生成随机数的个数

结果：

array([0.12291039, 0.90953163, 0.19120842, 0.14675931, 0.94498984])

又比如生成一定范围内的随机整数：

np.random.randint(1, 10, size=5)  # 生成5个1到9之间的随机整数

结果：

array([2, 8, 6, 4, 2])

产生常见分布的随机数：

1）二项式或贝努力分布：

#np.random
np.random.binomial(10,0.5,size = 1000)

#scripy.stats
stats.binom.rvs(10,0.5,1000)

2) 指数分布

# np.random
np.random.exponential(10,size=1000)

# scipy.stats
stats.expon.rvs(10,size=1000)

3) 均匀分布

# np.random
np.random.uniform(-1,1,size=1000)

# scipy.ststs
stats.uniform.rvs(-1,1,size=1000)

4）正态分布

# np.random
np.random.normal(0,1,size=1000)

# scipy.stats
stats.uniform.rvs(-1,1,size=1000)

PMF&PDF

1）二项式分布

_lambda = 10.0             　　　　　　　　　　　　　# lambda恒等于10，二项分布的试验次数计算每次事件出现的概率p=lambda/n
k=np.arange(21)            　　　　　　　　　　　　　# 正面朝上次数
binom_100 = st.binom.pmf(k,100,_lambda/100)      # st.binom.pmf(k,n,p)
plt.plot(k,binom_100)

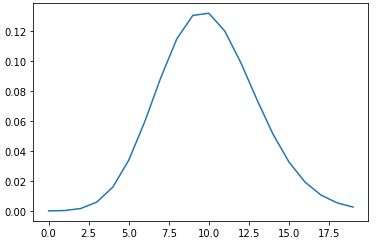
# np.binomial
binom_np = np.random.binomial(10,0.5,size=1000)

# plot PMF histogram
plt.hist(binom_np,bins=50)
hist_np = np.histogram(binom_np)[0]
plt.plot(hist_np)

# plot CDF
cdf_np = np.cumsum(hist_np)
plt.plot(cdf_np)

# st.binom
binom_st = st.binom.rvs(10,0.5,size=1000)

# plot histogram
plt.hist(binom_st,bins=50)
hist_st = np.histogram(binom_st)[0]
plt.plot(hist_st)

# plot CDF
cdf_st = np.cumsum(hist_st)
plt.plot(cdf_st)

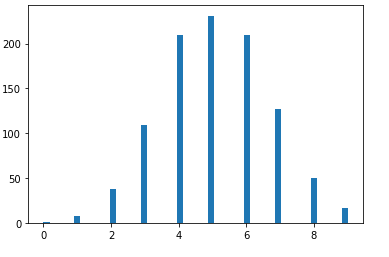
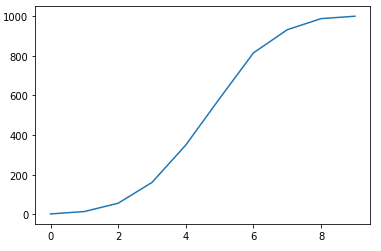
2）泊松分布

#泊松分布：在某段时间范围内，事件发生的次数。
_lambda = 10.0                # 事件平均发生率lambda恒等于10 
k = np.arange(20)             # 事件发生的次数。
psn = st.poisson.pmf(k,_lambda)    # st.poisson.pmf(k,Lambda)
plt.plot(k,psn)

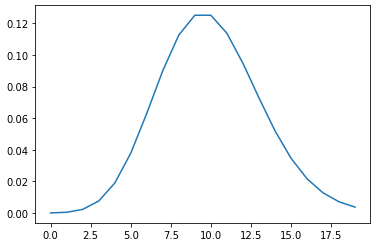
泊松分布与二项分布的关系：当n很大，而p很小时，二项分布可以近似于泊松分布。

3）均匀分布

4）指数分布

5）正态分布

下面介绍使用python生成pdf的方法：

使用matplotlib的画图接口plot.hist()，直接画出pdf分布；
使用numpy的数据处理函数histogram()，可以生成pdf分布数据，方便进行后续的数据处理，比如进一步生成cdf；
使用seaborn的distplot()，好处是可以进行pdf分布的拟合，查看自己数据的分布类型；Plot PDF

arr = np.random.normal(size=100)

# plot histogram
plt.subplot(221)
plt.hist(arr)

# obtain histogram data
plt.subplot(222)
hist, bin_edges = np.histogram(arr)
plt.plot(hist)

# fit histogram curve
plt.subplot(223)
sns.distplot(arr, kde=False, fit=stats.gamma, rug=True)
plt.show()

Plot PDF

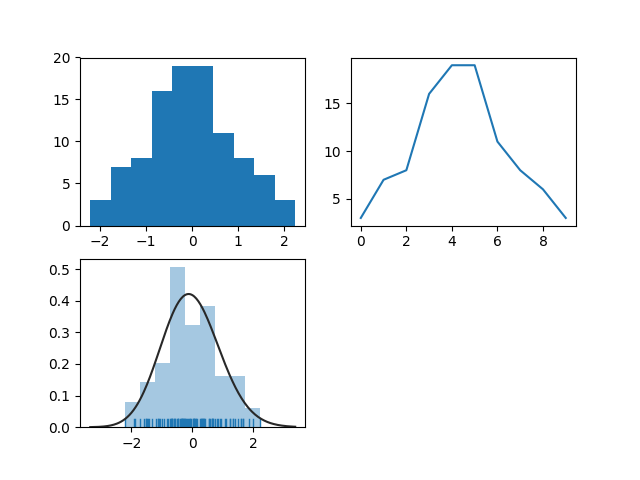
下面介绍使用python生成cdf的方法：

使用numpy的数据处理函数histogram()，生成pdf分布数据，进一步生成cdf；
使用seaborn的cumfreq()，直接画出cdf；

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

arr = np.random.normal(size=100)

plt.subplot(121)
hist, bin_edges = np.histogram(arr)
cdf = np.cumsum(hist)
plt.plot(cdf)

plt.subplot(122)
cdf = stats.cumfreq(arr)
plt.plot(cdf[0])

plt.show()

Plot CDF

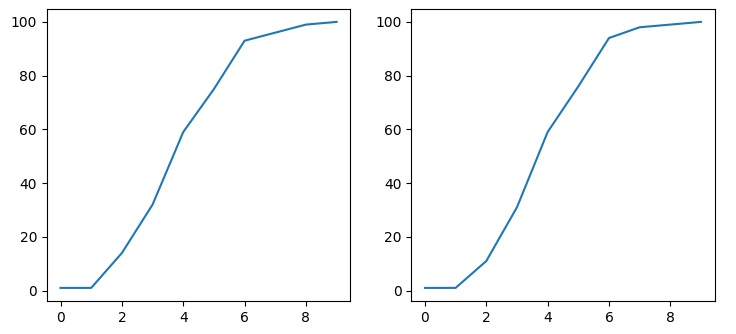
在更多时候，需要把pdf和cdf放在一起，可以更好的显示数据分布。

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

arr = np.random.normal(size=100)

hist, bin_edges = np.histogram(arr)
width = (bin_edges[1] - bin_edges[0]) * 0.8
plt.bar(bin_edges[1:], hist/max(hist), width=width, color='#5B9BD5')

cdf = np.cumsum(hist/sum(hist))
plt.plot(bin_edges[1:], cdf, '-*', color='#ED7D31')

plt.xlim([-2, 2])
plt.ylim([0, 1])
plt.grid()

plt.show()

CDF&PDF Consolidation

1) 二项分布

二项分布（伯努利分布）是n个独立的是/非试验中成功的次数的概率分布，其中每次试验的成功概率为p。这是一个离散分布，所以使用概率质量函数（PMF）来表示k次成功的概率：

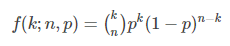
最常见的二项分布就是投硬币问题了，每次投一个硬币，投n次硬币，正面朝上次数就满足该分布。size（投掷次数）可以从10~10000. 看图形的变化。

sample=np.random.binomial(1,0.5,size=100)
plt.hist(sample,bins=50)

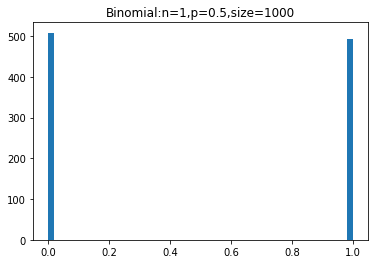
下面我们使用计算机模　　拟的方法，产生10000个符合（n，p）的二项分布随机数，相当于进行10000次实验，每次实验投掷了n（10）枚硬币，正面朝上的硬币数就是所产生的随机数。同时使用直方图函数绘制出二项分布的PMF图。

def plot_binomial_PDF(n,p,size):
    '''绘制二项分布的概率质量函数'''
    sample = np.random.binomial(n,p,size)  # 产生10000个符合二项分布的随机数
    bins = np.arange(n+2) 
    plt.hist(sample, bins=bins, align='left', normed=True, rwidth=0.1)  # 绘制直方图
    #设置标题和坐标
    plt.title('Binomial PMF with n={}, p={}'.format(n,p))  
    plt.xlabel('number of successes')
    plt.ylabel('probability')
def plot_binomial_CDF(n,p,size):
    sample=np.random.binomial(n,p,size)
    hist,bin_edges=np.histogram(sample)
    cdf=np.cumsum(hist/sum(hist))        #必须除以sum(hist)，才可以归一化。
    plt.plot(cdf)
plot_binomial_PDF(10, 0.5, 10000)
plot_binomial_CDF(10, 0.5, 10000)

Binomial PDF&CDF

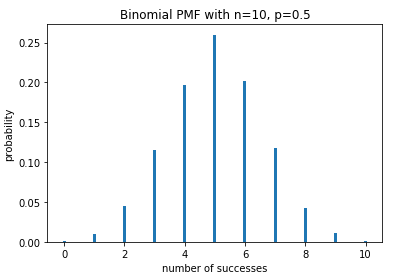
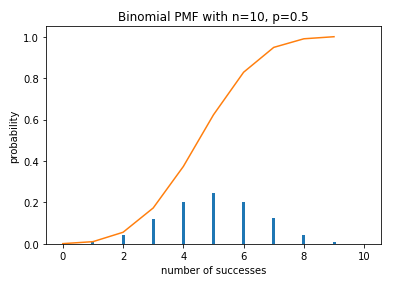
投10枚硬币，如果正面或反面朝上的概率相同，即p=0.5，那么出现正面次数的分布符合上图所示的二项分布。该分布左右对称，最有可能的情况是正面出现5次。
但如果这是一枚作假的硬币呢？比如正面朝上的概率p=0.2，或者是p=0.8，又会怎样呢？我们依然可以做出该情况下的PMF图。

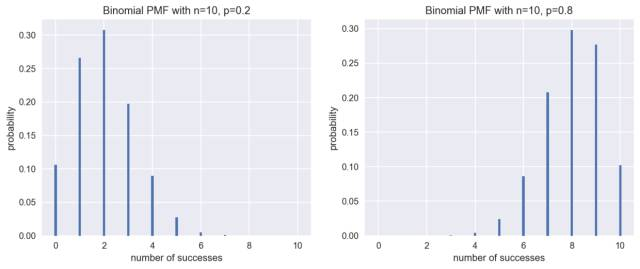
这时的分布不再对称了，正如我们所料，当概率p=0.2时，正面最有可能出现2次；而当p=0.8时，正面最有可能出现8次。

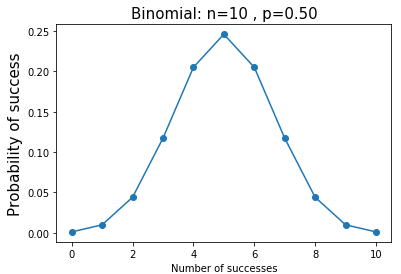
二项分布的例子：抛掷10次硬币，恰好两次正面朝上的概率是多少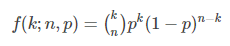？ --> k=2, n = 10, p=0.5

def binom_pmf():
     n = 10　　　　　　　　　　 #独立实验次数
     p = 0.5　　　　　　　　   #每次正面朝上概率
     k = np.arange(0,11)　　 #0-10次正面朝上概率
     binomial = stats.binom.pmf(k,n,p)
     print(binomial)
     print(sum(binomial))
     print(binomial[2])
     plt.plot(k, binomial,'o-')
     plt.title('Binomial: n=%i , p=%.2f' % (n,p),fontsize=15)
     plt.xlabel('Number of successes')
     plt.ylabel('Probability of success',fontsize=15)
     plt.show()

binomial PMF

[0.00097656 0.00976563 0.04394531 0.1171875  0.20507813 0.24609375
 0.20507813 0.1171875  0.04394531 0.00976563 0.00097656]
1.0000000000000009
0.04394531249999999

Output

2）泊松分布

泊松分布用于描述单位时间内随机事件发生次数的概率分布，它也是离散分布，其概率质量函数PMF为：

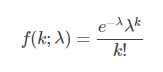
比如你在等公交车，假设这些公交车的到来是独立且随机的（当然这不是现实），前后车之间没有关系，那么在1小时中到来的公交车数量就符合泊松分布。同样使用统计模拟的方法绘制该泊松分布，这里假设每小时平均来6辆车（即上述公式中lambda=6）。

lamb = 6
sample = np.random.poisson(lamb, size=10000)  # 生成10000个符合泊松分布的随机数
bins = np.arange(20)
plt.hist(sample, bins=bins, align='left', rwidth=0.1, normed=True) # 绘制直方图# 设置标题和坐标轴
plt.title('Poisson PMF (lambda=6)')
plt.xlabel('number of arrivals')
plt.ylabel('probability')
plt.show()

Poisson PMF

根据图示，你会发现，泊松分布像正态分布，且λ=6的数据比较多。

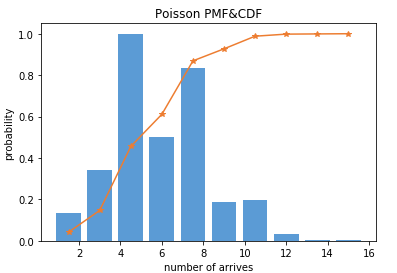
from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

arr = np.random.POISSON(5,size=100)

hist, bin_edges = np.histogram(arr)
width = (bin_edges[1] - bin_edges[0]) * 0.8
plt.bar(bin_edges[1:], hist/max(hist), width=width, color='#5B9BD5')

cdf = np.cumsum(hist/sum(hist))
plt.plot(bin_edges[1:], cdf, '-*', color='#ED7D31')

plt.title("Poisson PMF&CDF")
plt.xlabel("number of arrives")
plt.ylabel("probability")

Poisson PMF&CDF

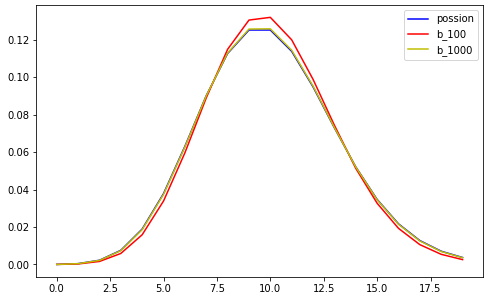
二项分布的近似分布泊松分布

程序分别计算二项分布和泊松分布的概率质量函数，当n足够大时，二者是十分接近的。
程序中事件平均发生率lambda恒等于10。根据二项分布的试验次数计算每次事件出现的概率p=lambda/n。lambda = np

_lambda = 10.0 
k = np.arange(20)
possion = stats .poisson .pmf(k, _lambda) # 泊松分布 
binom100 = stats.binom.pmf(k, 100, _lambda/100) #二项式分布 100
binom1000=stats.binom.pmf(k, 1000 , _lambda/1000) #二项式分布 1000

plt.figure(num=3,figsize=(8,5))
plt.plot(stats .poisson .pmf(k, _lambda),'b')
plt.plot(stats.binom.pmf(k,100,_lambda/100),'r')
plt.plot(stats.binom.pmf(k,1000,_lambda/1000),'y')
plt.legend(['possion','binom_100','binom_1000'])

Binomial & Possionb

3）均匀分布

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np

arr = np.random.uniform(-2,2,1000)

hist, bin_edges = np.histogram(arr)
width = (bin_edges[1] - bin_edges[0]) * 0.8
plt.bar(bin_edges[1:], hist/max(hist), width=width, color='#5B9BD5')

cdf = np.cumsum(hist/sum(hist))
plt.plot(bin_edges[1:], cdf, '-*', color='#ED7D31')
plt.title("Uniform PMF&CDF")
plt.xlabel("number of arrives")
plt.ylabel("probability")

plt.xlim([-2,2])
plt.ylim([0,1])

Uniform PDF&CDF

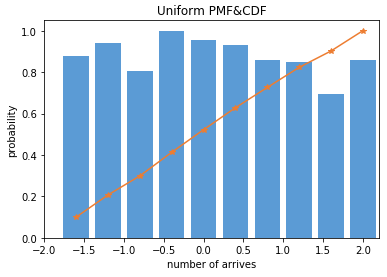
4) 指数分布

指数分布用以描述独立随机事件发生的时间间隔，这是一个连续分布，所以用质量密度函数表示：

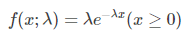
比如上面等公交车的例子，两辆车到来的时间间隔，就符合指数分布。假设平均间隔为10分钟（即1/lambda=10)，那么从上次发车开始，你等车的时间就满足下图所示的指数分布。

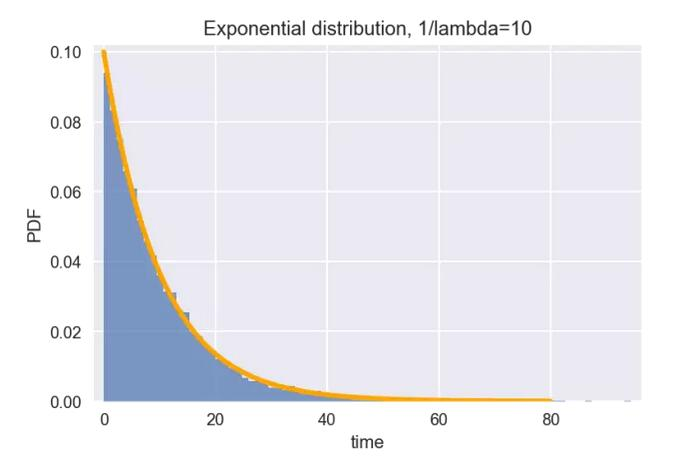
tau = 10
sample = np.random.exponential(tau, size=10000)  # 产生10000个满足指数分布的随机数
plt.hist(sample, bins=80, alpha=0.7, normed=True) #绘制直方图
plt.margins(0.02) 

# 根据公式绘制指数分布的概率密度函数
lam = 1 / tau
x = np.arange(0,80,0.1)
y = lam * np.exp(- lam * x)
plt.plot(x,y,color='orange', lw=3)#设置标题和坐标轴
plt.title('Exponential distribution, 1/lambda=10')
plt.xlabel('time')
plt.ylabel('PDF')
plt.show()

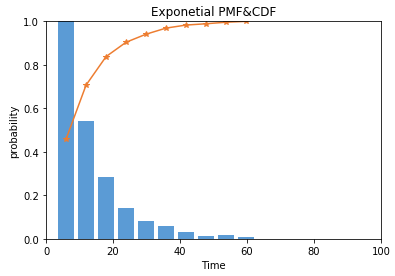
Exponential PDF&CDF:

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np

arr = np.random.exponential(10,1000)

#PDF
hist, bin_edges = np.histogram(arr)
width = (bin_edges[1] - bin_edges[0]) * 0.8
plt.bar(bin_edges[1:], hist/max(hist), width=width, color='#5B9BD5')

#CDF
cdf = np.cumsum(hist/sum(hist))
plt.plot(bin_edges[1:], cdf, '-*', color='#ED7D31')

plt.title("Exponetial PMF&CDF")
plt.xlabel("Time")
plt.ylabel("probability")
plt.xlim([0,100])
plt.ylim([0,1])

Exponential PDF&CDF

5) 正态分布

正态分布是一种很常用的统计分布，可以描述现实世界的诸多事物，具备非常漂亮的性质，其概率密度函数为

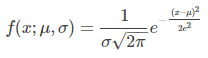
以下绘制了均值为0，标准差为1的正态分布的概率密度曲线，其形状好似一口倒扣的钟，因此也称钟形曲线

def norm_pdf(x,mu,sigma):
    '''正态分布概率密度函数'''
    pdf = np.exp(-((x - mu)**2) / (2* sigma**2)) / (sigma * np.sqrt(2*np.pi))    return pdf

mu = 0    # 均值为0
sigma = 1 # 标准差为1
# 用统计模拟绘制正态分布的直方图
sample = np.random.normal(mu, sigma, size=10000)
plt. hist(sample, bins=100, alpha=0.7, normed=True)# 根据正态分布的公式绘制PDF曲线
x = np.arange(-5, 5, 0.01)
y = norm_pdf(x, mu, sigma)
plt.plot(x,y, color='orange', lw=3)
plt.show()

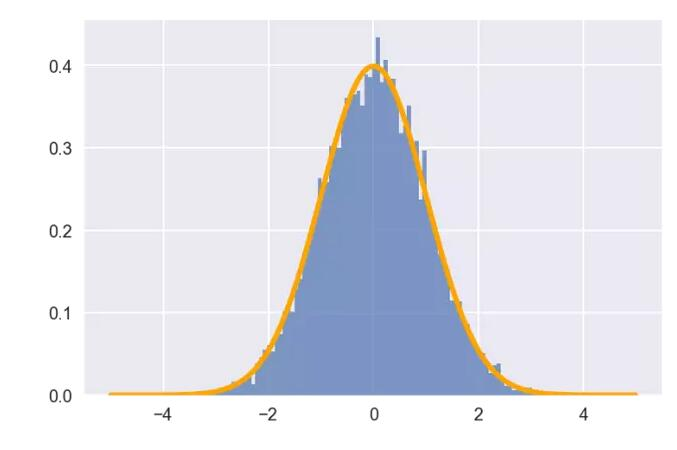
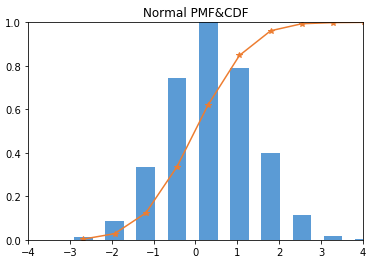
Normal PDF&CDF

from scipy import stats
import matplotlib.pyplot as plt
import numpy as np

arr = np.random.normal(0,1,10000)

#PDF
hist, bin_edges = np.histogram(arr)
width = (bin_edges[1] - bin_edges[0]) * 0.6
plt.bar(bin_edges[1:], hist/max(hist), width=width, color='#5B9BD5')

#CDF
cdf = np.cumsum(hist/sum(hist))
plt.plot(bin_edges[1:], cdf, '-*', color='#ED7D31')

plt.title("Normal PMF&CDF")
plt.xlim([-4,4])
plt.ylim([0,1])