Linear_algebra_06_二次型
一、二次型


即使A不是对称矩阵我们也可以写成这样的形式:f(x1,x2...xn) = XTAX。
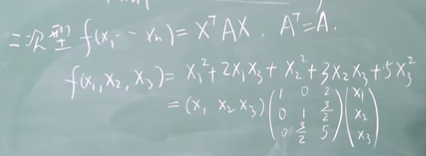
但我们保证二次型与矩阵的唯一性,所以我要求二次型的矩阵一定是对称阵。
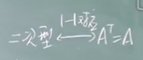



等价指的是B=PAQ,而合同指的是B=PTAP,等价不能保证P与Q是互为转置关系。
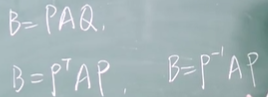
一般而言相似与合同没有关系。只有当P的转置与P的逆是相同的,及正交相似或正交合同的情况下,相似与合同一直。



二、正交变化法化二次型为标准型


n元二次型f(x1,x2...xn),我们做一个可逆线性变换,X=CY=> YT(CTAC)Y,,将二次型化为标准型 YTΛY。 实际上是CTAC=Λ 对角阵。所以说化二次型为标准型的问题,就是找可逆矩阵C,使得CTAC=Λ,也是让A与对角阵Λ合同。如果A是实对称的,那么它一定与对角阵正交相似。正交相似和正交合同是一致。









