Finance_Econometrics_MOOC_对外经贸

 

 

2.1 简单回归模型的定义

简单回归模型的形式

 

 

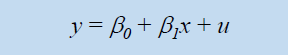
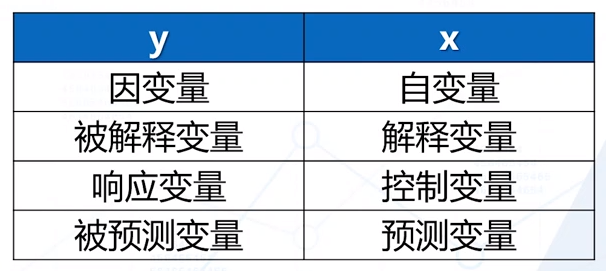
• 变量u, 称为干扰项, 代表除了x 之外其他影响 y的因素；
• b1 是斜率参数: 其他条件不变情况下， x 的边际变化所引起的y 的边际变化；
• b0截距参数。

估计过程

 

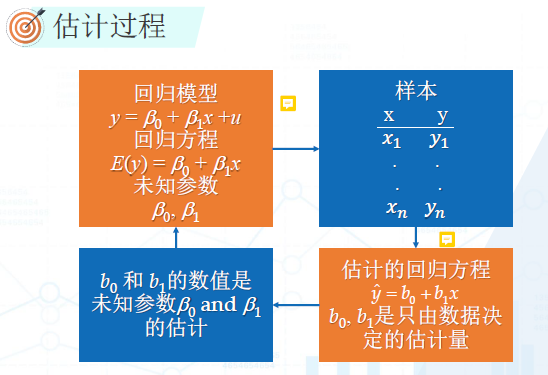
• 其中x是影响y的主要因素，而u是影响y的次要因素。E(u) = 0, 表示平均的扰动项是0.

• Xi和Yi是样本，而要估计的是Beta0和Beta1.通过最小二乘法，将Beta0和Beta1估算出来。

例子的意义

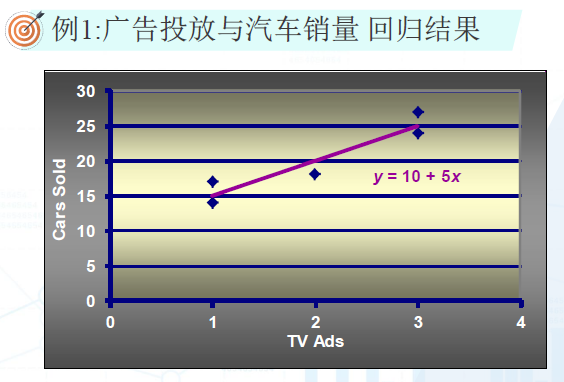
每增加一个广告投放，平均可以卖出5台车。

 每增加一名学生，班级的平均成绩就会下降2.28分。

 

2.2.1 普通最小二乘(OLS)估计量

一元线性回归模型

 

  

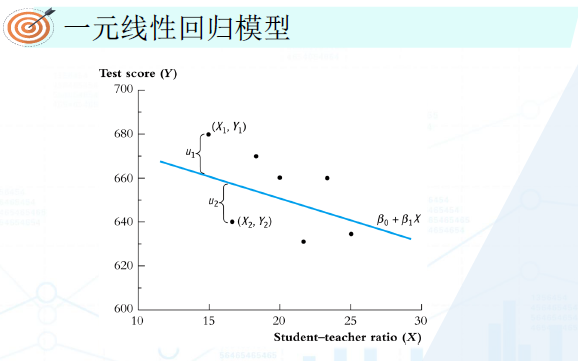
 假定我们得到一组数据，并用散点图绘制出来。我们的目的就是要拟合处一条最优的回归曲线，使得我们的每一个观察值都最靠近我们的曲线。

 

 

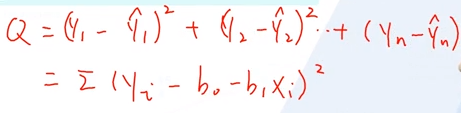
 OLS估计量的推导

 

 

 

2.2.2 矩方法

 

即便E(u)不等于0，我们也可以通过改变Beta0，使得E(u)=0.

 

E(Y)=E(Y|X)证明：  

 

 

 E(u) = E(E(u|x)), 如果E(u|x)=0，那么E(u)=E(0)=0。

若E(u|x)=0,那么u和x相对独立。Cov(x,u)=E(xu)=0

 

得出拒形式与OLS的正规方程完全相同：

 

 

 

 

2.2.4 OLS的代数性质与几何性质

 

不带常数项意思是没有Beta0.

  

 

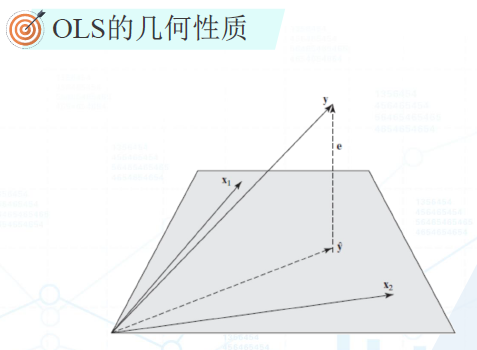
 u与x是无关的，所以u与x正交（垂直），而y_hat与x线性相关，所以y_hat在x与常数1的平面上，而y与y_hat相差u。

 

2.3.1 OLS估计量的期望

 OLS无偏性的定义

Beta1_hat的期望是关于Beta1_hat的平均行为的描述。具体到某个特别的数据Beta1，是有可能偏离我们的Beta1_hat. 

参数线性：y是关于Beta1的线性函数。

• y=B0+B1*lnx +u这是关于B1参数的线性函数
• y=B0+lnB1*x+u 这是关于x的线性函数

 

 

  

 

Beta1_hat是一个随机变量，因为ui是一个随机扰动项的线性组合。即便是同一组x，不同的ui会导致yi=B0+B1*xi+ui是不一样的。

 

 

2.3.2 OLS估计量的方差

OLS估计量𝛽1，𝛽0是随机变量，无偏性说明了它们的抽样分布是以真实参数为中心的. E(Beta_hat) = Beta

估计的参数距离真实参数有多远。度量分散程度，最常见的统计指标是方差。

同方差假设

 

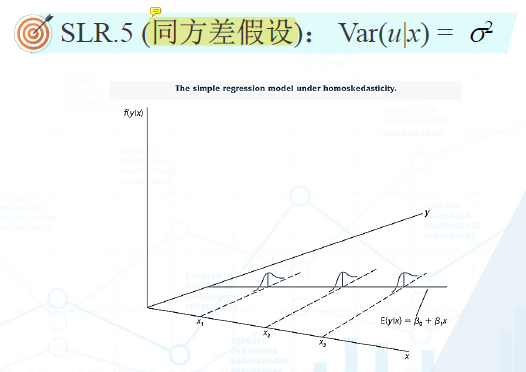
 同方差假设是指每个ui的分布的大小是一致的。

 

Var（a+bu）=b^2*var(u)

Sigma(Xi-X-) = Sigma di = Sx

 

xi的信息越丰富，我们得到的Beta1_hat就越精确。

从分子上看，Beta1的方差是跟我们Sigma相关，即与ui相关（Sigma=Var(u|x)）。u被视为噪音，u越大，Beta_hat的估计就越不精确。 

容量越大，Var(Beta_hat)方差越小。

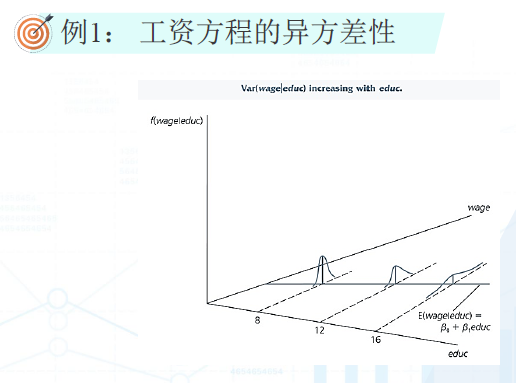
教育为8年的就业机会会更小，而教育16年的工作机会会更大。

 

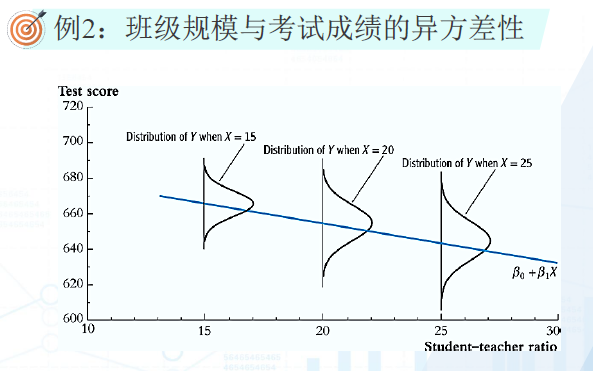
班级的生师比越大，考试成绩的差异越大。 

 

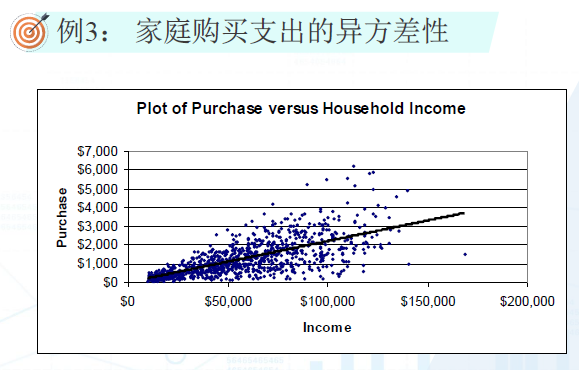
家庭收入越大，家庭支出的异方差越大。

 

在同方差中，Sigma^2是可以拿到求和式子的外边，这样可以与Sx^2约掉。
在异方差中，Sigmai是与i有关系的，就不能拿到我们求和符号外面去。