CSU-ACM2019暑假训练(2)
补题
原CF 1141F Graph Without Long Directed Paths

基本思路
染色问题,u和v记录边的两个顶点,dfs遍历。
有个问题是若边数=顶点数,为什么不能直接输出-1?
#include<bits/stdc++.h>
using namespace std;
typedef struct{
vector<int>connect;
}NODE;NODE nodes[200020];
int arr[200020];
int u[200020],v[200020];
int n,m;
bool flag=true;
void dfs(int now,int pre,int precolor)
{
arr[now]=!precolor;
if(flag)
{
for(int i=0;i<nodes[now].connect.size();i++)
{//遍历边
if(nodes[now].connect[i]==pre) continue;
if(arr[nodes[now].connect[i]]==-1)
{
dfs(nodes[now].connect[i],now,arr[now]);
}
if(arr[nodes[now].connect[i]]==arr[now])
{
flag=false;
return ;
}
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
arr[i]=-1;
for(int i=1;i<=m;i++)
{
cin>>u[i]>>v[i];
nodes[u[i]].connect.push_back(v[i]);
nodes[v[i]].connect.push_back(u[i]);
}
dfs(1,-1,0);
if(!flag)
{
cout<<"NO"<<endl;
return 0;
}
cout<<"YES"<<endl;
for(int i=1;i<=m;i++)
cout<<(arr[u[i]]==1?1:0);
return 0;
}
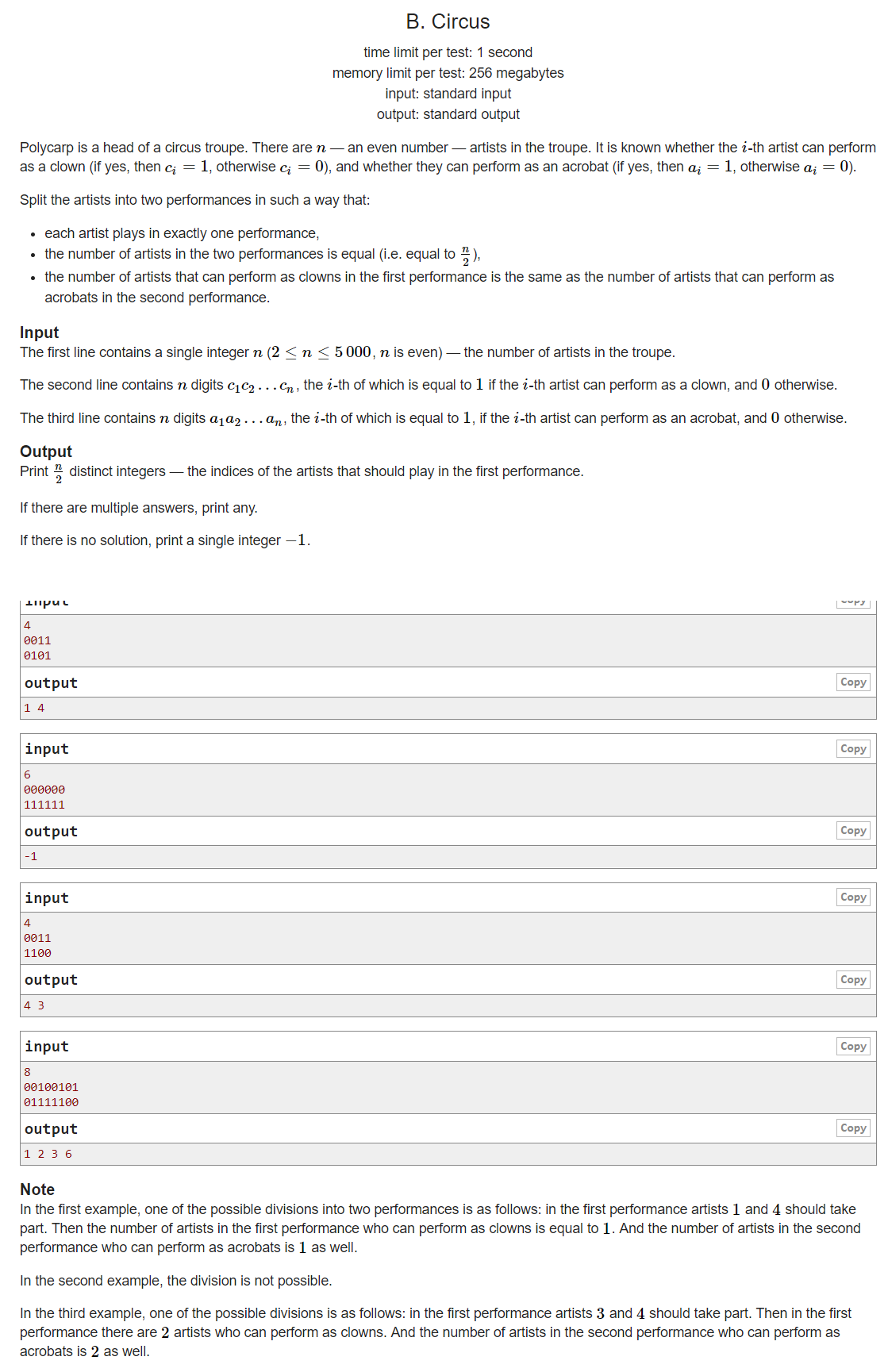
原CF 1138B Circus
基本思路
若使用排列组合,会爆tle,因为maxn=5000,设A=(0,0)的个数,B=(0,1)的个数,C=(1,0)的个数,D=(1,1)的个数,则有
\[\begin{array}{l}
A+B+C+D=n/2 \\
C+D=B.size()+D.size()-B-D
\end{array}
\]
四个未知数+两个方程组,复杂度为O(N^2),注意此题卡常,三重循环爆tle。
排列的一发tle
#include<bits/stdc++.h>
using namespace std;
typedef struct{
int a,c;
}NODE; NODE nodes[6000];
int arr[6000];
int n;bool flag=false;
void dfs(int pos,int cnt1,int cnt2,int sum1,int sum2)
{
if(flag)return ;
if(cnt1==cnt2&&cnt1==n/2)
{
if(sum1==sum2)
{
for(int i=0;i<n;i++)
if(arr[i]==1)cout<<i+1<<" ";
flag=true;
cout<<endl;
return ;
}
}
if(cnt1<n/2)
{
arr[pos]=1;
sum1+=nodes[pos].a;
dfs(pos+1,cnt1+1,cnt2,sum1,sum2) ;
arr[pos]=0;
}
if(cnt2<n/2)
{
sum2+=nodes[pos].c;
dfs(pos+1,cnt1,cnt2+1,sum1,sum2);
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
char ch;cin>>ch;if(ch=='\n')cin>>ch;
nodes[i].a=ch-'0';
}
for(int i=0;i<n;i++)
{
char ch;cin>>ch;if(ch=='\n')cin>>ch;
nodes[i].c=ch-'0';
}
dfs(0,0,0,0,0);
if(!flag)
cout<<-1<<endl;
return 0;
}
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef struct{
int a,c;
}NODE; NODE nodes[6000];
int arr[6000],sum1,sum2;
vector<int>a,b,c,d;
int n;bool flag=false;
void print(int i,int j ,int k,int h)
{
for(int x=0;x<i;x++)
{
cout<<a[x]<<" ";
}
for(int x=0;x<j;x++)
{
cout<<b[x]<<" ";
}
for(int x=0;x<k;x++)
{
cout<<c[x]<<" ";
}
for(int x=0;x<h&&x<d.size();x++)
{
cout<<d[x]<<" ";
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
char ch;cin>>ch;if(ch=='\n')cin>>ch;
nodes[i].a=ch-'0';
}
for(int i=0;i<n;i++)
{
char ch;cin>>ch;if(ch=='\n')cin>>ch;
nodes[i].c=ch-'0';
}
for(int i=0;i<n;i++)
{
if(nodes[i].a==0)
{
if(nodes[i].c==0)
a.push_back(i+1);
else b.push_back(i+1);
}
else
if(nodes[i].c==0)
c.push_back(i+1);
else d.push_back(i+1);
}
for(int i=0;i<=a.size();i++)
{
if(flag)break;
for(int j=0;j<=b.size();j++)
{
if(flag)break;
int k=n-2*i-j-b.size()-d.size();
int h=b.size()+d.size()-n/2+i;
if (h<0||h>d.size()||k<0||k>c.size()||(i+j+k+h)!=n/2)continue;
sum1=k+h;sum2=b.size()+d.size()-j-h;
if(sum1==sum2)
{
print(i,j,k,h);
flag=true;
}
}
}
if(!flag)cout<<-1<<endl;
return 0;
}
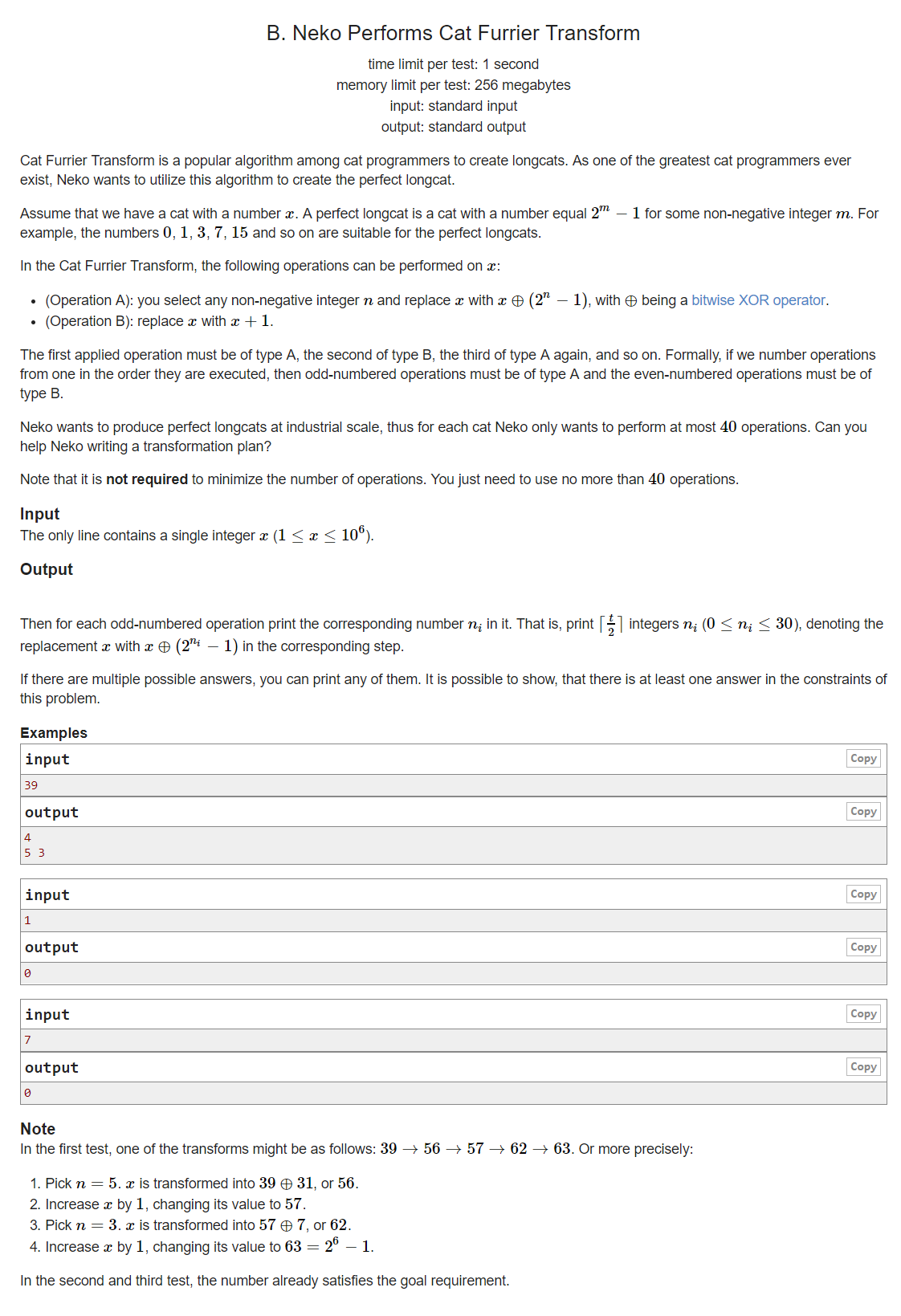
原CF 1152B
基本思路
位操作 \(full=2^{\log{2}{x}+1}-1\),取最前的一位0,做异或运算,每做一次操作判断是否满足条件
#include<bits/stdc++.h>
using namespace std;
int x,xx,maxbit,op=0;
vector<int>q;
int main()
{
cin>>x;xx=x;
int t=40;
int full=(1<<((int)log2(x)+1))-1;
while(t--)
{
maxbit=0;
int step=0;
if(xx==full)break;
while(x>1)
{
step++;
if((x&1)==0) maxbit=step;
x=x>>1;
}
op++;
q.push_back(maxbit);
int y=(1<<maxbit)-1;
xx=xx^y;
x=xx;
if(xx==full)break;
while(x>1)
{
step++;
if((x&1)==0) maxbit=step;
x=x>>1;
}
op++;
xx=xx+1;
x=xx;
}
cout<<op<<endl;
for(int i=0;i<q.size();i++)
cout<<q[i]<<" ";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号