卡特兰数
递推式
应用
二叉树个数
\(n\)个结点的二叉树个数。
\(f_0 = 1\)
当\(n \ge 1\)，枚举根结点有\(i\)个左儿子，那就有\(n - i - 1\)个右儿子，根据加法原理和乘法原理，\(f_i = \sum\limits_{i = 0}^{n - 1} f_i \times f_{n - i - 1}\)。
这和卡特兰数递推公式是一样的。
括号序列个数
\(n\)对括号的合法括号序列个数。
\(f_0 = 1\)
当\(n \ge 1\)，合法括号序列的第一个元素一定是左括号，那么就有与之配对的右括号，那么它们都可也写成\((A)B\)的形式，\(A, B\)都为合法的括号序列，那我们枚举\(A\)中的括号对数，根据加法原理和乘法原理，有\(f_n = \sum\limits_{i = 0}^{n - 1} f_i \times f_{n - i - 1}\)。
这和卡特兰数递推公式也是一样的。
出栈序列个数
其实它和括号序列是等价的，进栈相当于左括号，出栈相当于右括号。
凸多边形三角划分个数
将一个凸\(n\)多边形划分成\(n - 2\)个三角形的方案数。
\(f_3 = 1\)，为了方便计算，我们假设\(f_2 = 1\)。
当\(n > 3\)，不失一般性的，我们随意选择一条边，这条边一定是某个三角形上的一条边，枚举这个三角形的第3个点，根据加法原理和乘法原理，有\(f_n = \sum\limits_{i = 3}^{n} f_{i - 1} \times f_{n - i + 2}\)
令\(h_{n} = f_{n + 2}\)，则有\(h_n = \sum\limits_{i = 0}^{n - 1} h_{i} \times h_{n - i - 1}\)
这和卡特兰数递推公式也是一样的。
组合意义下的通项公式
用括号序列去证明。
要求对于任意前缀，左括号数量大于等于右括号数量。
我们把括号序对应到坐标上，每放一个左括号，就向上走一步，每放一个右括号，就向右走一步。
如下如：
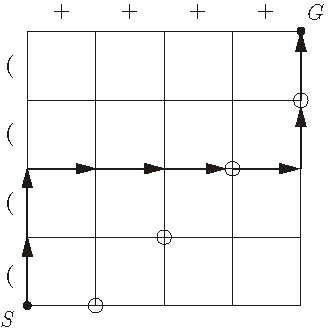
显然，一个括号序列（左右括号数量合法的括号序列）就是一条从S到G的路径。如果这条路径不经过图中的圆圈，那么它对应的括号序列就是合法的。
这总共有\(\binom{2n}{n}\)个。
接下来我们应该把其中不合法的减掉。
任意一条不合法的路径至少经过一个圆圈。
对于一条这样的路径，当它经过圆圈后，我们把它的路径对所有圆圈所在直线作对称，也就是说，当它经过圆圈后，它原本向右就变成向上，原本向上就变成向右。
如下图：
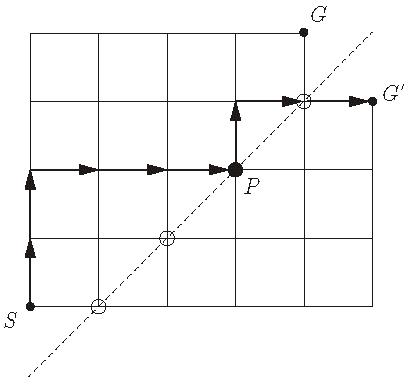
显然，任意条S到G'的路径都对应了一个不合法的括号序列，任意一个不合法的括号序列都对应了一条S到G'的路径，所以不合法的括号序列是\(\binom{2n}{n + 1}\)。
所以卡特兰数的通向公式就是\(C_n = \binom{2n}{n} - \binom{2n}{n + 1} = \frac{1}{n + 1} \binom{2n}{n}\)。
