bzoj 1001 狼抓兔子 平面图最小割
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=1001
题意:给出一张平面图。左上角点为(1,1),右下角点为(N,M)。有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下解(N,M)的窝中去。如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,才能完全封锁这条道路。求最少需要多少只狼参与伏击。
思路:
直接看就是和URAL1277相似的,但是权在边上的,直接求按原图求最小割就可以了。但是注意到N和M最大都可以到达1000。
那么直接求就会有1000*1000多个点,直接网络流显然是无法通过的。
解法参考了周冬的《两极相通——浅析最大—最小定理在信息学竞赛中的应用》
平面图有性质:
1.(欧拉公式)如果一个连通的平面图有n个点,m条边和f个面,那么f=m-n+2
2. 每个平面图G都有一个与其对偶的平面图G*, G*中的每个点对应G中的一个面,对于G中的每条边e e属于两个面f1、f2,加入边(f1*, f2*)。
而平面图G与其对偶图G*,G的面数等于G*的点数,G*的点数等于G的面数,G与G*边数相同 G*中的环对应G中的割一一对应。
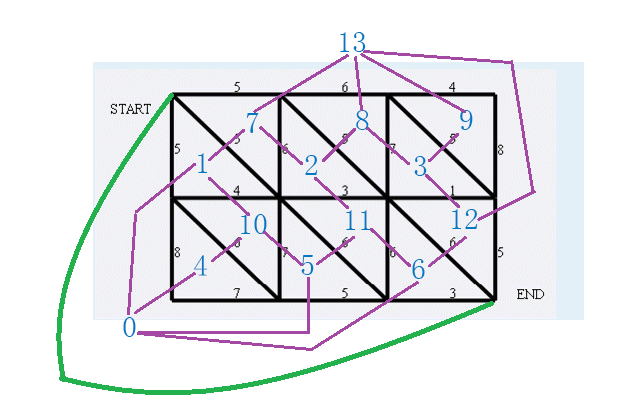
如图,把s和t连起来,形成一个附加面0,把0设为G*的s,13设为G*的t,去掉0和13之间的边。
然后用堆优化的dijkstra求s到t的最短路就可以了,用spfa也可以做。
要注意的是当N=1或者M=1的时候需要特判一下。
1 //#include <bits/stdc++.h> 2 #include <iostream> 3 #include <cstring> 4 #include <cstdio> 5 #include <queue> 6 #include <algorithm> 7 #include <vector> 8 using namespace std; 9 #define maxn 2000010 10 #define inf 0x3f3f3f3f 11 struct Edge 12 { 13 int to, val, next; 14 }edges[maxn*3]; 15 struct HeapNode 16 { 17 int d, u; 18 HeapNode(int dd, int uu){d = dd; u = uu;} 19 bool operator < (const HeapNode& rhs) const 20 { 21 return d > rhs.d; 22 } 23 }; 24 int s, t; 25 int cnt; 26 int head[maxn]; 27 void AddEdge(int from, int to, int val) 28 { 29 edges[cnt].to = to; 30 edges[cnt].val = val; 31 edges[cnt].next = head[from]; 32 head[from] = cnt++; 33 34 edges[cnt].to = from; 35 edges[cnt].val = val; 36 edges[cnt].next = head[to]; 37 head[to] = cnt++; 38 } 39 int N, M; 40 int d[maxn], vis[maxn]; 41 void dijkstra() 42 { 43 priority_queue <HeapNode> q; 44 for(int i = s; i <= t; i++) d[i] = inf; 45 d[s] = 0; 46 memset(vis, 0, sizeof(vis)); 47 q.push(HeapNode(0, s)); 48 while(!q.empty()) 49 { 50 HeapNode x = q.top(); q.pop(); 51 int u = x.u; 52 if(vis[u]) continue; 53 vis[u] = 1; 54 for(int i = head[u]; i != -1; i = edges[i].next) 55 { 56 Edge &e = edges[i]; 57 if(d[e.to] > d[u] + e.val) 58 { 59 d[e.to] = d[u] + e.val; 60 q.push(HeapNode(d[e.to], e.to)); 61 } 62 } 63 } 64 printf("%d\n", d[t]); 65 } 66 int main() 67 { 68 // freopen("in.txt", "r", stdin); 69 // freopen("out.txt", "w", stdout); 70 while(~scanf("%d%d", &N, &M)) 71 { 72 if(N == 1 || M == 1) 73 { 74 int ans = inf; 75 if(N == 1 && M == 1){printf("0\n"); continue;} 76 int w; 77 for(int i = 1; i <= N; i++) for(int j = 1; j <= M-1; j++) 78 { 79 scanf("%d", &w); ans = min(ans, w); 80 } 81 for(int i = 1; i <= N-1; i++) for(int j = 1; j <= M; j++) 82 { 83 scanf("%d", &w); ans = min(ans, w); 84 } 85 printf("%d\n", ans); continue; 86 } 87 cnt = 0; int w; 88 memset(head, -1, sizeof(head)); 89 s = 0; t = (N-1)*(M-1)*2+1; 90 int add = (N-1)*(M-1); 91 for(int i = 1; i <= N; i++) 92 { 93 for(int j = 1; j <= M-1; j++) 94 { 95 scanf("%d", &w); 96 if(i == 1) AddEdge(t, (i-1)*(M-1)+j+add, w); 97 else if(i == N) AddEdge(s, (i-2)*(M-1)+j, w); 98 else AddEdge((i-2)*(M-1)+j, (i-1)*(M-1)+j+add, w); 99 } 100 } 101 for(int i = 1; i <= N-1; i++) 102 { 103 for(int j = 1; j <= M; j++) 104 { 105 scanf("%d", &w); 106 if(j == 1) AddEdge(s, (i-1)*(M-1)+j, w); 107 else if(j == M) AddEdge(t, (i-1)*(M-1)+j-1+add, w); 108 else AddEdge((i-1)*(M-1)+j-1+add, (i-1)*(M-1)+j, w); 109 } 110 } 111 for(int i = 1; i <= N-1; i++) 112 { 113 for(int j = 1; j <= M-1; j++) 114 { 115 scanf("%d", &w); 116 AddEdge((i-1)*(M-1)+j, (i-1)*(M-1)+j+add, w); 117 } 118 } 119 dijkstra(); 120 121 } 122 return 0; 123 }




