算法分析实践大作业

1. 问题

    给定n个大小不等的圆c1,c2,…,cn，现要将这n个圆排进一个矩形框中，且要求各圆与矩形的底边相切。圆排列问题要求从n个圆的所有排列中找出由最小长度的圆排列。

2. 解析

  这个问题可以通过搜索求出圆的全排列，并且计算排列中每个圆圆心所在横坐标的位置，每个圆心所在的x坐标减去其半径来更新左端点，加上半径来更新右端点，右端点减去左端点来更新最小值，最后的答案就是最优值

 

下面是排列树的图形

 

 

 

我们可以通过下面两张图发现，最新的圆所在横坐标，并不一定是与他最近的圆所决定的，我们需要判断其与之前所有排列的圆相切之后，最靠右的横坐标，这才是其横坐标

 

 

 

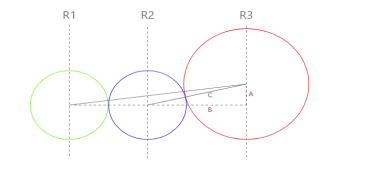
同时我们发现

设X为新的圆的横坐标，Y为之前排列的某一个圆的横坐标,设Y所在圆半径为R1，X所在圆半径为R2

X=Y+sqrt((R1+R2)*(R1+R2)-(R1-R2)*(R1-R2));

化简后可得 X=Y+2.0*sqrt(R1*R2)

    

 

 

3. 设计

   计算当前圆横坐标

   

double cal_center(int t){
    double centerx=0;
    for(int i=0;i<t;i++){//取之前排列圆里面相切最大的x坐标，其余计算出来的坐标必定和之前某个圆的相交 
        centerx=max(centerx,center[i]+2.0*sqrt(r[t]*r[i]));
    }
    return centerx;
}

 

  计算最后的长度

 

void cal(){//计算此排列下矩形长度 
    double left=0,right=0;
    for(int i=0;i<n;i++){
        left=min(left,center[i]-r[i]);
        right=max(right,center[i]+r[i]);
    }
    if(ans>right-left) {
        ans=right-left;
        for(int i=0;i<n;i++) dos[i]=r[i];
    }
    return;
}

 

 

 回溯法求搜索树

 

for(int i=x;i<n;i++){//回溯法排列树 
          swap(r[x],r[i]);
          double y=cal_center(x);
          if(y+r[1]+r[x]<ans) center[x]=y,dfs(x+1);//剪枝，若此时 圆心加半径的长度已经比最小长度大则没必要继续搜索 
          swap(r[x],r[i]);
     }

 

 

4. 分析

对于搜索树其复杂度为O(n!)

最后计算长度需要O(n)

则其复杂度为O(n*n!)

5. 源码

#include <stdlib.h>
#include <time.h>
#include<stdio.h>
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bitset>
#include<set>
#include<deque>
#include<queue>
#include<vector>
//#include<unordered_map>
#include<map>
#include<stack>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define Pii pair<ll,int>
#define m_p make_pair
#define l_b lower_bound
#define u_b upper_bound
const int inf = 0x3f3f3f3f;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const int maxn = 2e5 + 11;
const int maxm = 20;
const int mod = 1000000007;
const double eps = 1e-5;
inline ll rd() { ll x = 0, f = 1; char ch = getchar(); while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f; }
inline ll qpow(ll a, ll b, ll p) { ll res = 1; while (b) { if (b & 1) { res *= a; res %= p; }b >>= 1; a = a * a%p; }return res; }
inline ll gcd(ll a, ll b) { if (b == 0) return a; return gcd(b, a%b); }
//template<class T> void read(T&num) { char CH; bool F = false; for (CH = getchar(); CH<'0' || CH>'9'; F = CH == '-', CH = getchar()); for (num = 0; CH >= '0'&&CH <= '9'; num = num * 10 + CH - '0', CH = getchar()); F && (num = -num); }
//void print(__int128 x) { if (x < 0) { putchar('-'); x = -x; }if (x > 9) print(x / 10); putchar(x % 10 + '0'); }
//iterator
//head
//priority_queue
//高斯消元  
double ans,center[maxm];//center[maxm]全排列时指每个圆的圆心坐标 
int n,r[maxm],dos[maxm]; 
void cal(){//计算此排列下矩形长度 
    double left=0,right=0;
    for(int i=0;i<n;i++){
        left=min(left,center[i]-r[i]);
        right=max(right,center[i]+r[i]);
    }
    if(ans>right-left) {
        ans=right-left;
        for(int i=0;i<n;i++) dos[i]=r[i];
    }
    return;
}
double cal_center(int t){
    double centerx=0;
    for(int i=0;i<t;i++){//取之前排列圆里面相切最大的x坐标，其余计算出来的坐标必定和之前某个圆的相交 
        centerx=max(centerx,center[i]+2.0*sqrt(r[t]*r[i]));
    }
    return centerx;
}
void dfs(int x)
{
    if(x==n){
        cal();
        return;
    }
    for(int i=x;i<n;i++){//回溯法排列树 
          swap(r[x],r[i]);
          double y=cal_center(x);
          if(y+r[1]+r[x]<ans) center[x]=y,dfs(x+1);//剪枝，若此时 圆心加半径的长度已经比最小长度大则没必要继续搜索 
          swap(r[x],r[i]);
     }
}
int main()
{
    n=rd();
    ans=inf;
    for(int i=0;i<n;i++) r[i]=rd();
//    sort(r,r+n,greater<int>()); 感觉有序无序对于剪枝影响不大 
    dfs(0);
    printf("%lf\n",ans);
    for(int i=0;i<n;i++) printf("%d ",dos[i]);//输出半径排列 
    puts("");
    return 0;
}

 

https://github.com/Tinkerllt/algorithm-work.git