算法分析第五次作业

1. 问题

  在包含有n个点的集合S中，找出距离最近的两个点。设 p1(x1,y1)，p2(x2,y2)，……，pn(xn,yn)是平面的n个点。 严格地将，最近点对可能不止一对，此例输出一对即可。

2. 解析

  我们先根据x坐标排序，进行递归算出每一部分的距离，在根据y坐标排序计算每一部分之间的最近距离，最后得到答案。

同时我们在进行第二部分计算的时候，通过鸽舍原理易知，最多需要计算距离中心点y坐标最近的6个点来得到答案。

3. 设计

    在利用分治法思想解决此问题时，首先考虑将最近对问题进行分治，设计其分治策略。将集合S分成两个子集S1和S2，根据平衡子问题原则，每个子集中的点数大致都为n/2。这样分治后，最近点对将会出现三种情况：在S1中，在S2中或者最近点对分别在集合S1和S2中。利用递归分析法分别计算前两种情况，第三种方法另外分析。求解出三类子情况后，再合并三类情况，比较分析后输出三者中最小的距离。

4. 分析

 

 

 

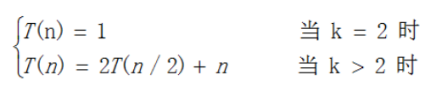
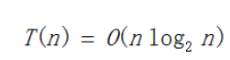
5. 源码

https://github.com/Tinkerllt/algorithm-work.git

  1 #include <iostream>
  2 #include <string>
  3 #include <vector>
  4 #include <algorithm>
  5 #include <cmath>
  6 #include <cstdlib>
  7 #include <ctime>
  8 #include <iomanip>
  9 using namespace std;
 10 const int maxn = 0x3f3f3f3f;
 11 struct Point
 12 {
 13     int x,y;
 14     friend ostream & operator << (ostream & out,const Point& p);
 15     Point(int _x=0,int _y=0):x(_x),y(_y){}
 16     bool operator < (const Point& rhs)const{
 17         return x < rhs.x;
 18     }
 19 };
 20 ostream & operator << (ostream & out,const Point& p){
 21     out<<"("<<setw(2)<<p.x<<","<<setw(2)<<p.y<<")";
 22     return out;
 23 }
 24 bool cmp(const Point&a,const Point&b) //按x坐标排序
 25 {
 26     return a.x<b.x;
 27 }
 28 bool cmp2(const Point&a,const Point&b) //按y坐标排序
 29 {
 30     return a.y<b.y;
 31 }
 32 
 33 double Dis(Point a,Point b)
 34 {
 35     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 36 }
 37 double min(double a,double b,double c)
 38 {
 39     return min(min(a,b),c));  
 40 }
 41 
 42 double ClosestPoint(vector<Point> points,int m,int n)  //左闭右开
 43 {
 44     if(n-m<2) return maxn;
 45     if(n-m==2)
 46     {
 47         return Dis(points[m],points[n-1]);
 48     }
 49     if(n-m==3)
 50     {
 51         double a = Dis(points[m],points[n-1]);
 52         double b = Dis(points[m],points[n-2]);
 53         double c = Dis(points[n-1],points[n-2]);
 54         return min(a,b,c);
 55     }
 56     int mid = (m+n)/2;
 57     int mm = points[mid].x;
 58 
 59     double d1 = ClosestPoint(points,m,mid); // 左边区域最短距离
 60     double d2 = ClosestPoint(points,mid,n);  // 右边区域最短距离
 61     double minn = min(d1,d2);
 62     vector<Point> left,right;
 63     for(int i=m;i<mid;++i)
 64     {
 65         if(points[i].x>mm-minn)
 66             left.push_back(points[i]);
 67     }
 68     for(int i=mid;i<n;++i)
 69     {
 70         if(points[i].x<=mm+minn)
 71             right.push_back(points[i]);
 72     }
 73     sort(right.begin(),right.end(),cmp2); //按y坐标排序
 74     double mindist = 100000;
 75     for(int i=0;i<(int)left.size();i++)   //遍历左边所有点求与右边最短距离
 76     {
 77         for(int j=0;j<(int)right.size();j++)
 78         {
 79             if(abs(left[i].y-right[j].y)<minn)
 80             {
 81                 double d = Dis(left[i],right[j]);
 82                 if(d<min) mindist = d;
 83             }
 84         }
 85     }
 86     return min(minn,mindist);
 87 }
 88 int main()
 89 {
 90     //freopen("out.txt","w",stdout);
 91     vector<Point> points;
 92     srand(time(NULL));
 93     int n = 15;
 94     for(int i=0;i<n;i++)
 95     {
 96         Point point;
 97         point.x = rand()%71;
 98         point.y = rand()%61;
 99     //    cin>>point.x>>point.y;
100         points.push_back(point);
101     }
102     sort(points.begin(),points.end(),cmp);
103     for(int i=0;i<n;i++)
104     {
105         //cout << points[i].x <<" "<< points[i].y <<endl;
106         cout<<points[i]<<endl;
107     }
108     cout << "分治法求得的答案为："<< ClosestPoint(points,0,points.size()) << endl ;
109     return 0;
110 }
View Code

 

posted @ 2020-03-31 14:16  Tinker1998  阅读(155)  评论(0)  编辑  收藏  举报