算法分析第一次作业
最小生成树算法:Kruskal算法rime算法的分析
题目来源:https://vjudge.net/problem/HDU-1863
问题
什么是最小生成树(MST)
1.边的权重和最小
2.|V|个顶点一定有|V|-1条边,并构成连通图
解析
Kruskal
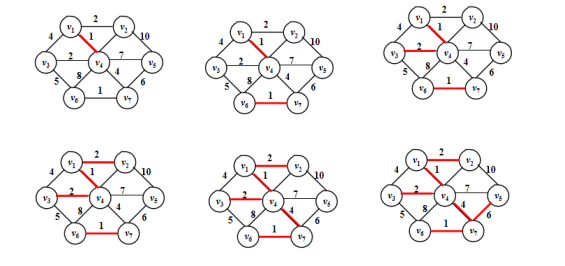
prime
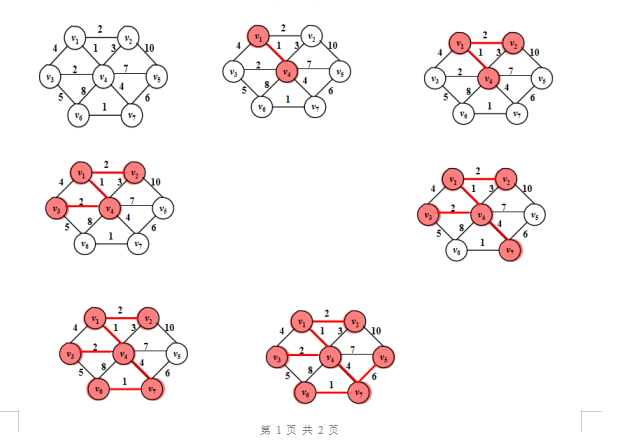
设计
Kruskal:核心思想就是贪心的加入边,我们将边权值从小到大排序,然后遍历每一条边,判断当前边链接的两个点是否已经联通(是否加入最小生成树图),若不连通则将此条边加入图,我们可以知道若这条边链接的两个两点并不联通那么这条就是联通这两个点的最小代价,所以他必定在图中所以这个算法是合理的
Prime:核心思想是随机选取一个起点,贪心选择这个点所连的最小边,将这点就如最小生成树图,并使用这条边松弛别的边,重复这个过程。
分析
n为点数,m为边数
Kruskal:m*logm
Prime:n*n

1 #include<stdio.h> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #include<bitset> 7 #include<set> 8 #include<deque> 9 #include<queue> 10 #include<vector> 11 //#include<unordered_map> 12 #include<map> 13 #include<stack> 14 using namespace std; 15 #define ll long long 16 #define ull unsigned long long 17 #define pii pair<int,int> 18 #define Pii pair<ll,ll> 19 #define m_p make_pair 20 #define l_b lower_bound 21 #define u_b upper_bound 22 const int inf = 0x3f3f3f3f; 23 const ll linf = 0x3f3f3f3f3f3f3f3f; 24 const int maxn = 3e5 + 11; 25 const int maxm = 2e3 + 11; 26 const int mod = 1e9 + 7; 27 const double eps = 1e-5; 28 ll rd() { ll x = 0, f = 1; char ch = getchar(); while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f; } 29 inline ll qpow(ll a, ll b) { ll res = 1; while (b) { if (b & 1) { res *= a; res %= mod; }b >>= 1; a = a * a%mod; }return res; } 30 inline ll gcd(ll a, ll b) { if (b == 0) return a; return gcd(b, a%b); } 31 //iterator 32 //head 33 int fa[maxn], n, m, ans; 34 struct node { 35 int from, to, val; 36 bool operator <(const node &a) { 37 return this->val < a.val; 38 } 39 }tree[maxn]; 40 int find(int x) { 41 return fa[x] == x ? x : fa[x] = find(fa[x]); 42 } 43 void merge(int x, int y) { 44 fa[find(x)] = find(y); 45 } 46 bool same(int x, int y) { 47 return find(x) == find(y); 48 } 49 void Kruskal() { 50 ans = 0; 51 for (int i = 1; i <= m; i++) { 52 if (same(tree[i].from, tree[i].to)) continue; 53 ans += tree[i].val; 54 merge(tree[i].from, tree[i].to); 55 } 56 int count = 0; 57 for (int i = 1; i <= n; i++) { 58 if (find(i) == i) ++count; 59 } 60 if (count > 1) ans = -1; 61 } 62 void init() { 63 for (int i = 1; i <= n; i++) { 64 fa[i] = i; 65 } 66 } 67 int main() { 68 while (cin>>m && m != 0) { 69 n = rd(); 70 init(); 71 for (int i = 1; i <= m; i++) { 72 tree[i].from = rd(); 73 tree[i].to = rd(); 74 tree[i].val = rd(); 75 } 76 sort(tree + 1, tree + m + 1); 77 Kruskal(); 78 if (ans == -1) cout << "?" << '\n'; 79 else cout << ans << '\n'; 80 } 81 }

1 #include<stdio.h> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #include<bitset> 7 #include<set> 8 #include<deque> 9 #include<queue> 10 #include<vector> 11 //#include<unordered_map> 12 #include<map> 13 #include<stack> 14 using namespace std; 15 #define ll long long 16 #define ull unsigned long long 17 #define pii pair<int,int> 18 #define Pii pair<ll,ll> 19 #define m_p make_pair 20 #define l_b lower_bound 21 #define u_b upper_bound 22 const int inf = 0x3f3f3f3f; 23 const ll linf = 0x3f3f3f3f3f3f3f3f; 24 const int maxn = 3e6 + 11; 25 const int maxm = 2e3 + 11; 26 const int mod = 1e9 + 7; 27 const double eps = 1e-5; 28 ll rd() { ll x = 0, f = 1; char ch = getchar(); while (ch<'0' || ch>'9') { if (ch == '-')f = -1; ch = getchar(); }while (ch >= '0'&&ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }return x * f; } 29 inline ll qpow(ll a, ll b) { ll res = 1; while (b) { if (b & 1) { res *= a; res %= mod; }b >>= 1; a = a * a%mod; }return res; } 30 inline ll gcd(ll a, ll b) { if (b == 0) return a; return gcd(b, a%b); } 31 //iterator 32 //head 33 int vis[maxm], n, m, ans; 34 int mp[maxm][maxm],dis[maxm]; 35 void Prime(int cur) { 36 ans = 0; 37 vis[cur]=1; 38 for(int i=1;i<=n;i++){ 39 dis[i]=mp[cur][i]; 40 } 41 for (int i = 1; i < n; i++) { 42 int minn=inf,index; 43 for(int j=1;j<=n;j++){ 44 if(!vis[j]&&dis[j]<minn){ 45 minn=dis[j]; 46 index=j; 47 } 48 } 49 if(minn==inf) { 50 ans=-1; 51 return; 52 } 53 vis[index]=1; 54 ans+=minn; 55 for(int j=1;j<=n;j++){ 56 if(!vis[j]&&mp[index][j]<dis[j]){ 57 dis[j]=mp[index][j]; 58 } 59 } 60 } 61 for (int i = 1; i <= n; i++) { 62 if (!vis[i]) ans=-1; 63 } 64 } 65 void init(){ 66 for(int i=1;i<=n;i++) dis[i]=inf,vis[i]=0; 67 memset(mp,inf,sizeof mp); 68 } 69 int main() { 70 while (cin>>m && m != 0) { 71 n = rd(); 72 init(); 73 for (int i = 1; i <= m; i++) { 74 int x=rd(),y=rd(),v=rd(); 75 if(mp[x][y]>v){ 76 mp[x][y]=v; 77 mp[y][x]=v; 78 } 79 } 80 Prime(1); 81 if (ans == -1) cout << "?" << '\n'; 82 else cout << ans << '\n'; 83 } 84 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号