树上任意两点间距离

//  

任意两点间有唯一路径的无向图是树

 

//HDU   6446

Tree and Permutation

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1192    Accepted Submission(s): 432

Problem Description

There are N vertices connected by N−1 edges, each edge has its own length.
The set { 1,2,3,…,N } contains a total of N! unique permutations, let’s say the i-th permutation is Pi and Pi,j is its j-th number.
For the i-th permutation, it can be a traverse sequence of the tree with N vertices, which means we can go from the Pi,1-th vertex to the Pi,2-th vertex by the shortest path, then go to the Pi,3-th vertex ( also by the shortest path ) , and so on. Finally we’ll reach the Pi,N-th vertex, let’s define the total distance of this route as D(Pi) , so please calculate the sum of D(Pi) for all N! permutations.

 

 

Input

There are 10 test cases at most.
The first line of each test case contains one integer N ( 1≤N≤105 ) .
For the next N−1 lines, each line contains three integer X, Y and L, which means there is an edge between X-th vertex and Y-th of length L ( 1≤X,Y≤N,1≤L≤109 ) .

 

 

Output

For each test case, print the answer module 109+7 in one line.

 

 

Sample Input

3 1 2 1 2 3 1 3 1 2 1 1 3 2

 

 

Sample Output

16 24

 

 

 

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <string>
#include <deque>
using namespace std;
#define  ll long long 
#define  N 100009
#define  mod  1000000007
#define  gep(i,a,b)  for(int  i=a;i<=b;i++)
#define  gepp(i,a,b) for(int  i=a;i>=b;i--)
#define  gep1(i,a,b)  for(ll i=a;i<=b;i++)
#define  gepp1(i,a,b) for(ll i=a;i>=b;i--)    
#define  mem(a,b)  memset(a,b,sizeof(a))
#define  lowbit(x) x&(-x)
int n,head[N],cnt;
ll sum[N];
ll ret,ans;
ll  f[N];
struct M{
    int u,v,w,nex;
}e[N<<1];//无向图*2，易错。
void add(int u,int v,int w){
    e[cnt].u=u;
    e[cnt].v=v;
    e[cnt].w=w;
    e[cnt].nex=head[u];
    head[u]=cnt++;
}
void dfs(int u,int fa)
{
    sum[u]=1ll;
    for(int i=head[u];i!=-1;i=e[i].nex){
        int v=e[i].v;
        int w=e[i].w;
        if(v==fa) continue;
        dfs(v,u);
        sum[u]+=sum[v];
        /*
        我们可以对每条边，求所有可能的路径经过此边的次数：
        设这条边两端的点数分别为A和B，那么这条边被经过的次数就是A*B，
        它对总的距离和的贡献就是(A*B*此边长度)。
        */
        ret=(ret+sum[v]*(n-sum[v])%mod*w%mod)%mod;
    }
}
void init()
{
    f[0]=1ll;
    gep(i,1,N){
        f[i]=(f[i-1]*i)%mod;
    }
}
int main()
{
    init();
    while(~scanf("%d",&n)){
        cnt=0;
        int u,v,w;
        mem(head,-1);
        mem(sum,0);
        gep(i,1,n-1){
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
            add(v,u,w);//必须无向图
        }
        ret=0;
        dfs(1,0);
        /*
        (n-1)*n!/(C(n,2)) =2*(n-1)! 
        如 
            1 2 3
            1 3 2
            2 1 3 
            2 3 1
            3 1 2
            3 2 1
         (1,2) ,(1,3) ,(2,3) 都有4次(2*2!) 
         而走完一次 (1,2) ,(1,3) ,(2,3)需要的花费(即树上任意两点的路径都走一次)
         为 ret ，那么ret*2*(n-1)!就是答案
        */
        ans=2*ret%mod*f[n-1]%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

 

 

//HDU  2376

Average distance

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1327    Accepted Submission(s): 479
Special Judge

Problem Description

Given a tree, calculate the average distance between two vertices in the tree. For example, the average distance between two vertices in the following tree is (d₀₁ + d₀₂+ d₀₃ + d₀₄ + d₁₂ +d₁₃ +d₁₄ +d₂₃ +d₂₄ +d₃₄)/10 = (6+3+7+9+9+13+15+10+12+2)/10 = 8.6.

 

 

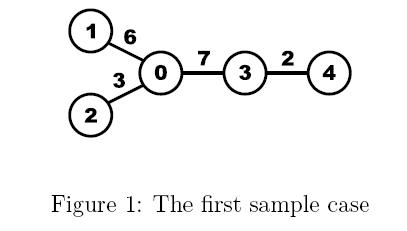
Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case: 

One line with an integer n (2 <= n <= 10 000): the number of nodes in the tree. The nodes are numbered from 0 to n - 1. 

n - 1 lines, each with three integers a (0 <= a < n), b (0 <= b < n) and d (1 <= d <= 1 000). There is an edge between the nodes with numbers a and b of length d. The resulting graph will be a tree. 

 

 

Output

For each testcase: 

One line with the average distance between two vertices. This value should have either an absolute or a relative error of at most 10^-6

 

 

Sample Input

1

5

0 1 6

0 2 3

0 3 7

3 4 2

 

Sample Output

8.6

 

 

 

int t,n;
int head[N],cnt;
double ret,ans,sum[N];
struct M{
    int u,v,w,nex;
}e[N<<1];
void  add(int u,int v,int w)
{
    e[cnt].u=u;
    e[cnt].v=v;
    e[cnt].w=w;
    e[cnt].nex=head[u];
    head[u]=cnt++;   
}
void dfs(int u,int fa)
{
    sum[u]=1;
    for(int i=head[u];i!=-1;i=e[i].nex)
    {
       int v=e[i].v;
       int w=e[i].w;
       if(v==fa) continue;
          dfs(v,u);  
       sum[u]+=sum[v];
       ret=ret+sum[v]*(n-sum[v])*w;
    }
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        mem(head,-1);
        mem(sum,0);
        cnt=0;
        int u,v,w;
        gep(i,1,n-1){
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
            add(v,u,w);
        }
        ret=0;
        dfs(0,-1);
        ans=2.0*ret/(n*(n-1)*1.0);
        printf("%.7f\n",ans);
    }
    return 0;
}