组合数的几种写法
1 //数据量较小,1000 2 void C() 3 { 4 c[0][0]=1; 5 for(int i=1;i<=10;i++) 6 { 7 for(int j=0;j<=i;j++){ 8 if(j==0||j==i) c[i][j]=1; 9 else{ 10 c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod; 11 } 12 printf("%d%c",c[i][j],j==i?'\n':' '); 13 } 14 printf("\n"); 15 } 16 } 55 // 0≤n≤1e18，0≤m≤1e6，1≤mod≤1e9，用卢卡斯定理,mod为素数 56 void egcd(ll a,ll b,ll &x,ll &y) 57 { 58 ll d; 59 if(!b) { 60 x=1,y=0; 61 return ; 62 } 63 else{ 64 egcd(b,a%b,y,x); 65 y-=(a/b)*x; 66 } 67 } 68 ll inv(ll n) 69 { 70 ll x,y; 71 egcd(n,mod,x,y); 72 return (x%mod+mod)%mod; 73 } 74 ll C(ll n,ll m) 75 { 76 if(m>n) return 0; 77 ll ans=1ll; 78 for(ll i=1;i<=m;i++) 79 { 80 ans=(ans*(n-m+i)%mod*inv(i)%mod)%mod; 81 } 82 return ans; 83 }
C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p 84 ll solve(ll n,ll m) 85 { 86 if(m==0) return 1; 87 return C(n%mod,m%mod)*solve(n/mod,m/mod)%mod; 88 } 89 90 91 //0≤m≤n≤1e18，1≤mod≤1e6，用卢卡斯定理，mod为素数 92 ll f[1000009]; 93 void init() 94 { 95 f[0]=1; 96 for(ll i=1;i<=mod;i++) 97 { 98 f[i]=(f[i-1]*i)%mod; 99 } 100 return ; 101 } 102 void egcd(ll a,ll b,ll &x,ll &y) 103 { 104 ll d; 105 if(!b){ 106 x=1,y=0; 107 return ; 108 } 109 else{ 110 egcd(b,a%b,y,x); 111 y-=(a/b)*x; 112 } 113 } 114 ll inv(ll n) 115 { 116 ll x,y; 117 egcd(n,mod,x,y); 118 return (x%mod+mod)%mod; 119 } 120 ll C(ll n,ll m) 121 { 122 ll ans=1ll; 123 while(n&&m){ 124 ll nn=n%mod,mm=m%mod; 125 if(nn<mm) return 0; 126 ans=(ans*f[nn]%mod*inv(f[mm]*f[nn-mm]%mod)%mod)%mod; 127 n/=mod; 128 m/=mod; 129 } 130 return ans; 131 }
1 //0<=n,mod<=1e6. 2 ll fac[N] = {1, 1}, inv[N] = {1, 1}, f[N] = {1, 1}; 3 ll C(ll a, ll b) { 4 if (b > a)return 0; 5 return fac[a] * inv[b] % mod * inv[a - b] % mod; 6 } 7 void init() { //快速计算阶乘的逆元，mod为素数 8 for (int i = 2; i < N; i++) { 9 fac[i] = fac[i - 1] * i % mod; 10 f[i] = (mod - mod / i) * f[mod % i] % mod; 11 inv[i] = inv[i - 1] * f[i] % mod; 12 } 13 }
1 //c(n,m)%M ：M为p[i]的乘积 2 //n,m,M都在10^18范围 3 //p[i]都是素数，且都小于10^5 4 // HDU 5446 5 #include <iostream> 6 #include <cstdio> 7 #include <cstring> 8 #include <vector> 9 #include <queue> 10 using namespace std; 11 typedef long long ll; 12 ll p[15],an[15]; 13 ll fac[100005],inv[100005]; 14 ll pow_mod(ll a, ll n, ll mod) 15 { 16 ll ret = 1; 17 while (n) 18 { 19 if (n&1) ret = ret * a % mod; 20 a = a * a % mod; 21 n >>= 1; 22 } 23 return ret; 24 } 25 void ini(int x) 26 { 27 fac[0] = 1; 28 for(int i = 1; i < x; i++) fac[i] = fac[i-1]*i%x; 29 inv[x - 1] = pow_mod(fac[x-1],x-2,x); 30 for(int i = x - 2; i >= 0; i--) inv[i] = inv[i+1] * (i+1) % x; 31 } 32 ll c(ll a,ll b,ll p) 33 { 34 if(a < b || a < 0 || b < 0) 35 return 0; 36 return fac[a]*inv[b]%p*inv[a-b]%p; 37 } 38 ll lucas(ll a,ll b, ll p) 39 { 40 if( b == 0) 41 return 1; 42 return lucas(a/p,b/p,p)*c(a%p,b%p,p)%p; 43 } 44 ll ex_gcd(ll a, ll b, ll& x, ll& y) 45 { 46 if (b == 0) 47 { 48 x = 1; 49 y = 0; 50 return a; 51 } 52 ll d = ex_gcd(b, a % b, y, x); 53 y -= x * (a / b); 54 return d; 55 } 56 ll mul(ll a, ll b, ll mod) 57 { 58 a = (a % mod + mod) % mod; 59 b = (b % mod + mod) % mod; 60 ll ret = 0; 61 while(b) 62 { 63 if(b&1) 64 { 65 ret += a; 66 if(ret >= mod) ret -= mod; 67 } 68 b >>= 1; 69 a <<= 1; 70 if(a >= mod) a -= mod; 71 } 72 return ret; 73 } 74 ll china(ll n,ll a[],ll b[]) 75 { 76 ll M = 1,d,y,x= 0; 77 for(int i = 0; i < n; i++) 78 { 79 M *= b[i]; 80 } 81 for(int i = 0; i < n; i++) 82 { 83 ll w = M/b[i]; 84 ex_gcd(b[i],w,d,y); 85 x = (x + mul(mul(y, w, M), a[i], M));//可能超范围 86 } 87 return (x+M) % M; 88 } 89 int main() 90 { 91 int t,k; 92 ll n,m; 93 scanf("%d",&t); 94 while(t--) 95 { 96 scanf("%lld%lld",&n,&m); 97 scanf("%d",&k); 98 for(int i = 0; i < k; i++) 99 { 100 scanf("%lld",&p[i]); 101 ini(p[i]); 102 an[i] = lucas(n,m,p[i]); 103 } 104 printf("%lld\n",china(k,an,p)); 105 } 106 return 0; 107 }
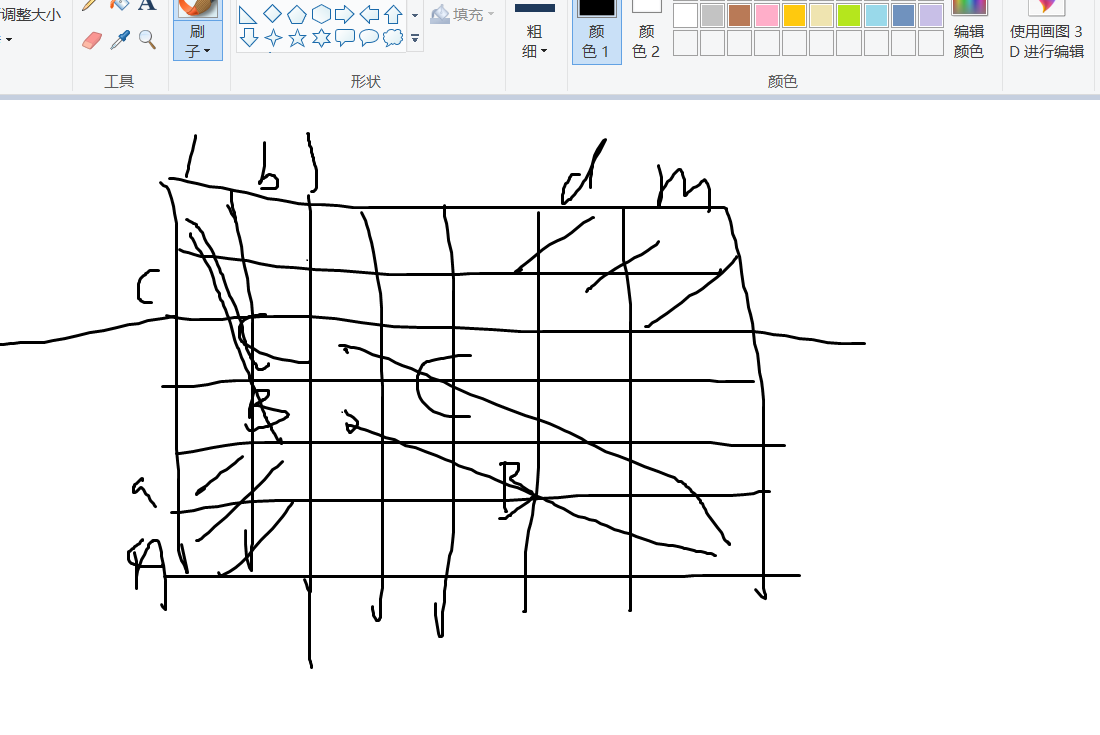
B: Interseting paths 时间限制: 1 s 内存限制: 128 MB 题目描述 给定一个n行m列的迷宫，行的编号从顶端到底部编号为1−>n，列的编号从左到右为1−>m。 现在你处于迷宫的左上角(1,1)处，现在你要到网格的(n,m)处。并且，你只能在当前的格子向右走或者向下走。即(x,y)−>(x+1,y)或者(x,y),(x,y+1)。但是，当你走到两个小矩阵内时就不能再走，这两个小矩阵分别是行a−>n,列1−>b。和行1−>c,列d,m.并且数据保证1≤c<a≤n,1≤b<d≤m. 现在，你想知道从(1,1)走到(n,m)有多少种方式。 输入 第一行一个整数t，代表有t组测试数据 接下来t行每行6个整数n,m,a,b,c,d. 1≤t≤20. 3≤n,m≤105,1≤c<a≤n,1≤b<d≤m. 输出 对于每组数据，输出对109+7取模之后的结果. 样例输入 2 3 3 3 1 1 3 10 7 8 4 3 5 样例输出 4 2975 提示 第一个样例解释 走在黑色区域是无效的。 来源 Ocean_Star_T
#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <utility> #include <vector> #include <map> #include <queue> #include <stack> #include <cstdlib> typedef long long ll; #define lowbit(x) (x&(-x)) #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 using namespace std; const ll mod=1e9+7; ll n,m,a,b,c,d; const int N=1e6+9;//大于2e5 ll mul(ll a,ll b){ a%=mod;b%=mod; return a*b%mod; } ll mul1(ll a,ll b,ll c){ a%=mod;b%=mod;c%=mod; return a*b%mod*c%mod; } ll fac[N]={1,1},inv[N]={1,1},f[N]={1,1}; void init() { for(int i=2;i<N;i++){ fac[i]=fac[i-1]*i%mod; f[i]=(mod-mod/i)*f[mod%i]%mod; inv[i]=inv[i-1]*f[i]%mod; } } ll C(ll a,ll b) { if(b>a) return 0; return fac[a]*inv[b]%mod*inv[a-b]%mod; } int main() { init(); int t; scanf("%d",&t); while(t--){ scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&a,&b,&c,&d); ll sum1=0,sum2=0;
// 上面两幅图加一起即可 for(int i=b+1;i<=d-1;i++){ ll x=C(c+i-2,c-1); ll y=C(n+m-c-i-1,n-c-1); ll z=mul(x,y); sum1=(sum1%mod+z)%mod; } for(int j=c+1;j<=a-1;j++){ ll x=C(j+b-2,b-1); ll y=C(n+m-b-j-1,m-b-1); ll z=mul(x,y); sum2=(sum2%mod+z)%mod; } ll sum=(sum1%mod+sum2%mod)%mod; printf("%lld\n",sum); } return 0; }
//The 2018 ACM-ICPC China JiangSu Provincial Programming Contest B Massage JSZKC feels so bored in the classroom that he wants to send massages to his girl friend. However, he can't move to his girl friend by himself. So he has to ask his classmates for help. The classroom is a table of size N \times MN×M. We'll consider the table rows numbered from top to bottom 11 through NN, and the columns numbered from left to right 11 through MM. Then we'll denote the cell in row xx and column yy as (x, y)(x,y). And every cell sits a student. Initially JSZKC sits on the cell (1, 1)(1,1) . And his girl friend sits on cell (n, m)(n,m). A message can go from cell (x, y)(x,y) to one of two cells (x + 1, y)(x+1,y) and (x, y + 1)(x,y+1). JSZKC doesn't want to trouble his classmates too much. So his classmates(not including his girl friend) may not take massages more than once. It's obvious that he can only send out two massages. Please help JSZKC find the number of ways in which the two massages can go from cell (1, 1)(1,1) to cell (n, m)(n,m). More formally, find the number of pairs of non-intersecting ways from cell (1, 1)(1,1) to cell (n, m)(n,m) modulo 10000000071000000007 . Two ways are called non-intersecting if they have exactly two common points — the starting point and the final point. Input Format The input file contains several test cases, each of them as described below. The first line of the input contains one integers NN (2 \le N,M \le 1000)(2≤N,M≤1000), giving the number of rows and columns in the classroom. There are no more than 100100 test cases. Output Format One line per case, an integer indicates the answer mod 10000000071000000007. 样例输入 复制 2 2 2 3 3 3 样例输出 复制 1 1 3 题目来源 The 2018 ACM-ICPC China JiangSu Provincial Programming Contest
1 (x1, y1) 到 (x2, y2) 的所有路径方案数：x = x2-x1, y = y2-y1, C(x+y, x) 就是方案数。 2 3 /* 4 A1(1,2) A2(2,1) 5 B1(n-1,m) B2(n,m-1) 6 并且只能从A1到B1,从A2到B2.组合数问题。 7 由容斥知：要再减去有交点的路线。 8 分析： 9 如果两条路线有交点，那么A1一定可以到B2，A2一定会到B1 10 */
1 ll n,m; 2 void egcd(ll a,ll b,ll &x,ll &y,ll &d) 3 { 4 if(!b) d=a,x=1,y=0; 5 else{ 6 egcd(b,a%b,y,x,d); 7 y-=x*(a/b); 8 } 9 } 10 ll inv(ll t){ 11 ll x,y,d; 12 egcd(t,mod,x,y,d); 13 return d==1?(x%mod+mod)%mod:-1; 14 } 15 ll C(ll n,ll m){ 16 if(n<m) return 0; 17 ll ans=1; 18 for(int i=1;i<=m;i++){ 19 ans=(ans*(n-m+i)%mod*inv(i)%mod)%mod; 20 } 21 return ans%mod; 22 } 23 ll mul(ll a,ll b){ 24 a%=mod,b%mod; 25 return a*b%mod; 26 } 27 ll mull(ll a,ll b,ll c) 28 { 29 a%=mod,b%=mod,c%=mod; 30 return a*b%mod*c%mod; 31 } 32 int main() 33 { 34 while(~scanf("%lld%lld",&n,&m)){ 35 ll ans1=C(n+m-4,n-2); 36 ll ans2=C(n+m-4,n-1); 37 ll ans3=C(n+m-4,m-1);//不能用n-3，因为n-3可能为负数，那么结果就是1了。 38 ll ans4=(mul(ans1,ans1)-mul(ans2,ans3)+mod)%mod; 39 printf("%lld\n",ans4); 40 } 41 return 0; 42 }
