JAVA 图论
拓扑排序
210. 课程表 II
难度中等
现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。
- 例如，想要学习课程
0，你需要先完成课程1，我们用一个匹配来表示：[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。
基于BFS实现 只能输出一种
class Solution { List<List<Integer>>edge = new ArrayList<List<Integer>>(); int res[]; int in[]; public int[] findOrder(int numCourses, int[][] prerequisites) { res =new int[numCourses]; in =new int[numCourses]; for(int i=0;i<numCourses;i++) edge.add(new ArrayList<Integer>()); for(int a[]:prerequisites) { edge.get(a[1]).add(a[0]); in[a[0]]++; } Queue<Integer>que = new LinkedList(); for(int i=0;i<numCourses;i++){ if(in[i]==0) que.offer(i); } int id =0; while(!que.isEmpty()){ int tmp = que.poll(); res[id++] =tmp; for(int z:edge.get(tmp)){ in[z]--; if(in[z]==0) que.offer(z); } } if(id!=numCourses) return new int[0];//有环 return res; } }
N个节点，M条边
时空复杂度都为O（M+N）
针对上述代码进行离散化 int a_[] = new int[a.length]; Arrays.sort(a); for (int i = 0; i < a.length; i++) { a_[i] = Arrays.binarySearch(a, a[i]); map.put(a[i], a_[i]); } int po[][] = { { 3, 1 }, { 4, 3 }, { 5, 4 }, { 2, 4 } }; int po_[][] = new int[po.length][po[0].length]; int i = 0; for (int x[] : po) { po_[i][0] = map.get(x[0]); po_[i][1] = map.get(x[1]); i++; }
DFS 输出所有拓扑排序
import java.util.*; import javax.annotation.processing.SupportedOptions; public class Main { static List<List<Integer>> edge = new ArrayList<List<Integer>>(); static int res[]; static Map<Integer, Integer> map = new HashMap<>(); static boolean vis[], viss[][]; static int n, ans = 0; static int a[] = { 1, 2, 3, 4, 5 }; static int a_[]; public static boolean ok(int i, int cnt) { for (int j = 0; j < cnt; j++) { if (viss[i][res[j]]) return false; } return true; } public static void dfs(int cnt) {//第cnt个数 if (cnt == n) { ans++; for (int i = 0; i < cnt; i++) { System.out.print(res[i] + " "); } System.out.println(" "); return; } for (int j = 0; j < n; j++) { if (!vis[a_[j]] && ok(a_[j], cnt)) { vis[a_[j]] = true; res[cnt] = a_[j]; dfs(cnt + 1); vis[a_[j]] = false; } // if (!vis[a_[j]]) { // vis[a_[j]] = true; // res[cnt] = a_[j]; // dfs(cnt + 1); // vis[a_[j]] = false; // } } } public static void main(String[] args) { n = a.length; // 离散化 [0,n-1] a_ = new int[n]; res = new int[n]; Arrays.sort(a); for (int i = 0; i < n; i++) { a_[i] = Arrays.binarySearch(a, a[i]); map.put(a[i], a_[i]); } vis = new boolean[n + 1]; viss = new boolean[n + 1][n + 1]; int po[][] = { { 3, 1 }, { 4, 3 }, { 5, 4 }, { 2, 4 } }; int po_[][] = new int[po.length][po[0].length]; int i = 0; for (int x[] : po) { po_[i][0] = map.get(x[0]); po_[i][1] = map.get(x[1]); viss[po_[i][1]][po_[i][0]] = true; i++; } dfs(0); } }
2127. 参加会议的最多员工数
难度困难
一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子，可以坐下 任意数目 的员工。
员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工 不会 是他自己。
给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。
按照题意，多个人围成一个环，环外可能枝连其他节点
（1）环内只有2个节点
1 和2坐在一起，5只能在2的右边，3，4，6只能在1的左边。3，4不能同时出现
这种情况，1为根的最长链+2为根的最长链
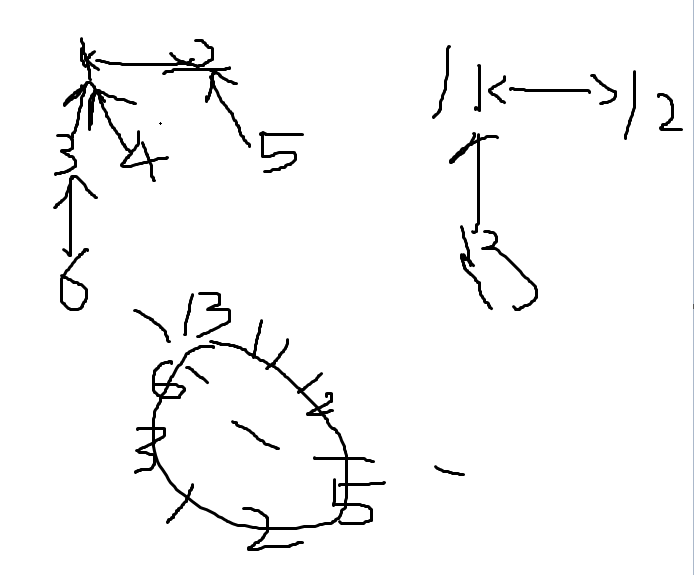
（2）环内有大于等于3个节点
7 8 9 围成一个环，10不能加入环，因为加入10会破坏原来的结构
第一种情况，可以并接。第二种情况，只能取一个环 因为只有一个桌子
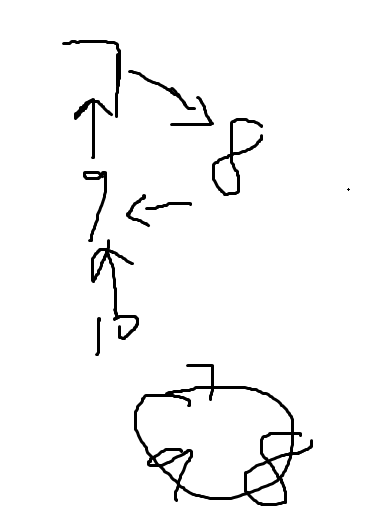
结果为（1）（2）的最大值
class Solution { public int maximumInvitations(int[] favorite) { int n =favorite.length; int f[] =new int[n+1]; int in[] =new int [n+1]; int u,v,cnt; for(int x:favorite){ in[x]++; } Arrays.fill(f,1); Queue<Integer>que =new LinkedList(); for(int i =0;i<n;i++) { if(in[i]==0) que.offer(i); } //去树枝 while(!que.isEmpty()){ u =que.poll(); v =favorite[u]; f[v] =Math.max(f[v],f[u]+1);//f[v]：v为根的最长链长度 in[v]--; if(in[v]==0) que.offer(v); } int two=0,three=0; for(int j=0;j<n;j++){ if(in[j]==1){ in[j]--; u =favorite[j]; if(favorite[u]==j){//2个点的环 two+=(f[j]+f[u]); in[u]--; } else{//大于等于3个点的环 cnt =1; while(u!=j){ cnt++; in[u]--; u = favorite[u]; } three =Math.max(three,cnt); } } } return Math.max(three,two); } }
