JAVA 位运算
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
位运算模拟加法
参考链接:https://blog.csdn.net/weixin_41521306/article/details/98784642?spm=1001.2101.3001.6650.3&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-3.pc_relevant_default&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-3.pc_relevant_default&utm_relevant_index=6
class Solution { public int add(int a, int b) { while(b!=0){ int tmp =a^b; //不进位运算结果 b =(a&b)<<1;//&找出需要进位的位,左移表示进位 a =tmp; } return a; } }
移位
int a = Integer.MIN_VALUE; System.out.println(a);//-2147483648 a = Math.abs(a); System.out.println(a);// -2147483648 int x = -16; String s = Integer.toBinaryString(x); System.out.println(x + " " + s); int y = x >> 2; String ss = Integer.toBinaryString(y); System.out.println(y + " " + ss); int z = x >>> 2; String sss = Integer.toBinaryString(z); System.out.println(z + " " + sss); // -16 // 1111 1111 1111 1111 1111 1111 1111 0000 // -16>>>2 :1073741820 // 11 1111 1111 1111 1111 1111 1111 1100 不考虑符号位 // -16>>2 :-4 // 1111 1111 1111 1111 1111 1111 1111 1100
JAVA int 范围
Java中int 占 4 个字节,一个字节为 8 bit,一个bit 为一个二进制01单位,所以int 为 32 bit
由于计算机存储数字时,第一位会被存储为符号位,所以当 int 为正数时,最大存储为:
0111 1111 1111 1111 1111 1111 1111 1111
十进制为:2147483647
最小存储为:
1111 1111 1111 1111 1111 1111 1111 1111 (原码)
1000 0000 0000 0000 0000 0000 0000 0000 (反码)
1000 0000 0000 0000 0000 0000 0000 0001 (补码)
补码转换为十进制数为:-2147483647
但是!!
在二进制中,0的表示有两种,分别为+0 和 - 0;在32位中表示为
+0 : 0000 0000 0000 0000 0000 0000 0000 0000
-0 : 1000 0000 0000 0000 0000 0000 0000 0000
因为0只有一个,便将 -0 拿来做最小的数,十进制为-2147483648
Integer.MAX_VALUE
Integer.MIN_VALUE
1 << 31 ~ (1 << 31) - 1;
Java:二进制(原码、反码、补码)与位运算
二进制的最高位是符号位(“0”代表正数,“1”代表负数);
Java中没有无符号数;
计算机以整数的补码进行运算;
1. 原码:将一个整数转换成二进制表示
以 int 类型为例,int类型占4个字节、共32位。
例如,2 的原码为:00000000 00000000 00000000 00000010
-2的原码为:10000000 00000000 00000000 00000010
2. 反码
正数的反码:与原码相同
负数的反码:原码的符号位不变,其他位取反
例如,-2 的反码为:11111111 11111111 11111111 11111101
3. 补码
正数的补码:与原码相同
负数的补码:反码+1
例如,-2 的补码为:01111111 11111111 11111111 11111110
总结
正数的原码、反码、补码都一样;
负数的反码 = 原码的符号位不变,其他位取反;
负数的补码 = 反码+1;
0的原码、反码、补码都是0;
计算机以补码进行运算;
取反不同于反码
剑指 Offer II 001. 整数除法
给定两个整数 a 和 b ,求它们的除法的商 a/b ,要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。
注意:
- 整数除法的结果应当截去(
truncate)其小数部分,例如:truncate(8.345) = 8以及truncate(-2.7335) = -2 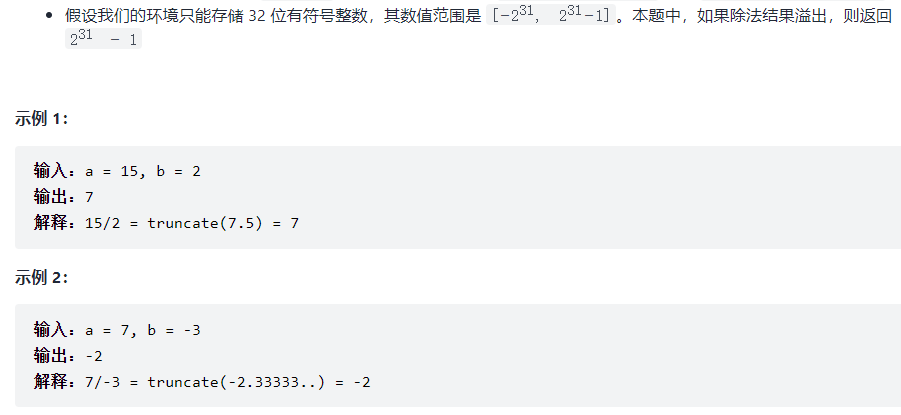

class Solution { public int divide(int a, int b) { if(a==Integer.MIN_VALUE&&b==-1) return Integer.MAX_VALUE; //溢出 int sign =(a>0)^(b>0)?-1:1; //-2^31转换为2^31会溢出,所以全部转换为负数 if(a>0) a=-a; if(b>0)b=-b; int ans =0; while(a<=b){ a-=b; ans++; } return sign==1?ans:-ans; } }

-
class Solution { public int divide(int a, int b) { if(a==Integer.MIN_VALUE&&b==-1) return Integer.MAX_VALUE; //溢出 int sign =(a>0)^(b>0)?-1:1; //-2^31转换为2^31会溢出,所以全部转换为负数 if(a>0) a=-a; if(b>0)b=-b; int ans =0; int tmp = (int) ((-1) * Math.pow(2, 30)); while(a<=b){ int val = b; int k=1; while(val>=tmp&&a<=val*2){//val>=tmp 不然val<<=1(-2^31)溢出 val<<=1; k<<=1; } a-=val; ans+=k; } a =-22,b=-3 >>>>>>>>>>>>>>>>> val=-3,k=1 val=-3*2=-6,k=1+1=2 val=-3*2*2=-12,k=2+2=4 val=-3*2*2=-24,a>val a=a-val=-22-(-12)=-10,ans=0+4=4 >>>>>>>>>>>>>>>>>> val=-3,k=1 val=-3*2=-6,k=1+1=2 val=-3*2*2=-12,a=-10>-12 a=a-val=-10-(-6)=-4,ans=4+2=6 >>>>>>>>>>>>>>>>>> val=-3,k=1 val=-3*2=-6,a>val a=a-val=-4-(-6)=2,ans=6+1=7 a=2>b=-3 时间复杂度;logn*logn return 7 return sign==1?ans:-ans; } }

class Solution { public int divide(int a, int b) { if(a==Integer.MIN_VALUE&&b==-1) return Integer.MAX_VALUE; //溢出 int sign =(a>0)^(b>0)?-1:1; a =Math.abs(a);b=Math.abs(b); int ans =0; for(int i=31;i>=0;i--){ //>>> 无符号右移,-2^31 会被转换为2^31 if((a>>>i)-b>=0){//(a>>>i)>=b 错的,因为如果b=-2^31会一直true a-=(b<<i); ans+=(1<<i); } } return sign==1?ans:-ans; } }
-






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 一文读懂知识蒸馏
· 终于写完轮子一部分:tcp代理 了,记录一下
2020-01-15 第六周 第三部分