数据的分析----分析检验
分析---描述统计-----频率
频率：统计 百分位值 四分位数 （如100个数中，第25 50 75 100个参数是多少）
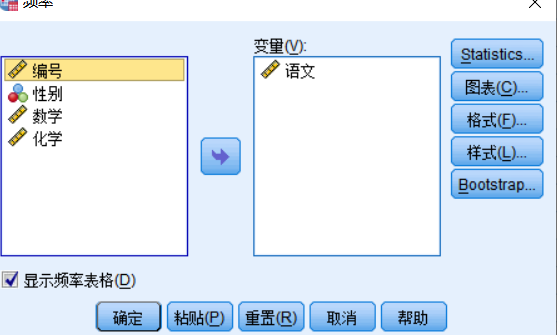
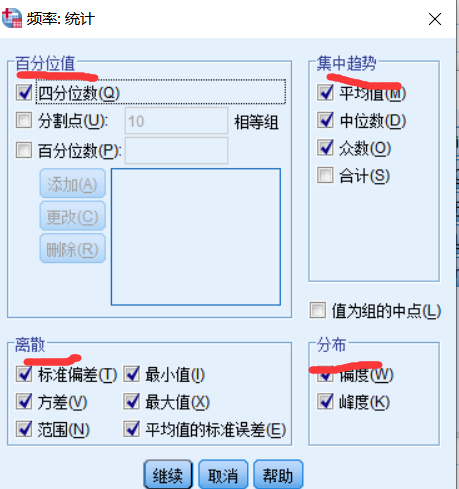
值为组的中点：如【30，40】内的值全部编码为35，那么选择此选项以估计原始未分组的数据的中位数和百分位数。
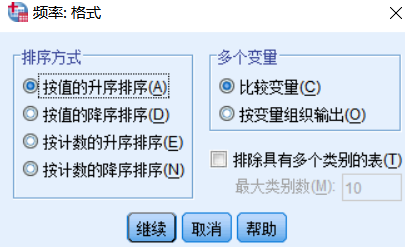
多个变量：比较变量就是指多个变量的频数表集中输出。按变量组织输出：每个变量单独输出。
偏度(skewness)和峰度(kurtosis）
- 偏度（Skewness）
- 定义
偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性的特征统计量。
公式
定义上偏度是样本的标准三阶中心矩（standardized 3rd central moment)。
偏度的具体计算公式为：
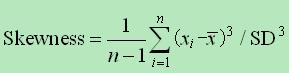
性质
这个统计量同样需要与正态分布相比较，
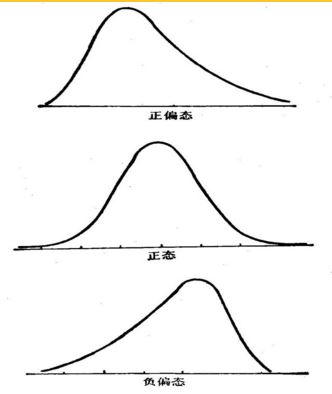
偏度 =0表示其数据分布形态与正态分布的偏斜程度相同；
偏度 >0表示其数据分布形态与正态分布相比为正偏（右偏），即有一条长尾巴拖在右边，数据右端有较多的极端值，数据均值右侧的离散程度强；
偏度 <0表示其数据分布形态与正态分布相比为负偏（左偏），即有一条长尾拖在左边，数据左端有较多的极端值，数据均值左侧的离散程度强
偏度的绝对值数值越大表示其分布形态的偏斜程度越大。
当偏度值超过标准误差2倍时认为分布不对称
- 峰度（Kurtosis）
- 定义
峰度又称峰态系数，表征概率密度分布曲线在平均值处峰值高低的特征数，即是描述总体中所有取值分布形态陡缓程度的统计量。直观看来，峰度反映了峰部的尖度。这个统计量需要与正态分布相比较。
公式
定义上峰度是样本的标准四阶中心矩（standardized 4rd central moment)。
随机变量的峰度计算方法为随机变量的四阶中心矩与方差平方的比值。
具体计算公式为：
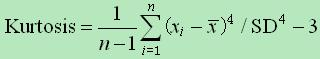
性质
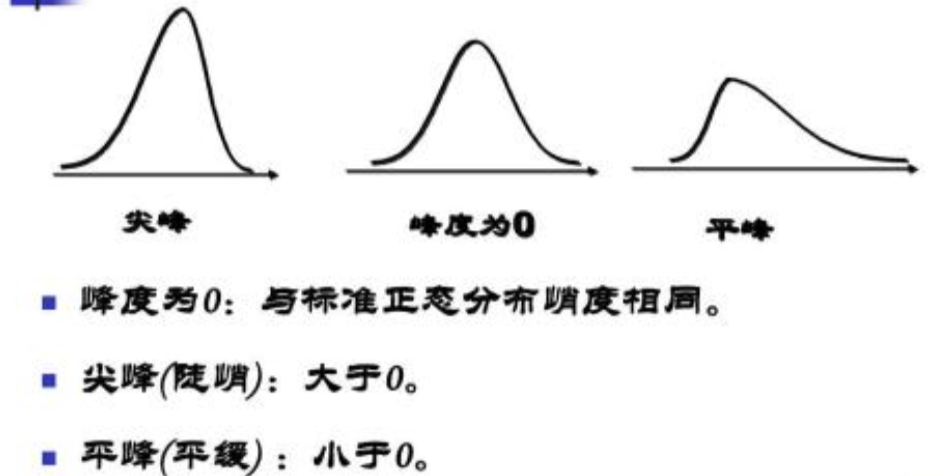
峰度 =0表示该总体数据分布与正态分布的陡缓程度相同；
峰度 >0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；
峰度 <0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
描述性统计分析
分析--描述统计----描述
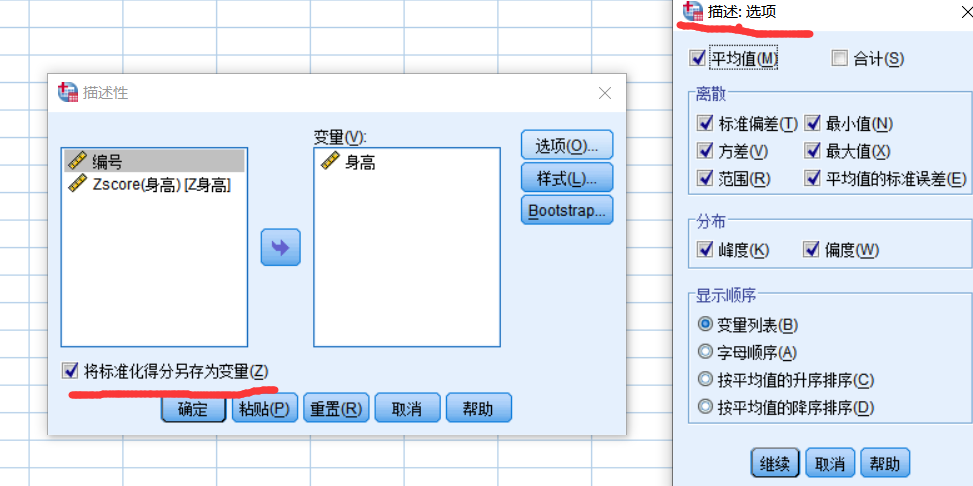
标准化：（数据-均值）/标准差
探索性分析
分析---描述统计---探索
使用探索过程的原因：数据过滤，离群值识别、描述、假设检验以及描述子群体之间差异的特征
因变量：你要研究的变量 ，因子列表表示分类
界外值：会输出5个最大值和最小值
百分位数： 第5 10 25 50 75 90 95百分位的值
图
箱图 ：当您具有一个或多个因变量时，这些选项控制箱图的显示。
大于箱子高度（75%：第三四分位数-25：第一四分位数）1.5 ~3倍称为离群值，大于箱子高度3倍以上的值称为极值
- 按因子级别分组
- 为每个因变量生成单独的显示。在一个显示中，将为因子变量定义的每个组显示箱图。
- 不分组
- 为因子变量所定义的每个组生成单独的显示。在一个显示中，为每个因变量并排显示箱图。当不同的变量代表在不同的时间度量的同一个特征时，此显示尤其有用。
- 无
- 不会为因变量或组生成单独的显示
- 带检验的正态图：对数据进行概率分布检验，显示正态的概率分布图和离散的正态的概率分布图
-
M估计值是什么？
选择M-estimation复选项，求出集中趋势的稳健估计，该统计量是利用迭代方法计算出来，一般来说受异常值影响要小的多。
如果该统计量离均数和中位数较远，则说明数据中可能存在异常值，此时宜用该估计值替代均数以反映集中趋势。
一共会输出Huber、Andrew、Hampel和Tukey四种M统计量，其中Huber法适用于数据接近正态分布的情况，另三种则适用于数据中有许多异常值时；
正态概率图来用于检查一组数据是否服从正态分布。是实数与正态分布数据之间函数关系的
散点图。如果这源组实数服从正态分布，正态概率图将是一条直线，变量值越接近斜线，说明变量值越接近正态分布。通常以用于确定一组数据是否百服从任一已知分布，如二项分布或泊松分度布。反趋势正态Q-Q图，
常态性检验：显著性<0.05 ,说明不符合正态分布，存在一些异常值。
伸展与级别levene检验:当选入分组变量时，该功能才被激活，主要用于比较各组之间的离散程度是否一致。在这里可以选择“未转换”，用于方差齐性检
（方差齐性检验：显著性<0.05，不齐性。分析-描述统计-探索-绘制)
控制分布-水平图的数据转换。对于所有分布-水平图，显示回归线的斜率和Levene 的稳健的方差齐性检验。如果选择转换，则Levene 检验基于转换后的数据。如果未选择因子变量，则不生成分布-水平图。
◎幂估计（求最佳的幂转换值，为已转换做铺垫）针对所有单元的中位数的自然对数以及幂转换的估计值生成内距的自然对数图，以在各单元中得到相等的方差。分布-水平图协助确定稳定（使之更相等）组之间方差所需的转换的幂。
◎使用已变换可以选择幂替代值之一（可能按幂估计中的推荐），并生成转换数据图。绘制转换数据的内距和中位数。
◎未变换生成原始数据的图。这等于幂为1 的转换。无是不进行检验，未转换是用原始数据进行检验
缺失值控制对缺失值的处理。
- 成列排除个案
- 从所有分析中排除任何因变量或因子变量具有缺失值的个案。这是缺省值。
- 成对排除个案
- 在该组的分析中包含组（单元格）中变量不具有缺失值的个案。该个案可能在其他组中使用的变量中有缺失值。
