CNN中的卷积

1、什么是卷积：图像中不同数据窗口的数据和卷积核（一个滤波矩阵）作内积的操作叫做卷积。其计算过程又称为滤波（filter)，本质是提取图像不同频段的特征。

2、什么是卷积核：也称为滤波器filter，带着一组固定权重的神经元，通常是n*m二维的矩阵，n和m也是神经元的感受野。n*m 矩阵中存的是对感受野中数据处理的系数。一个卷积核的滤波可以用来提取特定的特征（例如可以提取物体轮廓、颜色深浅等）。通过卷积层从原始数据中提取出新的特征的过程又成为feature map(特征映射)。filter_size是指filter的大小，例如3*3； filter_num是指每种filter_size的filter个数，通常是通道个数

3、什么是卷积层：多个滤波器叠加便成了卷积层。

4、一个卷基层有多少个参数：一个卷积核使用一套权值以便”扫视’数据每一处时以同样的方式抽取特征，最终得到的是一种特征。在tensorflow定义conv2d时需要指定卷积核的尺寸，本人现在的理解是一个卷积层的多个卷积核使用相同的m*n, 只是权重不同。则一个卷积层的参数总共m*n*filter_num个，比全连接少了很多。

5、通道(chennel）怎么理解：通道可以理解为视角、角度。例如同样是提取边界特征的卷积核，可以按照R、G、B三种元素的角度提取边界，RGB在边界这个角度上有不同的表达；再比如需要检查一个人的机器学习能力，可以从特征工程、模型选择、参数调优等多个方面检测

tf.Variable()用于生成一个初始值为initial-value的变量；必须指定初始化值。

tf.Variable trainable的作用

input_data = tf.Variable(data_initalizer, trainable=False, collections=[])
设定trainable=False 可以防止该变量被数据流图的 GraphKeys.TRAINABLE_VARIABLES 收集,
这样我们就不会在训练的时候尝试更新它的值。

tf.get_variable()获取已存在的变量(要求不仅名字，而且初始化方法等各个参数都一样)，如果不存在，就新建一个；可以用各种初始化方法，不用明确指定值。

# 使用正态分布初始化核
kernel = tf.get_variable(name + "W", [k_size, k_size, nums_in, nums_out],
                         initializer=tf.truncated_normal_initializer(stddev=0.01))

tf.get_variable函数的使用

tf.get_variable(name, shape, initializer): name就是变量的名称，shape是变量的维度，initializer是变量初始化的方式，初始化的方式有以下几种：

tf.constant_initializer：常量初始化函数

tf.random_normal_initializer：正态分布

tf.truncated_normal_initializer：截取的正态分布

tf.random_uniform_initializer：均匀分布

tf.zeros_initializer：全部是0

tf.ones_initializer：全是1

tf.uniform_unit_scaling_initializer：满足均匀分布，但不影响输出数量级的随机值

import tensorflow as tf

t = tf.truncated_normal_initializer(stddev=0.1, seed=1)
v = tf.get_variable('v', [1], initializer=t)

with tf.Session() as sess:
    for i in range(1, 10, 1):
        sess.run(tf.global_variables_initializer())
        print(sess.run(v))

[-0.08113182]
[0.06396971]
[0.13587774]
[0.05517125]
[-0.02088852]
[-0.03633211]
[-0.06759059]
[-0.14034753]
[-0.16338211]

tf.truncated_normal_initializer 从截断的正态分布中输出随机值。
生成的值服从具有指定平均值和标准偏差的正态分布，如果生成的值大于平均值2个标准偏差的值则丢弃重新选择。

ARGS：

mean：一个python标量或一个标量张量。要生成的随机值的均值。
stddev：一个python标量或一个标量张量。要生成的随机值的标准偏差。
seed：一个Python整数。用于创建随机种子。查看 tf.set_random_seed 行为。
dtype：数据类型。只支持浮点类型

在tf.truncated_normal中如果x的取值在区间（μ-2σ，μ+2σ）之外则重新进行选择。这样保证了生成的值都在均值附近。

tf.global_variables_initializer()什么时候用？

import tensorflow as tf
# 必须要使用global_variables_initializer的场合
# 含有tf.Variable的环境下，因为tf中建立的变量是没有初始化的，也就是在debug时还不是一个tensor量，而是一个Variable变量类型
size_out = 10
tensor = tf.Variable(tf.random_normal(shape=[size_out]))
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init) # initialization variables
print(sess.run(tensor))
# 可以不适用初始化的场合
# 不含有tf.Variable、tf.get_Variable的环境下
# 比如只有tf.random_normal或tf.constant等
size_out = 10
tensor = tf.random_normal(shape=[size_out]) # 这里debug是一个tensor量哦
init = tf.global_variables_initializer()
with tf.Session() as sess:
# sess.run(init) # initialization variables
print(sess.run(tensor))

tf.pad()

tf.pad：填充函数

tf.pad( tensor,paddings, mode='CONSTANT',name=None)
1
tensor是要填充的张量
padings ，代表每一维填充多少行/列，它的维度一定要和tensor的维度是一样的，这里的维度不是传统上数学维度，如[[2,3,4],[4,5,6]]是一个3乘4的矩阵，但它依然是二维的，所以pad只能是[[1,2],[1,2]]这种。

mode 可以取三个值，分别是"CONSTANT" ,“REFLECT”,“SYMMETRIC”

mode=“CONSTANT” 填充0

mode="REFLECT"映射填充，上下（1维）填充顺序和paddings是相反的，左右（零维）顺序补齐

mode="SYMMETRIC"对称填充，上下（1维）填充顺序是和paddings相同的，左右（零维）对称补齐

t=[[2,3,4],[5,6,7]]
print（tf.pad(t,[[1,1],[2,2]],"CONSTANT"))）
输出

 [[0, 0, 0, 0, 0, 0, 0],
 [0, 0, 2, 3, 4, 0, 0],
 [0, 0, 5, 6, 7, 0, 0],
 [0, 0, 0, 0, 0, 0, 0]]

注：[1，1]是在pad里是第一个，代表第一维即矩阵的行，左边的1代表上方放一行0，右边的1代表下方放一行0
同理，2，2顺序是第二个，代表对列操作，左边的2代表在左边放两列0，右边2代表在右边放两列0

2.

 t=[[2,3,4],[5,6,7]]
    print（tf.pad(t,[[1,2],[2,3]],"CONSTANT"))）

输出

  [[0, 0, 0, 0, 0, 0, 0, 0],
  [0, 0, 2, 3, 4, 0, 0, 0],
  [0, 0, 5, 6, 7, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0, 0]]

1，2代表上方一行0，下方2行0；2，3代表列坐标放2列0，右边放3列0


  t=[[2,3,4],[5,6,7]]
        print（tf.pad(t,[[1,1],[2,2]],"REFLECT"))）

输出

[[7, 6, 5, 6, 7, 6, 5],
[4, 3, 2, 3, 4, 3, 2],
[7, 6, 5, 6, 7, 6, 5],
[4, 3, 2, 3, 4, 3, 2]]
行上方复制和行下方和对应位置复制相反，列左边和列右边以原第一列和原第三列维中轴复制



t=[[2,3,4],[5,6,7]]
    print（tf.pad(t,[[1,1],[2,2]],"SYMMETRIC"))）

输出：

  [[3, 2, 2, 3, 4, 4, 3],
   [3, 2, 2, 3, 4, 4, 3],
   [6, 5, 5, 6, 7, 7, 6],
   [6, 5, 5, 6, 7, 7, 6]]

对于三维矩阵你可以理解为那是一幢楼，三维矩阵的由二维矩阵构成，每个二维矩阵相当于一个楼层。
1. 对于三维矩阵的pad，就是在顶楼，底楼，每层楼的上，下，左，右补0

#pad1 = np.array([[‘顶’，‘底’],[‘上’，‘下’], [‘左’,‘右’ ]])

import numpy as np
import tensorflow as tf

tsr = tf.Variable(tf.ones([2, 3, 4]), name="tsr")
pad_top = np.array([[1, 0], [0, 0], [0, 0]])

pad_left = np.array([[0, 0], [0, 0], [3, 0]])


pad_up= np.array([[0, 0], [1, 0], [3, 0]])
tsr_pad_top = tf.pad(tsr, pad_top, name='pad_top')

tsr_pad_left = tf.pad(tsr, pad_left, name='pad_left')


tsr_pad_up = tf.pad(tsr, pad_up, name='pad_up')
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    print('original tensor')
    print(sess.run(tsr))
    print(' pad top')
    print(sess.run(tsr_pad_top))
    print('pad left')
    print(sess.run(tsr_pad_left))
    print('pad_up')
    print(sess.run(tsr_pad_up))

original tensor
[[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]

[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
pad top
[[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]

[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]

[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
pad left
[[[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]]

[[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]]]
pad_up
[[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]]

[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]
[0. 0. 0. 1. 1. 1. 1.]]]

tf.pad(tensor,paddings)

tesor 是要填充的张量；paddings 也是一个张量，代表每一维填充多少行/列。

pad_mat = np.array([[0, 0], [pad_size, pad_size], [pad_size, pad_size], [0, 0]])
x_pad = tf.pad(x, pad_mat)

x 是一个四维张量（batchsize, width, height, channels)

本例tensor的rank=4，即4维向量tensor.shape=[b,h,w,c]，则padings=[a=[a1,a2],b=[b1,b2],c=[c1,c2],d=[d1,d2]]同样也是4维

填充后的行踪为[b+a1+a2,h+b1+b2,w+c1+c2,c+d1+d2](相应维度增加)

import tensorflow as tf

input = np.ones([1, 5, 5, 1])
print(input.shape)
kernel_size = 3
pad_begin = (kernel_size - 1) // 2
pad_end = kernel_size - 1 - pad_begin
inputs = tf.pad(input, [[0, 0], [pad_begin, pad_end], [pad_begin, pad_end], [0, 0]])
print(pad_begin)
print(pad_end)
print(inputs)
print(input)
with tf.Session() as sess:
    inputs = sess.run(inputs)
    print(inputs)

(1, 5, 5, 1)

1
1
Tensor("Pad:0", shape=(1, 7, 7, 1), dtype=float64)
[[[[1.]
[1.]
[1.]
[1.]
[1.]]

[[1.]
[1.]
[1.]
[1.]
[1.]]

[[1.]
[1.]
[1.]
[1.]
[1.]]]]

[[[[0.]
[0.]
[0.]
[0.]
[0.]
[0.]
[0.]]

[[0.]
[1.]
[1.]
[1.]
[1.]
[1.]
[0.]]

[[0.]
[0.]
[0.]
[0.]
[0.]
[0.]
[0.]]]]

卷积操作 tensorflow tf.nn.conv2d

卷积操作


tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)

data_format
可选参数，表示输入数据的格式，有两种分别为：“NHWC”和“NCHW”，默认格式为”NHWC“

“NHWC”输入数据的格式为为[batch, in_height, in_width, in_channels]
“NCHW”输入数据的格式为为[batch, in_channels， in_height, in_width]

use_cudnn_on_gpu
可选参数，表示是否使用GPU，默认为True，即有过有GPU，则默认使用GPU

input
一个4维的数据格式，即输入数据的格式，跟data_format相关。即如果输入数据格式为”NCHW“的情况下需要设置data_format参数。

filter
一个长度为4的一维列表，[height,width,in_channels, out_channels]，即filter的map大小，以及涉及到的输入特征图和输出特征图的个数。#in_channels和input的in_channels相等，也就是有多少filter(kernel)

strides
表示步长，是一个长为4的一维数组，跟data_format互相对应，表示在data_format每一维上的移动步长。例如输入格式默认格式”NHWC“，则strides的设置为[1,stride,stride,1]
对应[batch,in_height, in_width, in_channels]第一个表示在一个样本的特征图上的移动，第二三个是在filter在特征图上的移动的跨度，第四个表示在一个样本的一个通道上移动。

padding
表示填充方式，”SAME”表示采用填充的方式 ，”VALID”表示采用不填充的方式，即输出大小跟输入大小不一样，输出大小= （输入图片大小-filter大小)/步长+1

最终输出[batch,size,size,out_channels]#size 为输出图片大小

先定义几个参数

输入图片大小 W×W
Filter大小 F×F （相当于卷积核大小，也可看作滤波器大小，卷积也是一种滤波）
步长 S（stride)
padding的像素个数 P

于是我们可以得出

N = (W − F + 2P )/S+1

输出图片大小为 N×N

图片输入大小和输出大小的关系

tensorflow官网定义的padding如下：

tf.nn.moments()函数解析

tf.nn.moments()函数用于计算均值和方差。
# 用于在指定维度计算均值与方差
tf.nn.moments(
x,
axes,
shift=None, # pylint: disable=unused-argument
name=None,
keep_dims=False)

参数：

x：一个Tensor，可以理解为我们输出的数据，形如 [batchsize, height, width, kernels]。

axes：整数数组，用于指定计算均值和方差的轴。如果x是1-D向量且axes=[0] 那么该函数就是计算整个向量的均值与方差。

shift：未在当前实现中使用。

name：用于计算moment的操作范围的名称。

keep_dims：产生与输入具有相同维度的moment，通俗点说就是是否保持维度。

Two Tensor objects: mean and variance.
两个Tensor对象：mean和variance.

解释如下：

mean 就是均值
variance 就是方差

import tensorflow as tf

img = tf.Variable(tf.random_normal([3, 3]))#二维
axis = list(range(len(img.get_shape()) - 1))
mean, variance = tf.nn.moments(img, [1],keep_dims=True)
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print(sess.run(img))
    print(axis)
    resultMean = sess.run(mean)
    print('resultMean',resultMean)
    resultVar = sess.run(variance)
    print('resultVar',resultVar)
#[0]:列[1]:行

[[ 0.49775678 0.28713414 -0.48870713]
[-1.1327987 0.39820173 -1.14245 ]
[ 0.30145168 1.0506634 0.27895787]]
[0]
resultMean [[ 0.09872792]
[-0.6256823 ]
[ 0.543691 ]]
resultVar [[0.17993362]
[0.52418476]
[0.12859483]]

import tensorflow as tf

img = tf.Variable(tf.random_normal([3, 3]))
#print(len(img.get_shape()))#len((3,3))=2
#print(list(range(6)))#[0, 1, 2, 3, 4, 5]
#print(list(range(1)))#[0]




img = tf.Variable(tf.random_normal([3, 3]))

axis = list(range(len(img.get_shape()) - 1))
mean, variance = tf.nn.moments(img, axis,keep_dims=True)#默认False
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print(sess.run(img))
    print(axis)
    resultMean = sess.run(mean)
    print('resultMean',resultMean)
    resultVar = sess.run(variance)
    print('resultVar',resultVar)

[[-1.8180082 0.66420233 -0.02453276]
[ 0.48498765 -0.2215215 1.0879757 ]
[-0.40685716 1.0621067 1.0849667 ]]
[0]
resultMean [[-0.5799592 0.50159585 0.7161365 ]]
resultVar [[0.8989472 0.28783736 0.27429703]]

import tensorflow as tf

img = tf.Variable(tf.random_normal([128, 32, 32, 64]))
axis = list(range(len(img.get_shape()) - 1))
mean, variance = tf.nn.moments(img, axis)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# print(sess.run(img))
print(axis)
resultMean = sess.run(mean)
print('resultMean',resultMean)
resultVar = sess.run(variance)
print('resultVar',resultVar)

[0, 1, 2]
resultMean [ 1.2327734e-03 -5.7489763e-04 3.1536159e-03 -3.8074462e-03
1.0438575e-03 9.5636037e-04 -1.9286427e-03 2.5686688e-05
1.5976968e-03 4.2974550e-04 4.4996231e-03 -2.0782601e-03
-1.9817003e-03 -1.1562010e-03 4.1045356e-03 3.8733642e-04
2.4551406e-04 2.8959131e-03 3.9314087e-05 -5.2733213e-04
2.4218510e-03 1.5939489e-03 2.6208845e-03 -9.2810171e-04
-3.3988156e-03 4.7417381e-03 -6.4486562e-04 -2.4678649e-03
3.4471287e-03 -6.1192235e-04 4.0119025e-03 -3.4235092e-04
1.4669285e-04 -4.0030158e-03 -4.7141253e-03 -1.9648715e-03
1.1924999e-03 4.6375818e-03 -1.2788011e-03 -9.3602284e-05
2.2512849e-03 -7.5759791e-04 2.7626564e-04 -9.9496462e-04
-1.9146289e-03 7.2574452e-04 2.1744678e-03 8.7426364e-04
2.9862977e-03 1.8585455e-03 -1.2111352e-03 5.0664903e-04
-7.1739597e-04 -6.6187856e-04 2.5334922e-03 1.3100414e-03
-1.1279093e-03 1.9736639e-03 1.2486374e-03 9.3611993e-04
4.5500821e-03 -1.3877301e-03 -6.6459179e-04 3.1590315e-03]
resultVar [1.0024877 0.9982781 1.005957 0.992763 0.9985966 1.0018215
0.99724865 1.0054947 0.9939338 0.99986434 1.0018445 1.0029937
1.0016607 1.004672 0.9897978 0.9995274 1.0023481 0.9995155
0.99922705 1.0011554 0.9978574 0.99965453 0.9997068 1.0062482
1.0005778 0.9983364 1.0011382 1.0022066 1.0060494 0.9992455
1.0031801 1.0080976 0.99797106 1.0003812 1.0034088 0.9896556
0.9991884 1.0000468 0.99951273 1.0037884 0.9940268 0.99904686
0.996113 0.9923252 0.9966772 0.99976707 0.99650925 1.0044343
1.0023524 1.0064523 0.9965649 0.999834 0.9977493 1.0102488
0.9983424 0.9976944 0.999663 0.99214196 1.0037789 0.99998736
1.0040503 1.0005592 1.0068123 0.9973132 ]

形如[128, 32, 32, 64]的数据在CNN的中间层非常常见，为了给出一个直观的认识，函数的输出结果如下，可能输出的数字比较多。

> axis :[0, 1, 2]

对于 [128, 32, 32, 64] 这样的4维矩阵来说，一个batch里的128个图，经过一个64kernels卷积层处理，得到了128 * 64个图，再针对每一个kernel所对应的128个图，求它们所有像素的mean和variance，因为总共有64个kernels，输出的结果就是一个一维长度64的数组。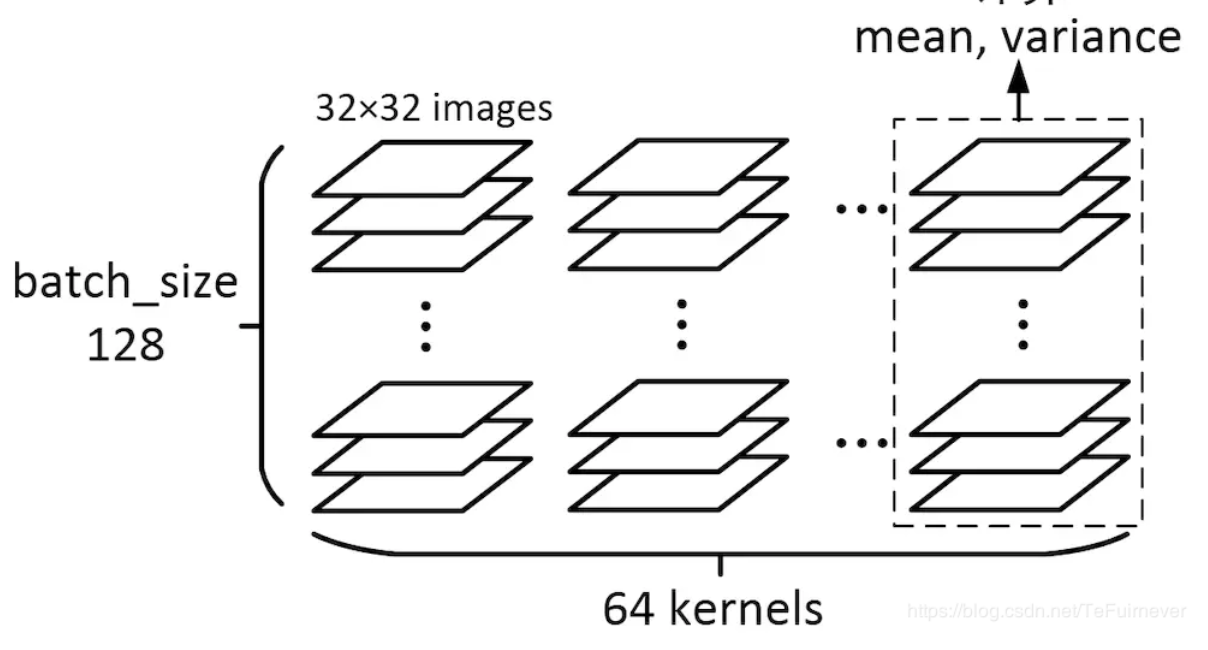

tf.matmul() 和tf.multiply() 的区别

import tensorflow as tf

a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3])
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2])
c = tf.matmul(a, b)
with tf.Session() as sess:
    print(sess.run([a, b, c]))

1.tf.multiply（）两个矩阵中对应元素各自相乘

格式: tf.multiply(x, y, name=None)
参数:
x: 一个类型为:half, float32, float64, uint8, int8, uint16, int16, int32, int64, complex64, complex128的张量。
y: 一个类型跟张量x相同的张量。
返回值： x * y element-wise.
注意：
（1）multiply这个函数实现的是元素级别的相乘，也就是两个相乘的数元素各自相乘，而不是矩阵乘法，注意和tf.matmul区别。
（2）两个相乘的数必须有相同的数据类型，不然就会报错。

2.tf.matmul（）将矩阵a乘以矩阵b，生成a * b。

格式: tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)
参数:
a: 一个类型为 float16, float32, float64, int32, complex64, complex128 且张量秩 > 1 的张量。
b: 一个类型跟张量a相同的张量。
transpose_a: 如果为真, a则在进行乘法计算前进行转置。
transpose_b: 如果为真, b则在进行乘法计算前进行转置。
adjoint_a: 如果为真, a则在进行乘法计算前进行共轭和转置。
adjoint_b: 如果为真, b则在进行乘法计算前进行共轭和转置。
a_is_sparse: 如果为真, a会被处理为稀疏矩阵。
b_is_sparse: 如果为真, b会被处理为稀疏矩阵。
name: 操作的名字（可选参数）
返回值：一个跟张量a和张量b类型一样的张量且最内部矩阵是a和b中的相应矩阵的乘积。
注意：
（1）输入必须是矩阵（或者是张量秩 >２的张量，表示成批的矩阵），并且其在转置之后有相匹配的矩阵尺寸。
（2）两个矩阵必须都是同样的类型，支持的类型如下：float16, float32, float64, int32, complex64, complex128。
引发错误:
ValueError: 如果transpose_a 和 adjoint_a, 或 transpose_b 和 adjoint_b 都被设置为真

import tensorflow as tf

a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3])
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2])
c = tf.matmul(a, b)
with tf.Session() as sess:
    print(sess.run(c))

[[ 58 64]
[139 154]]

c = tf.multiply(a, b)
with tf.Session() as sess:
    print(sess.run(c))

[[ 7 16 27]
[40 55 72]]

posted on 2020-03-22 23:40 cltt 阅读(493) 评论(0) 编辑收藏举报

刷新页面返回顶部