Batch normalization和Instance normalization的对比
原文链接: https://www.zhihu.com/question/68730628/answer/607608890
BN和IN其实本质上是同一个东西,只是IN是作用于单张图片,但是BN作用于一个batch。
一.BN和IN的对比
假如现有6张图片x1,x2,x3,x4,x5,x6,每张图片在CNN的某一卷积层有6个通道,也就是6个feature map。有关Batch Normalization与Instance Normalization的区别请看下图:
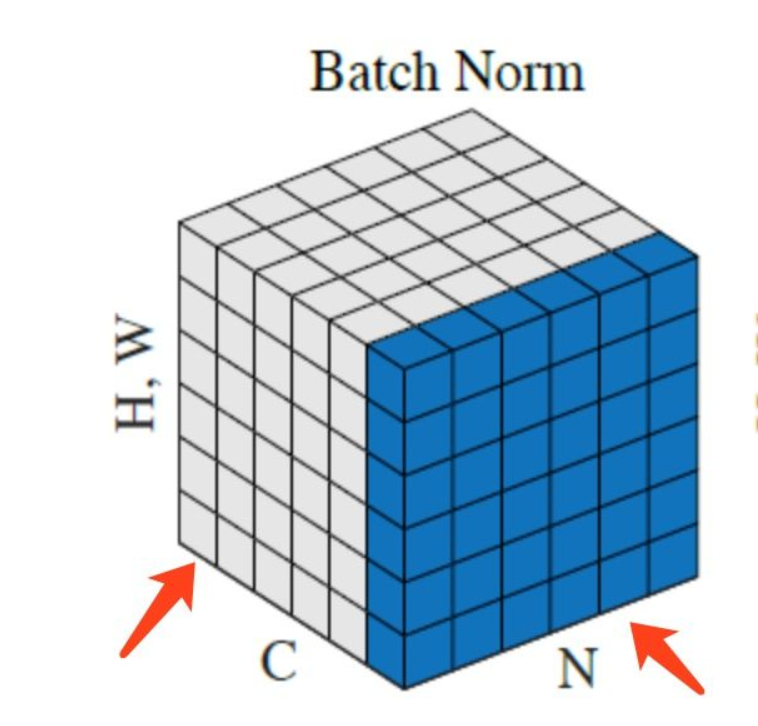

上图中,从C方向看过去是指一个个通道,从N看过去是一张张图片。每6个竖着排列的小正方体组成的长方体代表一张图片的一个feature map。蓝色的方块是一起进行Normalization的部分。
由此就可以很清楚的看出,Batch Normalization是指6张图片中的每一张图片的同一个通道一起进行Normalization操作。而Instance Normalization是指单张图片的单个通道单独进行Noramlization操作。
二.各自适用场景
BN适用于判别模型中,比如图片分类模型。因为BN注重对每个batch进行归一化,从而保证数据分布的一致性,而判别模型的结果正是取决于数据整体分布。但是BN对batchsize的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布;
IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,在风格迁移中使用Instance Normalization不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立。


四.算法的过程
4.1 BN
- 沿着通道计算每个batch的均值u
- 沿着通道计算每个batch的方差σ^2
- 对x做归一化,x’=(x-u)/开根号(σ^2+ε)
- 加入缩放和平移变量γ和β ,归一化后的值,y=γx’+β
4.2 IN
- 沿着通道计算每张图的均值u
- 沿着通道计算每张图的方差σ^2
- 对x做归一化,x’=(x-u)/开根号(σ^2+ε)
- 加入缩放和平移变量γ和β ,归一化后的值,y=γx’+β
算法的作用
BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。 BN算法在网络中的作用 BN算法像卷积层,池化层、激活层一样也输入一层。BN层添加在激活函数前,对输入激活函数的输入进行归一化。这样解决了输入数据发生偏移和增大的影响。 优点: 1、加快训练速度,能够增大学习率,即使小的学习率也能够有快速的学习速率; 2、不用理会拟合中的droupout、L2 正则化项的参数选择,采用BN算法可以省去这两项或者只需要小的L2正则化约束。
原因,BN算法后,参数进行了归一化,原本经过激活函数没有太大影响的神经元,分布变得明显,经过一个激活函数以后,神经元会自动削弱或者去除一些神经元,就不用再对其进行dropout。
另外就是L2正则化,由于每次训练都进行了归一化,就很少发生由于数据分布不同导致的参数变动过大,带来的参数不断增大。 3、 可以把训练数据集打乱,防止训练发生偏移。
x:input
mean:样本均值
variance:样本方差
offset:样本偏移(相加一个转化值)
scale:缩放(默认为1)
variance_epsilon:为了避免分母为0,添加的一个极小值
class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)[source] 对小批量(mini-batch)3d数据组成的4d输入进行批标准化(Batch Normalization)操作
在每一个小批量(mini-batch)数据中,计算输入各个维度的均值和标准差(多张图片的同一通道一起考虑)。gamma与beta是可学习的大小为C的参数向量(C为输入通道数) 在训练时,该层计算每次输入的均值与方差,并进行移动平均。移动平均默认的动量值为0.1。 在验证时,训练求得的均值/方差将用于标准化验证数据。 参数: num_features: 来自期望输入的特征数,该期望输入的大小为'batch_size x num_features x height x width' eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。 momentum: 动态均值和动态方差所使用的动量。默认为0.1。 affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数。 Shape: - 输入:(N, C,H, W) - 输出:(N, C, H, W)(输入输出相同)
在使用pytorch的 nn.BatchNorm2d() 层的时候,经常地使用方式为在参数里面只加上待处理的数据的通道数(out_channel,特征数量),但是有时候会在后面再加入一个小数,比如这样 nn.BatchNorm2d(64,0.8),这里面的0.8有什么作用呢? 我们知道在训练过程中 nn.BatchNorm2d() 的作用是根据统计的mean 和var来对数据进行标准化,并且这个mena和var在每个batch中都会进行,为了使得数据更有统计意义,
使得整个训练数据的特征都能够被保存,则在每个batch过程中,都会对网络的mean和var进行更新,这里就涉及到新的 batch的统计数据mean和var与网络已经保存的这两个统计数据之间的取舍问题了,而这个0.8就指定了保存的比例,
这个参数名为momentum.
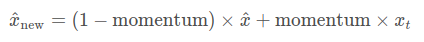
参数更新是以差分的形式进行的,xt代表新一轮batch产生的数据,x^代表历史数据,这个参数越大,代表当前batch产生的统计数据的重要性越强。
pytorch方法测试详解——归一化(BatchNorm2d)
import torch import torch.nn as nn m = nn.BatchNorm2d(2,affine=True) #权重w和偏重将被使用学习 input = torch.randn(2,2,2,3)#第二个2对应BatchNorm2d(2,affine=True)中的2,表示通道数目 output = m(input) print("输入图片:") print(input) print("归一化权重:") print(m.weight.shape)#[2] print(m.weight) print("归一化的偏重:") print(m.bias.shape)#[2] print(m.bias) print("归一化的输出:") print(output) print("输出的尺度:") print(output.size()) print("输入的第一个维度:") A = input[0][0] B = input[1][0] print(A) print(B) C =torch.cat([A,B],dim=0)#纵向拼接,BN按通道处理 print(C) firstDimenMean = torch.Tensor.mean(C) firstDimenVar= torch.Tensor.var(C,False) #Bessel's Correction贝塞尔校正不会被使用 print(m.eps) print("输入的第一个维度平均值:") print(firstDimenMean) print("输入的第一个维度方差:") print(firstDimenVar) bacthnormone = \ ((input[0][0][0][0] - firstDimenMean)/(torch.pow(firstDimenVar,0.5)+m.eps ))\ * m.weight[0] + m.bias[0] print(bacthnormone)#-0.3023对output[0][0][0][0]
输入图片: tensor([[[[ 0.0242, -0.4434, 0.0058], [-0.2674, 1.8737, 1.8069]], [[-0.3274, -0.7689, 0.3982], [ 0.7088, -0.4982, 1.3230]]], [[[-2.0022, 1.2179, 1.0144], [-0.0057, 0.3186, 0.4562]], [[ 0.3482, -0.0875, -1.1406], [ 1.5080, 0.8830, 0.0946]]]]) 归一化权重: torch.Size([2]) Parameter containing: tensor([1., 1.], requires_grad=True) 归一化的偏重: torch.Size([2]) Parameter containing: tensor([0., 0.], requires_grad=True) 归一化的输出: tensor([[[[-0.3023, -0.7597, -0.3203], [-0.5875, 1.5068, 1.4414]], [[-0.6781, -1.2420, 0.2489], [ 0.6456, -0.8962, 1.4301]]], [[[-2.2844, 0.8653, 0.6663], [-0.3316, -0.0144, 0.1203]], [[ 0.1849, -0.3717, -1.7169], [ 1.6665, 0.8681, -0.1391]]]], grad_fn=<NativeBatchNormBackward>) 输出的尺度: torch.Size([2, 2, 2, 3]) 输入的第一个维度: tensor([[ 0.0242, -0.4434, 0.0058], [-0.2674, 1.8737, 1.8069]]) tensor([[-2.0022, 1.2179, 1.0144], [-0.0057, 0.3186, 0.4562]]) tensor([[ 0.0242, -0.4434, 0.0058], [-0.2674, 1.8737, 1.8069], [-2.0022, 1.2179, 1.0144], [-0.0057, 0.3186, 0.4562]]) 1e-05 输入的第一个维度平均值: tensor(0.3332) 输入的第一个维度方差: tensor(1.0452) tensor(-0.3023, grad_fn=<AddBackward0>)
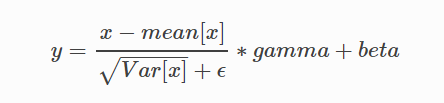

 浙公网安备 33010602011771号
浙公网安备 33010602011771号