PAt 1099
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
- Both the left and right subtrees must also be binary search trees.
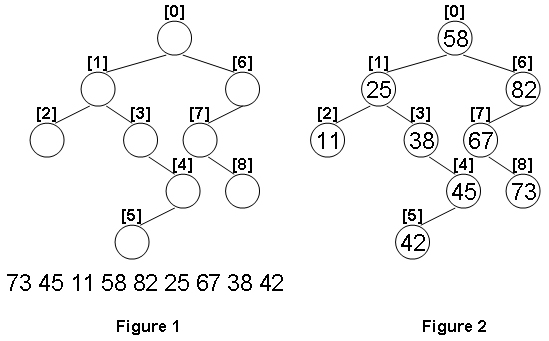
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then − will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.
Output Specification:
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.
Sample Input:
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
Sample Output:
58 25 82 11 38 67 45 73 42
//根据二叉树的结构和中序遍历来写出层序遍历 #include <bits/stdc++.h> using namespace std; #define N 120 #define P pair<int,int> struct Tree{ int val,l,r; Tree(){ } Tree(int val,int l,int r):val(val),l(l),r(r){ } }tr[N]; int a[N],b[N],n; //不需要建树,题目输入的就是了 int cnt2=0; void search(int rt){//中序 if(rt==-1) return ; search(tr[rt].l); tr[rt].val=a[cnt2++]; search(tr[rt].r); } int cnt = 0; void dfs(int rt){//层序遍历 queue<P>q; q.push(P(rt,tr[rt].val)); int flag =1; while(!q.empty()){ P p =q.front();q.pop(); int x=p.first,y=p.second; //输出格式 if(flag){ printf("%d",y); flag =0; } else{ printf(" %d",y); } int num1 = tr[x].l; int num2= tr[x].r; if(num1!=-1){ q.push(P(num1,tr[num1].val)); } if(num2!=-1){ q.push(P(num2,tr[num2].val)); } } } int main() { scanf("%d",&n); for(int i =0;i<n;i++){ scanf("%d%d",&tr[i].l,&tr[i].r); } for(int i =0;i<n;i++) scanf("%d",&a[i]); sort(a,a+n); search(0); dfs(0); return 0; }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步