关联分析中的支持度、置信度和提升度

1.支持度（Support）

    支持度表示项集{X,Y}在总项集里出现的概率。公式为：

              Support(X→Y) = P(X,Y) / P(I) = P(X∪Y) / P(I) = num(XUY) / num(I)

 其中，I表示总事务集。num()表示求事务集里特定项集出现的次数。  

            比如，num(I)表示总事务集的个数

                        num(X∪Y)表示含有{X,Y}的事务集的个数（个数也叫次数）。    

2.置信度 （Confidence）

   置信度表示在先决条件X发生的情况下，由关联规则”X→Y“推出Y的概率。即在含有X的项集中，含有Y的可能性，公式为：

               Confidence(X→Y) = P(Y|X)  = P(X,Y) / P(X) = P(XUY) / P(X) 

3.提升度（Lift）

    提升度表示含有X的条件下，同时含有Y的概率，与Y总体发生的概率之比。

               Lift(X→Y) = P(Y|X) / P(Y)

     例1，已知有1000名顾客买年货，分为甲乙两组，每组各500人，其中甲组有500人买了茶叶，同时又有450人买了咖啡；乙组有450人买了咖啡，如表（1）所示：

 

 

 

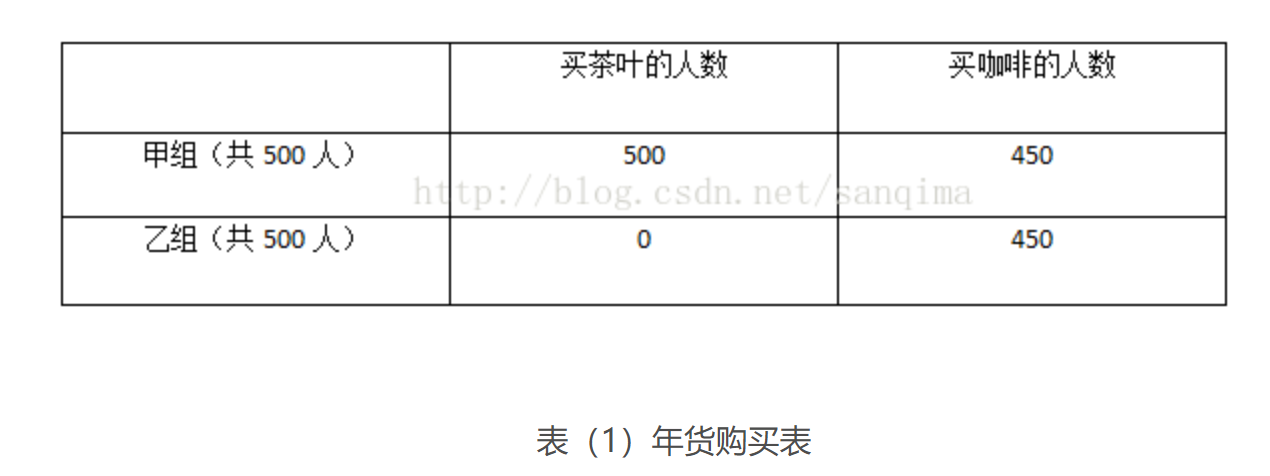
表（1）年货购买表

      试求解 1）”茶叶→咖啡“的支持度          #  既买了茶叶又买了咖啡的人/购物人数总数  = 450 / 1000= 0.45 

                   2) "茶叶→咖啡"的置信度          #  既买了茶叶又买了咖啡的人/购买了茶叶人数总数  = 450/500 = 0.9

                   3）”茶叶→咖啡“的提升度         #  在购买了茶叶情况下同时购买了咖啡的概率（其实就是上面的置信度）/购买了咖啡的概率[（450+450）/（500+500）  =  0.9 / 0.9 = 1

    分析：

         设X= {买茶叶}，Y={买咖啡}，则规则”茶叶→咖啡“表示”即买了茶叶，又买了咖啡“，于是，”茶叶→咖啡“的支持度为

               Support(X→Y) = 450 / （500+500) = 45%      # 此处跟原创文章不一样，原创应该是笔误，答案应该是 0.45 

        "茶叶→咖啡"的置信度为

               Confidence(X→Y) = 450 / 500 = 90%

          ”茶叶→咖啡“的提升度为

               Lift(X→Y) = Confidence(X→Y) / P(Y) = 90% /  ((450+450) / 1000) = 90% / 90% = 1

         由于提升度Lift(X→Y) =1，表示X与Y相互独立，即是否有X，对于Y的出现无影响。也就是说，是否购买咖啡，与有没有购买茶叶无关联。即规则”茶叶→咖啡“不成立，或者说关联性很小，几乎没有，虽然它的支持度和置信度都高达90%，但它不是一条有效的关联规则。

 

判断关联规则是否有效的因素：

        满足最小支持度和最小置信度的规则，叫做“强关联规则”（这个在我们设置算法的时候参数就会设定好）。然而，强关联规则里，也分有效的强关联规则和无效的强关联规则。

        如果Lift(X→Y)>1，则规则“X→Y”是有效的强关联规则。

        如果Lift(X→Y) <=1，则规则“X→Y”是无效的强关联规则。

        特别地，如果Lift(X→Y) =1，则表示X与Y相互独立。

 

原文链接：https://blog.csdn.net/sanqima/article/details/42746419