《机器学习》第一次作业——第一至三章学习记录和心得
第一章模式识别基本概念
1.1 什么是模式识别
模式识别分为以下两种模式:
- 分类——输出是离散的类别表示,即输出待识别模式所属的类别;有二类/多类
- 回归——输出量是连续的信号表达(回归值);输出量是单个/多个维度
回归是分类的基础:离散的类别值是由回归值做判别决策得到的。
- 模式识别本质上是一种推理(inference)过程。
1.2 模式识别数学表达
数学解释——模式识别可以看做一种函数映射f(x)

模型——关于已有知识的一种表达方式,即函数y=f(x)
- 特征提取
- 回归器——将特征映射到回归值

判别函数——用特定的非线性函数实现,判别器有二类分类和多累分类;判别函数不能当做模型的一部分
判别公式和决策边界——用来分类
特征
- 特征的特征——辨别能力
- 特征的特性——鲁棒性
- 特征向量——模长(标量)×方向(单位向量)
- 特征空间
1.3 特征向量的相关性
度量特征向量两两之间的相关性是识别模式之间是否相似的基础
点积
- 代数定义(标量、对称性,线性变化)
- 几何定义(可体现方向上的相似度)
投影——将向量想垂直投射到向量y方向上的长度;不具备对称性
- 点积可通过投影表达
残差向量——向量x分解到y方向上得到的投影向量与原向量x的误差
欧氏距离——表征两个向量之间的相似程度(综合考虑方向和横长)
1.4 机器学习基本概念


线性模型——线性的(直线、面、超平面)
非线性模型——(曲面、曲线、超曲面)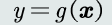
常见非线性模型:多项式、神经网络、决策树...
训练样量N与模型参数的关系
- N=M:参数有唯一解
- N>>M:没有准确的解(over-determined)
- N<<M:无数个解/无解
优化算法——最小化或最大化目标函数
机器学习方式
- 监督式学习——训练样本及其输出真值都给定情况下的机器学习算法
- 无监督式学习——只给定训练样本、没有给输出真值情况下的机器学习算法;算法难度远高于监督式学习;应用于聚类、图像分割
- 半监督式学习——既有标注的训练样本、又有未标注的训练样本情况下的学习算法
1.5 模型泛化能力
泛化能力——训练得到的模型不仅要对训练样本具有决策能力,也要对新的(训练过程中未看见)的模式具有决策能力。
提高泛化能力——不要过度训练。
- 选择复杂度适合的模型
- 在目标函数中加入正则项来实现
1.6 评估方法与性能指标
评估方法
- 留出法(Hold-out)——随机划分;将数据集随机分为两组:训练集和测试集。利用训练集训练模型,然后利用测试集评估模型的量化指标。
- K折交叉验证(K-Folds Cross Validation)——将数据集分割成K个子集,从其中选取单个子集作为测试集,其他K - 1个子集作为训练集。
- 留一验证(leave- one-out cross-validation)——每次只取数据集中的一个样本做测试集,剩余的做训练集。
性能指标度量

F-Score——
曲线度量——PR曲线、ROC曲线、曲线下方面积AUC
第二章基于距离的分类器
2.1 MED分类器
基于距离的决策——把测试样本到每个类之间的距离作为决策模型,将测试样本判定为与其距离最近的类。
类的原型——用来代表这个类的一个模式或者一组量,便于计算该类和测试样本之间的距离
距离度量

MED分类器
- 概念——最小欧式距离分类器(Minimum Euclidean Distance Classifier)
- 距离衡量——欧式距离
- 类的原型——均值
- 决策边界——
![]()
- 存在的问题——MED分类器采用欧氏距离作为距离度量,没有考虑特征变化的不同及特征之间的相关性。
- 解决方法——特征白化
2.3 特征白化
目的——去除特征变化的不同特性及特征之间的相关性
步骤——先去除特征之间的相关性(解耦, Decoupling),然后再对特征进行尺度变换(白化,Whitening),使每维特征的方差相等。
令W=W2W1
- 解耦——通过WW实现协方差矩阵对角化,去除特征之间的相关性。
- 白化——通过W2W2对上一步变换后的特征再进行尺度变换,实现所有特征具有相同方差。
2.3 MICD分类器
MICD分类器
- 概念——最小类内距离分类器(Minimum Intra-class Distance Classifier) ,基于马氏距离的分类器。
- 距离度量——马氏距离
- 类的原型——均值
- 缺陷——会选择方差较大的类
第三章贝叶斯决策与学习
3.1贝叶斯决策与MAP分类器
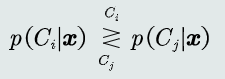
基于贝叶斯规则,计算后验概率

MAP分类器(最大后验概率分类器)——将测试样本决策分类给后验概率最大的那个类

给定所有测试样本,MAP分类器选择后验概率最大的类,等于最小化平均概率误差即最小化决策误差
3.2 MAP分类器:高斯观测概率
1、表达先验和观测概率的方式
- 常数表达:例如,𝑝 𝐶𝑖 = 0.2
- 参数化解析表达:高斯分布……
- 非参数化表达:直方图、核密度、蒙特卡洛…
 代入MAP分类器判别公式并化简得
代入MAP分类器判别公式并化简得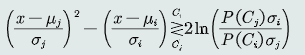 ;为了得到决策边界,设置判别公式两边相等
;为了得到决策边界,设置判别公式两边相等


- 和MICD、MED分类器相比,MAP分类器偏向于先验可能性比较大的类、分布较为紧致的类。
3.3 决策风险与贝叶斯分类器
决策风险——贝叶斯决策可能会出现错误判断,并且不同的错误决策会产生程度完全不一样的风险
- 因此引入损失(loss)的概念,针对决策进行损失评估;
贝叶斯决策的期望损失——所有样本的决策损失之和![]()
- 决策目标:最小化期望损失,即对每个测试样本选择风险最小的类
贝叶斯分类器——在MAP分类器基础上,加入决策风险因素;给定一个测试样本x,贝叶斯分类器选择风险最小的类
- 判别公式:
![]()
朴素贝叶斯分类器——假设特征之间是相互独立,从而推出以下公式
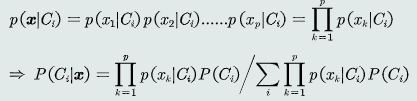
决策边界附近的处理——为避免错误决策,分类器可以拒绝
3.4 最大似然估计
常用的参数估计方法
- 最大似然估计
- 贝叶斯估计
先验概率估计
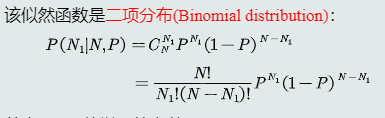 P为待学习的参数
P为待学习的参数
- 先验概率的最大似然估计就是该类训练样本出现的频率
- 高斯分布均值的最大似然估计等于样本的均值
- 高斯分布协方差的最大似然估计等于所有训练模式的协方差
3.5 最大似然的估计偏差
无偏估计——如果一个参数的估计量的数学期望是该参数的真值,则该估计量为无偏估计
这意味着训练样本个数足够多,该估计值就是参数的真实值
最大似然估计

3.6 &3.7 贝叶斯估计
贝叶斯估计——给定参数分布的先验概率以及训练样本,估计参数分布的后验概率
高斯观测似然

假设参数的先验概率分布也服从单位高斯分布,根据先验概率和基于训练样本的观测似然,计算后验概率,可以解出

分析
- 给定𝐶𝑖类的𝑁𝑖个训练样本,参数θ概率分布的均值等于训练样本均值和该参数先验概率均值的加权和。
- 给定𝐶𝑖类的𝑁𝑖个训练样本,参数θ概率分布的方差是由𝐶𝑖类观测似然分布的方差、该参数的先验概率方差、 𝐶𝑖类的样本个数共同决定
- 当Ni足够大时,样本均值m就是参数θ的无偏估计
参数先验对后验的影响
- 如果参数的先验方差𝜎0 = 0,则𝜇𝜃 → 𝜇0,意味先验的确定性较大,先验均值的影响也更大,使得后续训练样本的不断进入对参数估计没有太多改变。
- 如果参数的先验方差𝜎0 ≫ 𝜎,则𝜇𝜃 → 𝑚,意味着先验的确定性非常小。刚开始由于样本较少,导致参数估计不准。随着样本的不断增加,后验均值会逼近样本均值。
贝叶斯具备不断学习的能力
观测似然概率的估计
参数为随机参数,观测似然通过求边缘概率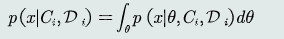 ;由于各个类别单独估计概率分布,上式写为
;由于各个类别单独估计概率分布,上式写为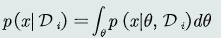


贝叶斯估计与最大似然估计
- 贝叶斯估计把𝜃当做隐随机变量,所以需要求关于𝜃 的边缘概率,从而来得到观测似然;而最大似然估计有明确的目标函数,通过优化技术来求取𝜃 ML
3.8 KNN估计
常用的无参数技术
- K近邻法(K-nearest neighbors)
- 直方图技术(Histogram technique)
- 核密度估计(Kernel density estimation)
概率密度估计基本理论
给定𝑁个训练样本,在特征空间内估计每个任意取值𝒙的概率密度,即估计以𝒙为中心、在极小的区域𝑅 = (𝒙, 𝒙 + 𝛿𝒙) 内的概率密度函数𝑝(𝒙);
- 无参数估计的任务: 估计概率𝑝(𝒙)。
- 如果区域𝑅足够小,𝑃是𝑝(𝒙)的平滑版本,可以用来估计𝑝(𝒙)。
![]()
![]() k个样本落在区域R内的概率密度可以用二项分布表达
k个样本落在区域R内的概率密度可以用二项分布表达![]() 当N很大时,k的分布非常尖锐且集中在均值附近;二项分布的均值
当N很大时,k的分布非常尖锐且集中在均值附近;二项分布的均值![]()
![]() ;因此N很大时,可用均值表达k的分布;得到P的近似估计
;因此N很大时,可用均值表达k的分布;得到P的近似估计

KNN估计(K近邻估计)——给定x,找到其对应的区域R使其包含k个训练样本,以此计算p(x)
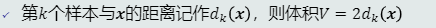 概率密度表达为:
概率密度表达为: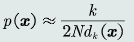
训练样本个数N越大,k取值越大,概率估计的越准确
- 优点:可以自适应的确定x相关的区域R的范围。
- 缺点:KNN概率密度估计不是连续函数,计算出的概率并不是真正的概率密度表达,积分回到正无穷而不是1。在推理测试阶段仍然需要存储所有训练样本,且易受噪声影响。
3.9 直方图与核密度估计
直方图估计
- 优点:减少由于噪声污染造成的估计误差;不需要存储训练样本
- 缺点:估计可能不准确;缺乏概率估计的自适应能力,导致过于尖锐或平滑
核密度估计

估计对比
- KNN估计:以待估计的任意一个模式为中心,搜寻第𝑘个近邻点,以此来确定区域,易被噪声污染。
- 直方图估计:手动将特征空间划分为若干个区域,待估计模式只能分配到对应的固定区域,缺乏自适应能力


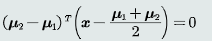


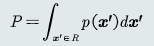 k个样本落在区域R内的概率密度可以用二项分布表达
k个样本落在区域R内的概率密度可以用二项分布表达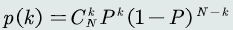 当N很大时,k的分布非常尖锐且集中在均值附近;二项分布的均值
当N很大时,k的分布非常尖锐且集中在均值附近;二项分布的均值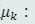
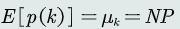 ;因此N很大时,可用均值表达k的分布;得到P的近似估计
;因此N很大时,可用均值表达k的分布;得到P的近似估计
 浙公网安备 33010602011771号
浙公网安备 33010602011771号