异常检测:探索数据深层次背后的奥秘《中篇》
异常检测:探索数据深层次背后的奥秘《中篇》
1.异常检测——线性相关方法
真实数据集中不同维度的数据通常具有高度的相关性,这是因为不同的属性往往是由相同的基础过程以密切相关的方式产生的。在古典统计学中,这被称为——回归建模,一种参数化的相关性分析。
一类相关性分析试图通过其他变量预测单独的属性值,另一类方法用一些潜在变量来代表整个数据。前者的代表是 线性回归,后者一个典型的例子是 主成分分析。本文将会用这两种典型的线性相关分析方法进行异常检测。
需要明确的是,这里有两个重要的假设:
假设一:近似线性相关假设。线性相关假设是使用两种模型进行异常检测的重要理论基础。
假设二:子空间假设。子空间假设认为数据是镶嵌在低维子空间中的,线性方法的目的是找到合适的低维子空间使得异常点(o)在其中区别于正常点(n)。
基于这两点假设,在异常检测的第一阶段,为了确定特定的模型是否适合特定的数据集,对数据进行探索性和可视化分析是非常关键的。
- 线性回归
在线性回归中,我们假设不同维度的变量具有一定的相关性,并可以通过一个相关系数矩阵进行衡量。因此对于特定的观测值,可以通过线性方程组来建模。在实际应用中,观测值的数量往往远大于数据的维度,导致线性方程组是一个超定方程,不能直接求解。因此需要通过优化的方法,最小化模型预测值与真实数据点的误差。
线性回归是统计学中一个重要的应用,这个重要的应用往往是指通过一系列自变量去预测一个特殊因变量的值。在这种情况下,异常值是根据其他自变量对因变量的影响来定义的,而自变量之间相互关系中的异常则不那么重要。这里的异常点检测主要用于数据降噪,避免异常点的出现对模型性能的影响,因而这里关注的兴趣点主要是正常值(n)。
而我们通常所说的异常检测中并不会对任何变量给与特殊对待,异常值的定义是基于基础数据点的整体分布,这里我们关注的兴趣点主要是异常值(o)。
广义的回归建模只是一种工具,这种工具既可以用来进行数据降噪也可以进行异常点检测。
1.1 基于自变量与因变量的线性回归
1.1.1 最小二乘法
为了简单起见,这里我们一元线性回归为例:
$$Y=\sum_{i=1}^{d} a_{i} \cdot X_{i}+a_{d+1}$$
变量Y为因变量,也就是我们要预测的值;$X_{1}...X_{d}$为一系列因变量,也就是输入值。系数$a_{1}...a_{d+1}$为要学习的参数。假设数据共包含$N$个样本,第$j$个样本包含的数据为$x_{j1}...x_{jd}$和$y_{j}$,带入式(1)如下式所示:
$$y_{j}=\sum_{i=1}^{d} a_{i} \cdot x_{j i}+a_{d+1}+\epsilon_{j}$$
这里$\epsilon_{j}$为第$j$个样本的误差。以$Y$ 代表 $N \times 1$ 的因变量矩阵${(y_{1}...y_{N})}^{T}$,即样本中的真实值;以$U$代表$N \times (d+1)$的自变量矩阵,其中第$j$行为$(x_{j1}...x_{jd}, 1)$;以$A$ 代表 $(d+1) \times 1$ 的系数矩阵$(a_{1}...a_{d+1})^{T}$。则模型可表示为:
$$f(U, A) = U \cdot A$$
定义目标函数为:
$$L(A) = \frac{1}{2}{\left| {Y - U \cdot A} \right|^2} $$
目标函数是关于$A$的凸函数,其对$A$求偏导为:
$$\frac{{\partial L(A)}}{{\partial A}} = \frac{1}{2}\frac{{\partial {{\left| {Y - U \cdot A} \right|}^2}}}{{\partial A}} = - {U^T}(Y - U \cdot A)$$
令$\frac{{\partial L(A)}}{{\partial A}}=0$,得到最优参数为:
$$A=\left(U^{T} \cdot U\right)^{-1} \cdot\left(U^{T} \cdot Y\right)$$
这种求解线性回归参数的方法也叫最小二乘法。
最小二乘法要求矩阵 $U^{T} \cdot U$ 可逆,即$U^{T} \cdot U$是满秩的。当$U^{T} \cdot U$不可逆时可以通过两种方法进行参数估计,一种先使用主成分分析等方法来预处理数据,消除不同特征之间的相关性,然后再使用最小二乘法。第二种方法是使用梯度下降法。
1.1.2 梯度下降法
数据集
监督学习一般靠数据驱动。我们通常收集一系列的真实数据,例如多栋房屋的真实售出价格和它们对应的面积和房龄。我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里,该数据集被称为训练数据集(training data set)或训练集(training set),通常还应该有一个用于防止过拟合的交叉验证集和一个用于评估模型性能的测试集(test set)。一栋房屋被称为一个样本(sample),其真实售出价格叫作标签(label),用来预测标签的两个因素叫作特征(feature)。
损失函数
如果把线性回归看作是一个优化问题,那么我们要优化的目标就是损失函数。损失函数是用来衡量样本误差的函数,我们的优化目标是要求得在误差最小的情况下模型参数的值。这里强调一下损失函数和代价函数的区别:
注意:
Loss Function(损失函数):the error for single training example;
Cost Function(代价函数):the average of the loss functions of the entire training set;
线性回归常用的损失函数是均方误差,表达式为:
$$l^{(i)}(\mathbf{w}, b)=\frac{1}{2}\left(\hat{y}{(i)}-y\right)^{2}$$
$$
L(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} l^{(i)}(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}\left(\mathbf{w}^{\top} \mathbf{x}{(i)}+b-y\right)^{2}
$$
其中 $\hat{y}$ 为预测值,$y$ 为真实值。
优化算法 - 随机梯度下降
当模型和损失函数形式较为简单时,上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解(analytical solution)。本节使用的线性回归和平方误差刚好属于这个范畴。然而,大多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
在求数值解的优化算法中,小批量随机梯度下降(mini-batch stochastic gradient descent)被广泛使用。它的算法很简单:先选取一组模型参数的初始值,如随机选取;接下来对参数进行多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch),然后求小批量中数据样本的平均损失和有关模型参数的导数(梯度),最后用此结果与预先设定的学习率的乘积作为模型参数在本次迭代的减小量。如下式所示:
$$
(\mathbf{w}, b) \leftarrow(\mathbf{w}, b)-\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w}, b)} l^{(i)}(\mathbf{w}, b)
$$
学习率($\eta$): 代表在每次优化中,能够学习的步长的大小
批量大小($B$): 是小批量计算中的批量大小batch size
1.2 基于异常检测的线性回归
前一节讨论了这样一种情况:即一个特定的变量被认为是特殊的,最优平面是通过最小化该特殊变量的均方误差而确定的。而我们通常所说的异常检测中并不会对任何变量给与特殊对待,异常值的定义是基于基础数据点的整体分布,因此需要采用一种更一般的回归建模:即以相似的方式对待所有变量,通过最小化数据对该平面的投影误差确定最佳回归平面。在这种情况下,假设我们有一组变量 $X_{1}… X_{d}$, 对应的回归平面如下:
$$a_{1} \cdot X_{1}+\ldots+a_{d} \cdot X_{d}+a_{d+1}=0$$
为了后续计算的方便,对参数进行如下约束:
$$\sum\limits_{i = 1}^d {a_i^2 = 1} $$
以$L_{2}$范数作为目标函数:
$$L = {\left| {U \cdot A} \right|_2}$$
这样的一个问题可以通过主成分分析方法得到有效解决,我们会单独用一个部分进行讨论。
2.主成分分析
上一节的最小二乘法试图找到一个与数据具有最佳匹配 $(d−1)$ 维超平面。主成分分析方法可用于解决这一问题的广义版本。具体来说,它可以找到任意 $k( k<d )$ 维的最优表示超平面,从而使平方投影误差最小化。
2.1 原理推导
对于 $d$ 维,包含 $N$ 个样本的数据,用 $R_{i}$ 表示其中第 $i$ 行为:$[x_{i1}... x_{id}]$。由此可以得到 $d \times d$ 的协方差矩阵(标准的PCA应当计算相关系数矩阵,即对数据进行均值为0方差为1的标准化处理,而协方差矩阵只需要减去均值即可):
$$Σ = (R - \bar{R})^{T} \cdot (R - \bar{R}) $$
易知协方差矩阵 $Σ$ 是对称并且半正定的,因此可以进行相似对角化:
$$Σ = P \cdot D \cdot P^{T}$$
这里的 $D$ 为对角矩阵,对角元素为特征值;$P$ 为标准正交矩阵,每一行为对应的特征向量;这些标准正交向量提供了数据应该投影的轴线方向。与异常检测相关的主成分分析的主要性质如下:
-
如果前 $k$ 的特征向量选定之后(根据最大的$k$个特征值),由这些特征向量定义的 $k$ 维超平面是在所有维度为 $k$ 的超平面中,所有数据点到它的均方距离尽可能小的平面。
-
如果将数据转换为与正交特征向量对应的轴系,则转换后的数据沿每个特征向量维的方差等于相应的特征值。在这种新表示中,转换后的数据的协方差为0。
-
由于沿特征值小的特征向量的转换数据的方差很低,因此沿这些方向的变换数据与平均值的显着偏差可能表示离群值。
需要注意的是,相比2.2节的内容,这里提供了一个更加普遍的解决方法。2.2中的内容可以归为主成分分析中只保留最大特征值对应的特征向量的情况。
在得到这些特征值和特征向量之后,可以将数据转换到新的坐标系中。以 $Y_{1}...Y_{N}$ 表示新坐标系中的数据,这些数据可以通过原始向量 $R_{i}$ 与包含新轴系的标准正交特征向量矩阵 $P$ 的乘积来实现。
$${Y_i} = {R_i} \cdot P$$
在许多涉及高维数据集的真实场景中,很大一部分特征值往往非常接近于零。这意味着大多数数据都沿着一个低维的子空间排列。从异常检测的角度来看,这是非常方便的,因为离这些投影方向非常远的观测值可以被假定为离群值。例如,对于特征值较小(方差较小)的特征向量 $j$,第 $i$ 条记录的 $y_{ij}$ 与 $y_{kj}$ 的其他值的偏差较大,说明有离群行为。这是因为当$j$固定而$k$变化时,$y_{kj}$ 的值应当变化不大。因此,$y_{ij}$ 值是不常见的。
在不选取任何特定的 $k$ 维集合的情况下,一种更精确的异常检测建模方法是使用特征值来计算数据点沿每个主分量方向到质心的归一化距离。设 $e_{j}$为第 $j$ 个特征向量,$λ_{j}$ 为沿该方向的方差(特征值)。数据点$\bar{X}$相对于对数据质心$\bar{\mu} $的总体归一化异常得分可以由下式给出:
$$S \operatorname{core}(\bar{X})=\sum_{j=1}^{d} \frac{\left|(\bar{X}-\bar{\mu}) \cdot \bar{e}{j}\right|^{2}}{\lambda{j}}$$
值得注意的是,对异常得分的大部分贡献是由 $λ_{j}$ 值较小的主成分的偏差提供的,这一点上文中有提及过。主成分分析比因变量回归能更稳定地处理少数异常值的存在。这是因为主成分分析是根据最优超平面来计算误差的,而不是一个特定的变量。当数据中加入更多的离群点时,最优超平面的变化通常不会大到影响离群点的选择。因此,这种方法更有可能选择正确的异常值,因为回归模型一开始就更准确。
2.2 归一化问题
当不同维度的尺度差别较大时,使用 $PCA$ 有时并不能得到直观有效的结果。例如,考虑一个包含年龄和工资等属性的人口统计数据集。工资属性的范围可能是几万,而年龄属性几乎总是小于100,使用主成分分析会导致主成分被高方差属性所控制。对于一个只包含年龄和工资的二维数据集,最大的特征向量几乎与工资轴平行,这会降低异常点检测过程的有效性。因此,一个自然的解决方案是对数据进行均值为0方差为1的标准化处理。这隐含地导致在主成分分析中使用相关矩阵而不是协方差矩阵。当然,这个问题并不是线性建模所独有的,对于大多数异常检测算法,都需要使用这样的预处理。
2.3、回归分析的局限性
回归分析作为检测离群值的工具有一些局限性。这些缺点中最重要的是在本章的一开始就讨论了,其中探讨了回归分析的数据特定性质。特别是,为了使回归分析技术有效,数据需要高度相关,并沿着低维子空间对齐。当数据不相关,但在某些区域高度聚集时,这种方法可能不会有效。
另一个相关的问题是,数据中的相关性在本质上可能不是全局性的。子空间相关性可能是特定于数据的特定位置的。在这种情况下,由主成分分析发现的全局子空间对于异常检测是次优的。因此,为了创建更一般的局部子空间模型,有时将线性模型与邻近模型结合起来是有用的。
- 小结 总结
真实数据中,数据不同属性之间往往具有显著的相关性。在这种情况下,线性建模可以提供一种有效的工具来从底层数据中移除异常值或者进行异常检测。对于其他基于因变量回归的应用,线性建模是一种工具,去除异常值对于提高此类应用的性能是非常重要的。在大多数情况下,主成分分析提供了去除异常值和进行异常检测最有效的方法,因为它对存在少数异常值的数据更有鲁棒性。
- 参考资料
[1] 《Outlier Analysis》——Charu C. Aggarwal
[2] Anomaly Detection: A Survey VARUN CHANDOLA, ARINDAM BANERJEE, and VIPIN KUMAR University of Minnesota
[3] Anomaly Detection: A Tutorial
[4] Data Mining Concepts and Techniques Third Edition
3.异常检测——基于相似度的方法
“异常”通常是一个主观的判断,什么样的数据被认为是“异常”的,需要结合业务背景和环境来具体分析确定。
实际上,数据通常嵌入在大量的噪声中,而我们所说的“异常值”通常指具有特定业务意义的那一类特殊的异常值。噪声可以视作特性较弱的异常值,没有被分析的价值。噪声和异常之间、正常数据和噪声之间的边界都是模糊的。异常值通常具有更高的离群程度分数值,同时也更具有可解释性。
在普通的数据处理中,我们常常需要保留正常数据,而对噪声和异常值的特性则基本忽略。但在异常检测中,我们弱化了“噪声”和“正常数据”之间的区别,专注于那些具有有价值特性的异常值。在基于相似度的方法中,主要思想是异常点的表示与正常点不同
3.1、基于距离的度量
基于距离的方法是一种常见的适用于各种数据域的异常检测算法,它基于最近邻距离来定义异常值。 此类方法不仅适用于多维数值数据,在其他许多领域,例如分类数据,文本数据,时间序列数据和序列数据等方面也有广泛的应用。
基于距离的异常检测有这样一个前提假设,即异常点的 $k$ 近邻距离要远大于正常点。解决问题的最简单方法是使用嵌套循环。 第一层循环遍历每个数据,第二层循环进行异常判断,需要计算当前点与其他点的距离,一旦已识别出多于 $k$ 个数据点与当前点的距离在 $D$ 之内,则将该点自动标记为非异常值。 这样计算的时间复杂度为$O(N^{2})$,当数据量比较大时,这样计算是及不划算的。 因此,需要修剪方法以加快距离计算。
3.1.1 基于单元的方法
在基于单元格的技术中,数据空间被划分为单元格,单元格的宽度是阈值D和数据维数的函数。具体地说,每个维度被划分成宽度最多为 $\frac{D}{{2 \cdot \sqrt d }}$ 单元格。在给定的单元以及相邻的单元中存在的数据点满足某些特性,这些特性可以让数据被更有效的处理。
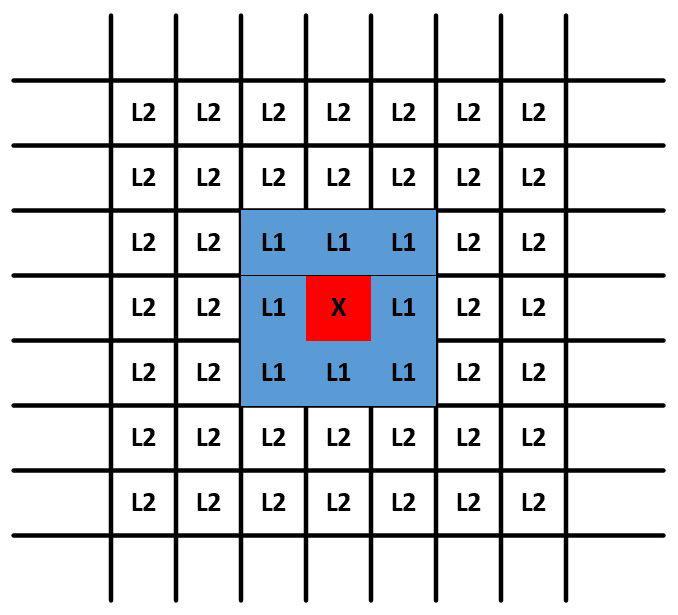
以二维情况为例,此时网格间的距离为 $\frac{D}{{2 \cdot \sqrt d }}$ ,需要记住的一点是,网格单元的数量基于数据空间的分区,并且与数据点的数量无关。这是决定该方法在低维数据上的效率的重要因素,在这种情况下,网格单元的数量可能不多。 另一方面,此方法不适用于更高维度的数据。对于给定的单元格,其 $L_{1}$ 邻居被定义为通过最多1个单元间的边界可从该单元到达的单元格的集合。请注意,在一个角上接触的两个单元格也是 $L_{1}$ 邻居。 $L_{2}$ 邻居是通过跨越2个或3个边界而获得的那些单元格。 上图中显示了标记为 $X$的特定单元格及其 $L_{1}$ 和 $L_{2}$ 邻居集。 显然,内部单元具有8个 $L_{1}$ 邻居和40个 $L_{2}$ 邻居。 然后,可以立即观察到以下性质:
- 单元格中两点之间的距离最多为 $D/2$。
- 一个点与 $L_{1}$ 邻接点之间的距离最大为 $D$。
- 一个点与它的 $Lr$ 邻居(其中$r$ > 2)中的一个点之间的距离至少为$D$。
唯一无法直接得出结论的是 $L_{2}$ 中的单元格。 这表示特定单元中数据点的不确定性区域。 对于这些情况,需要明确执行距离计算。 同时,可以定义许多规则,以便立即将部分数据点确定为异常值或非异常值。 规则如下:
- 如果一个单元格中包含超过 $k$ 个数据点及其 $L_{1}$ 邻居,那么这些数据点都不是异常值。
- 如果单元 $A$ 及其相邻 $L_{1}$ 和 $L_{2}$ 中包含少于 $k$ 个数据点,则单元A中的所有点都是异常值。
此过程的第一步是将部分数据点直接标记为非异常值(如果由于第一个规则而导致它们的单元格包含 $k$ 个点以上)。 此外,此类单元格的所有相邻单元格仅包含非异常值。 为了充分利用第一条规则的修剪能力,确定每个单元格及其 $L_{1}$ 邻居中点的总和。 如果总数大于 $k$ ,则所有这些点也都标记为非离群值。
接下来,利用第二条规则的修剪能力。 对于包含至少一个数据点的每个单元格 $A$,计算其中的点数及其 $L_{1}$ 和 $L_{2}$ 邻居的总和。 如果该数字不超过 $k$,则将单元格$A$ 中的所有点标记为离群值。 此时,许多单元可能被标记为异常值或非异常值。
对于此时仍未标记为异常值或非异常值的单元格中的数据点需要明确计算其 $k$ 最近邻距离。即使对于这样的数据点,通过使用单元格结构也可以更快地计算出 $k$ 个最近邻的距离。考虑到目前为止尚未被标记为异常值或非异常值的单元格$A$。这样的单元可能同时包含异常值和非异常值。单元格 $A$ 中数据点的不确定性主要存在于该单元格的 $L_{2}$ 邻居中的点集。无法通过规则知道 $A$ 的 $L_{2}$ 邻居中的点是否在阈值距离 $D$ 内,为了确定单元 $A$ 中数据点与其$L_{2}$ 邻居中的点集在阈值距离 $D$ 内的点数,需要进行显式距离计算。对于那些在 $L_{1}$ 和 $L_{2}$ 中不超过 $k$ 个且距离小于 $D$ 的数据点,则声明为异常值。需要注意,仅需要对单元 $A$ 中的点到单元$A$的$L_{2}$邻居中的点执行显式距离计算。这是因为已知 $L_{1}$ 邻居中的所有点到 $A$ 中任何点的距离都小于 $D$,并且已知 $Lr$ 中 $(r> 2)$ 的所有点与 $A$上任何点的距离至少为 $D$。因此,可以在距离计算中实现额外的节省。
3.1.2 基于索引的方法
对于一个给定数据集,基于索引的方法利用多维索引结构(如 $\mathrm{R}$ 树、$k-d$ 树)来搜索每个数据对象 $A$ 在半径 $D$ 范围 内的相邻点。设 $M$ 是一个异常值在其 $D$ -邻域内允许含有对象的最多个数,若发现某个数据对象 $A$ 的 $D$ -邻域内出现 $M+1$ 甚至更多个相邻点, 则判定对象 $A$ 不是异常值。该算法时间复杂度在最坏情况下为 $O\left(k N^{2}\right),$ 其中 $k$ 是数据集维数, $N$ 是数据集包含对象的个数。该算法在数据集的维数增加时具有较好的扩展性,但是时间复杂度的估算仅考虑了搜索时间,而构造索引的任务本身就需要密集复杂的计算量。
3.2、基于密度的度量
基于密度的算法主要有局部离群因子(LocalOutlierFactor,LOF),以及LOCI、CLOF等基于LOF的改进算法。下面我们以LOF为例来进行详细的介绍和实践。
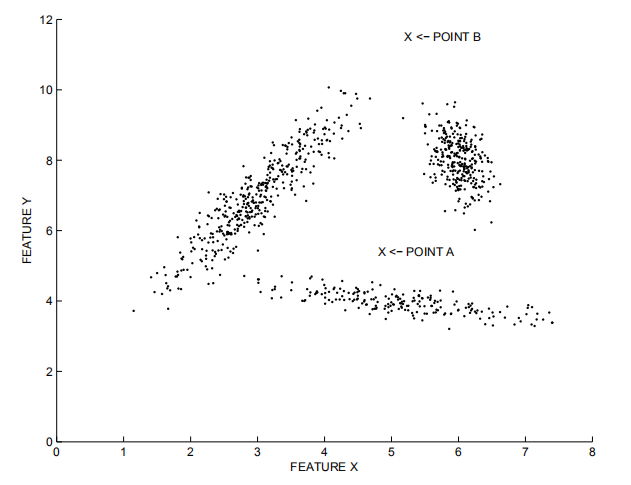
基于距离的检测适用于各个集群的密度较为均匀的情况。在下图中,离群点B容易被检出,而若要检测出较为接近集群的离群点A,则可能会将一些集群边缘的点当作离群点丢弃。而LOF等基于密度的算法则可以较好地适应密度不同的集群情况。
那么,这个基于密度的度量值是怎么得来的呢?还是要从距离的计算开始。类似k近邻的思路,首先我们也需要来定义一个“k-距离”。
3.2.1 k-距离(k-distance(p)):
对于数据集$D$中的给定对象$p$,对象$p$与数据集$D$中任意点$o$的距离为$d(p,o)$。我们把数据集$D$中与对象$p$距离最近的$k$个相邻点的最远距离表示为$k-distance(p)$,把距离对象$p$距离第$k$近的点表示为$o_k$,那么给定对象$p$和点$o_k$之间的距离$d(p,o_k)=k − d i s t a n c e ( p )$,满足:
- 在集合$D$中至少有不包括$p$在内的$k$个点 $o'$,其中$o'∈D{p}$,满足$d(p,o')≤d(p,o_k)$
- 在集合$D$中最多有不包括$p$在内的$k-1$个点$o'$,其中$o'∈D{p}$,满足$d(p,o')<d(p,o_k)$
直观一些理解,就是以对象$p$为中心,对数据集$D$中的所有点到$p$的距离进行排序,距离对象$p$第$k$近的点$o_k$与$p$之间的距离就是k-距离。
3.2.2 k-邻域(k-distance neighborhood):
由k-距离,我们扩展到一个点的集合——到对象$p$的距离小于等于k-距离的所有点的集合,我们称之为k-邻域:$N_{k − d i s t a n c e ( p )}( p ) = { q ∈ D \backslash{ p } ∣ d ( p , q ) ≤ k − d i s t a n c e ( p )}
$。
-
k-邻域包含对象$p$的第$k$距离以内的所有点,包括第$k$距离点。
-
对象$p$的第$k$邻域点的个数$ ∣ N_k(p)∣ ≥ k$。
在二维平面上展示出来的话,对象$p$的k-邻域实际上就是以对象$p$为圆心、k-距离为半径围成的圆形区域。就是说,k-邻域已经从“距离”这个概念延伸到“空间”了。
3.2.3 可达距离(reachability distance):
有了邻域的概念,我们可以按照到对象$o$的距离远近,将数据集$D$内的点按照到$o$的距离分为两类:
- 若$p_i$在对象$o$的k-邻域内,则可达距离就是给定点$p_i$关于对象o的k-距离;
- 若$p_i$在对象$o$的k-邻域外,则可达距离就是给定点$p_i$关于对象o的实际距离。
给定点$p_i$关于对象$o$的可达距离用数学公式可以表示为:
$$r e a c h−d i s t_ k ( p , o ) = m a x {k−distance( o ) , d ( p , o )}$$ 。
这样的分类处理可以简化后续的计算,同时让得到的数值区分度更高。
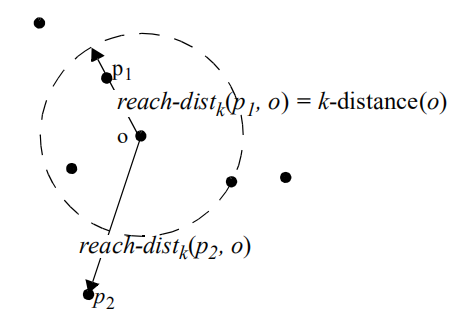
-
$p_1$在对象$o$的k-邻域内,$d ( p_1 , o )<k−distance( o )$,
可达距离$r e a c h−d i s t_ k ( p_1 , o ) = k−distance( o )$ ;
-
$p_2$在对象$o$的k-邻域外,$d ( p_2 , o )>k−distance( o )$,
可达距离$r e a c h−d i s t_ k ( p_2 , o ) = d ( p_2 , o )$ ;
注意:这里用的是$p_k$与$o$的距离$d(p_k,o)$与$o$的k-距离$k−distance( o )$来进行比较,不是与$k−distance( p )$进行比较!
可达距离的设计是为了减少距离的计算开销,$o$的k-邻域内的所有对象$p$的k-距离计算量可以被显著降低,相当于使用一个阈值把需要计算的部分“截断”了。这种“截断”对计算量的降低效果可以通过参数$k$来控制,$k$的值越高,无需计算的邻近点越多,计算开销越小。但是另一方面,$k$的值变高,可能意味着可达距离变远,对集群点和离群点的区分度可能变低。因此,如何选择$k$值,是LOF算法能否达到效率与效果平衡的重要因素。
3.2.4 局部可达密度(local reachability density):
我们可以将“密度”直观地理解为点的聚集程度,就是说,点与点之间距离越短,则密度越大。在这里,我们使用数据集$D$中对象$p$与对象$o$的k-邻域内所有点的可达距离平均值的倒数(注意,不是导数)来定义局部可达密度。
在进行局部可达密度的计算的时候,我们需要避免数据集内所有数据落在同一点上,即所有可达距离之和为0的情况:此时局部密度为∞,后续计算将无法进行。LOF算法中针对这一问题进行了如下的定义:对于数据集$D$内的给定对象$p$,存在至少$MinPts(p)\geq1$个不同于$p$的点。因此,我们使用对象$p$到$o∈N_{MinPts}(p)$的可达距离$reach-dist_{MinPts}(p, o)$作为度量对象$p$邻域的密度的值。
给定点p的局部可达密度计算公式为:$$lrd_{MinPts}(p)=1/(\frac {\sum\limits_{o∈N_{MinPts}(p)} reach-dist_{MinPts}(p,o)} {\left\vert N_{MinPts}(p) \right\vert})$$
由公式可以看出,这里是对给定点p进行度量,计算其邻域内的所有对象o到给定点p的可达距离平均值。给定点p的局部可达密度越高,越可能与其邻域内的点 属于同一簇;密度越低,越可能是离群点。
3.2.5 局部异常因子:
得到lrd(局部可达密度)以后就可以将每个点的lrd将与它们的k个邻点的lrd进行比较,得到局部异常因子LOF。更具体地说,LOF在数学上是对象$p$的邻居点$o$($o∈N_{MinPts}(p)$)的lrd平均值与$p$的lrd的比值。
不难看出,$p$的局部可达密度越低,且它的$MinPts$近邻的平均局部可达密度越高,则$p$的LOF值越高。
如果这个比值越接近1,说明o的邻域点密度差不多,o可能和邻域同属一簇;如果这个比值小于1,说明o的密度高于其邻域点密度,o为密集点;如果这个比值大于1,说明o的密度小于其邻域点密度,o可能是异常点。
由公式计算出的LOF数值,就是我们所需要的离群点分数。
- 参考资料
[1]《Outlier Analysis》——Charu C. Aggarwal
[2] LOF: Identifying Density-Based Local Outliers
更多优质内容请关注公号:汀丶人工智能;会提供一些相关的资源和优质文章,免费获取阅读。

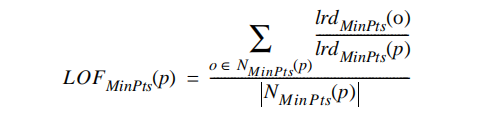


 浙公网安备 33010602011771号
浙公网安备 33010602011771号