原本我也是学习如何将正则表达式一步步化到DFA，搜索发现很多不是死板的定义，就是跨度太大，所以我决定用一道例题，看看它是如何转化的，本次以正则表达式：(a|b)*(aa|bb)(a|b)* 为例。
我看到和多人会介绍将正则表达式转化为NFA的规则，为了便于理解我也选择简单说一下，正则表达式转化为NFA会有基本的一个开始，一个结束，结束为双圈，其余的都是单圈。圆圈里的是状态，圈到圈的线上代表的一个状态到另一个状态的转化条件。对于一个识别空字符的NFA便是：
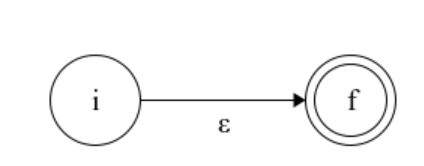
它不需要识别任何字符便可以从开始状态转化为终结状态。所有从开始状态最从转化为终结状态的线路上的字符串的集合便是这个NFA和正则表达式所表示字符串集合。简单的对于一个终结符a：
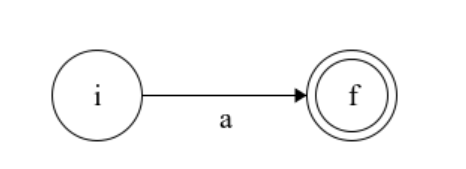
假如我们现在有两个NFA，一个表示识别字符s，记为 N(S); 一个识别字符t，记为 N(T)。那么我们如何表示一个识别字符串 st 的NFA呢？它的规则是将两个NFA连接，只保留一个初始状态，一个终结状态。
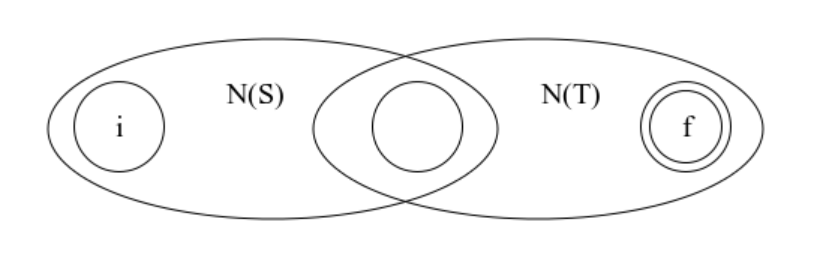
如何表示识别字符 s 或者字符 t 的NFA呢？
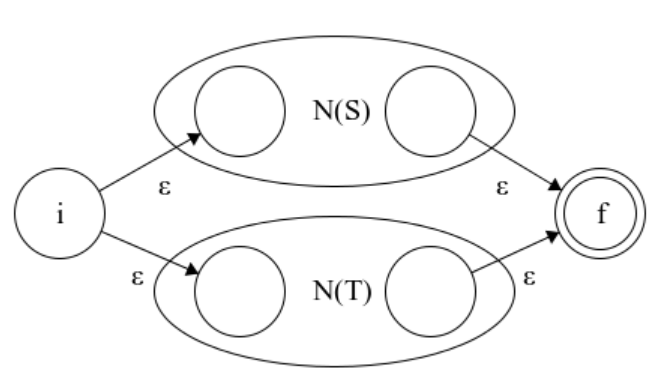
很容易理解，无论选择哪条路，都可以从初始状态转化为终结状态，所以这个NFA可以识别 N(S) 或者 N(T) 能够识别的字符串集合。现在我们继续想一下如何识别n个字符 s 呢？我们可以将N(S)的首尾相连，这样就会循环一次或多次，就可以识别一个或者多个字符 s ，那么零个的情况呢？我们可以直接将 N(S) 的前后相连，这样便也可以选择直接跳过 N(S) 了，如下图所示：
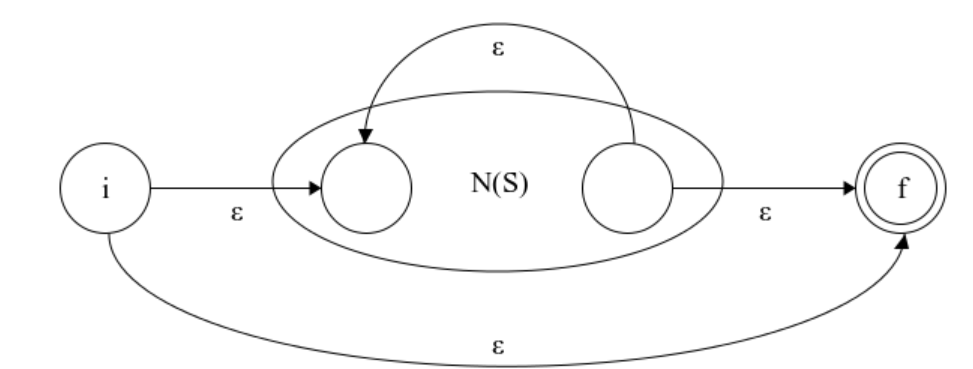
上面便是基本的构建NFA的规则，下面给出几个基本的例子：
对于 a|b：
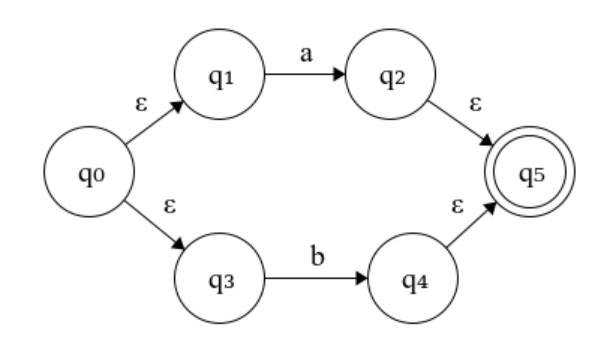
对于 (a|b)*：
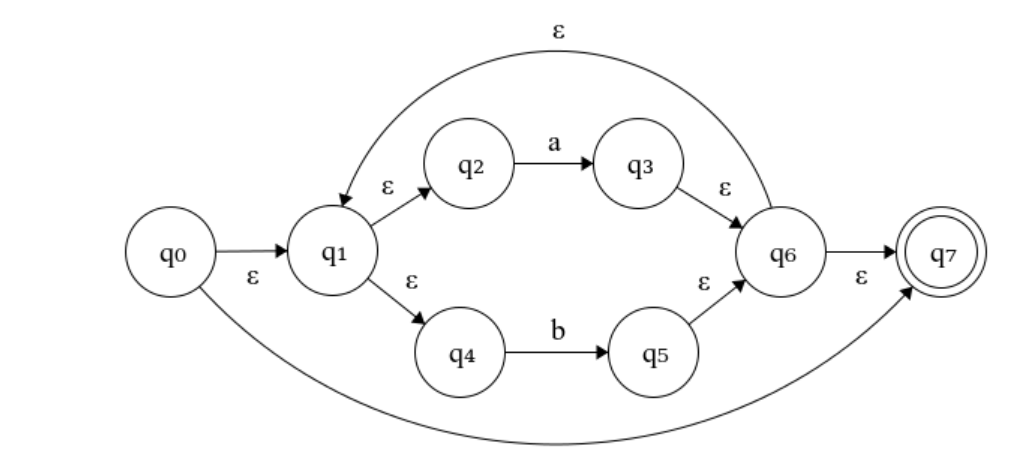
对于(a|b)*c:
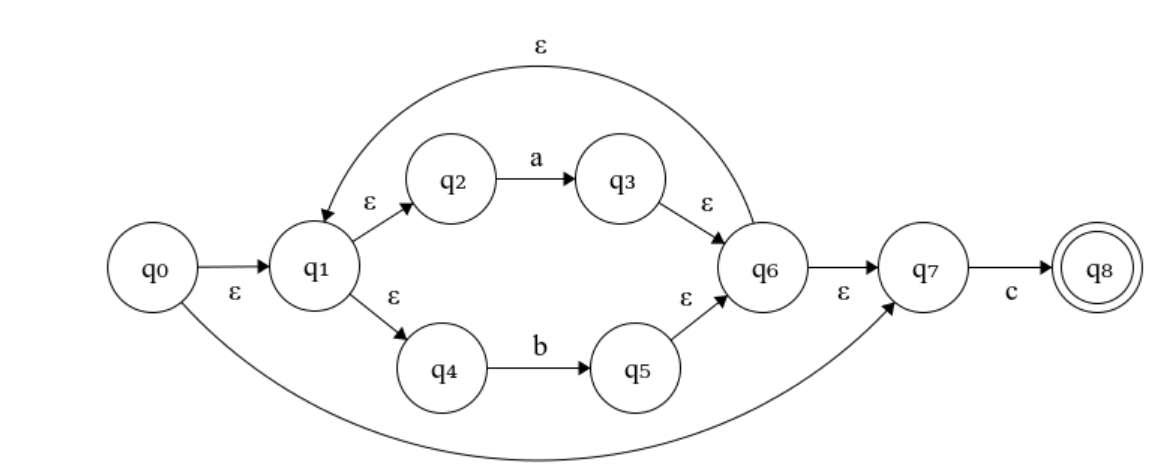
其实在自己做题的时候不需要一步步画这么麻烦的图，上面这么多 ‘空’，看着就让人头大了。下面以(a|b)*(aa|bb)(a|b)* 为例，根据正则表达式画出稍微看着简单的nfa图：
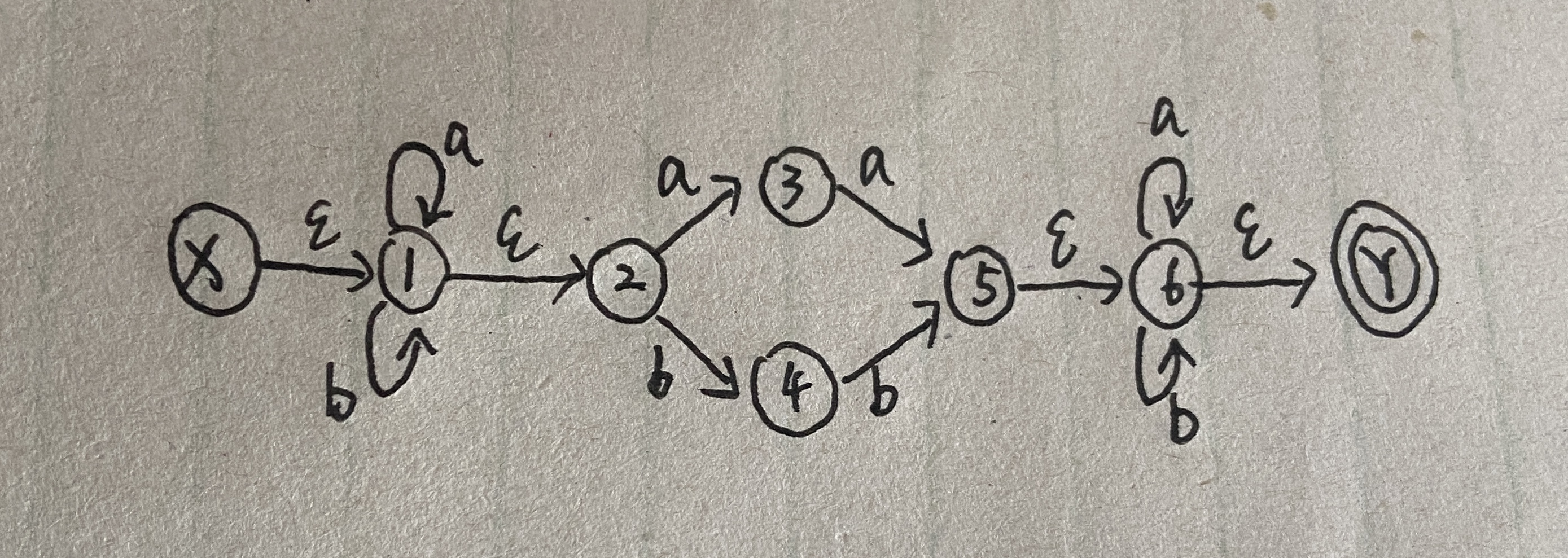
根据的规则是从正则表达式开头开始，遇到 ' * '就先画一个圈，前后两个空，根据 ’ * ‘包含的内容在这个圈的周围继续画圈和线。而中间的连接什么的就不用要 ’空‘ 了。再举一个例子 (a*b)*a*:
现在继续以(a|b)*(aa|bb)(a|b)* 为例，已经转化为 nfa，如何转化为 dfa呢？这里我们使用子集法，我们先给出结果，然后再分析过程是怎样的。
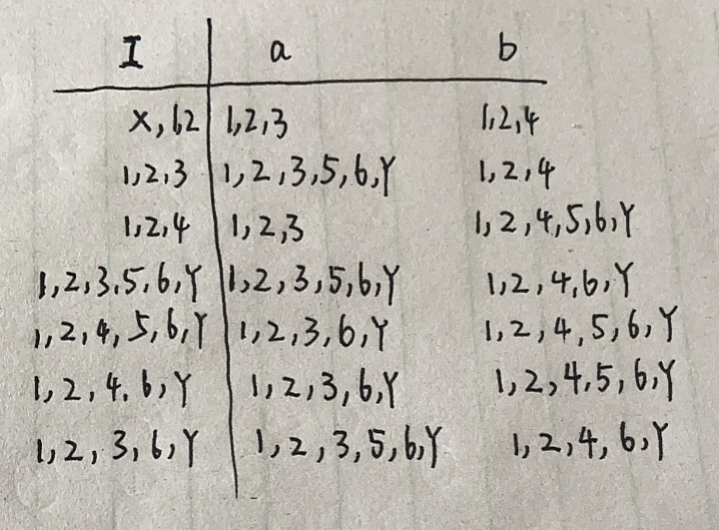
左边是开始的集合元素，右边是先经过a或者b之后可以经过n个 ’空‘ 到达的元素集合。第一个开始的元素集合是X只经过 ’空‘可以到达的元素，由上面的图我们可以知道X只经过 ’空‘ 可以到达1，2. 所以一开始为：X，1，2；
X不能经过a|b
1经过a再经过n个’空‘可以到达：1，2
2经过a再经过n个’空‘可以到达：3
1经过b再经过n个’空‘可以到达：1，2
2经过a再经过n个’空‘可以到达：4
所以左边在经过a|b后得到的右边分别为：{1，2，3} ； { 1，2，4}
接下来左边的元素集合为右边出现的顺序的元素集合，即{1，2，3}；{1，2，4}；.......,需要注意的是，当右边出现 ’空‘，左边也得出现 ’空‘，且’空‘在任何条件下得到的都是’空‘，不能把这一行省略不写。现在我们要为上面的元素集合改改名字：
------------------>>> 
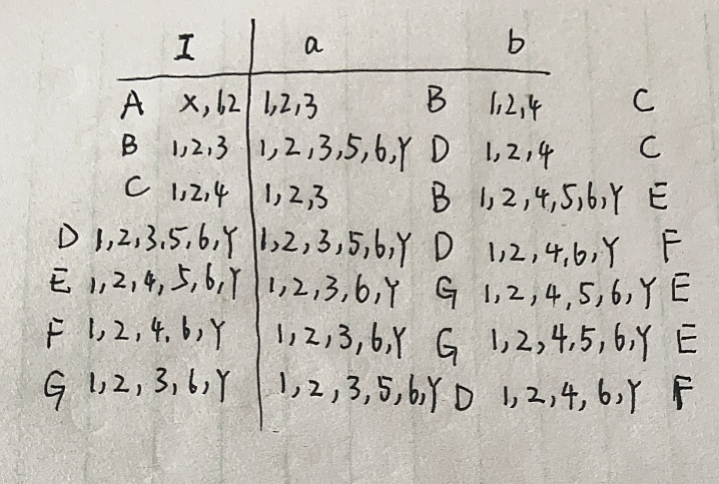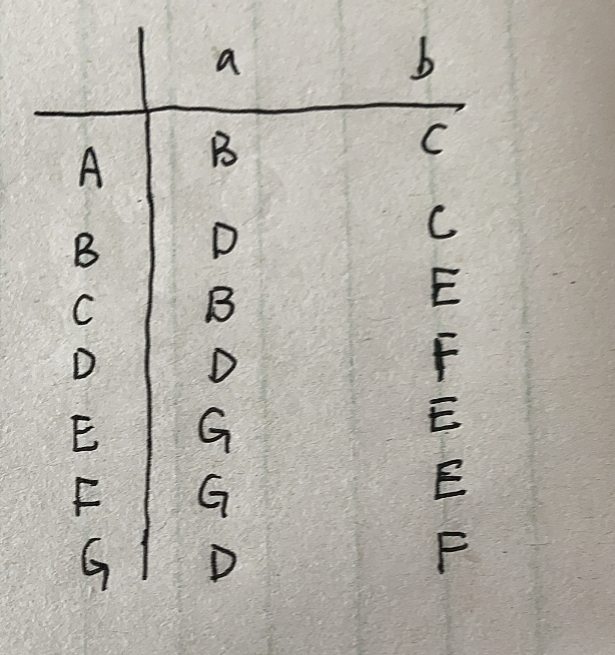
根据上面的图我们可以就画出dfa了：
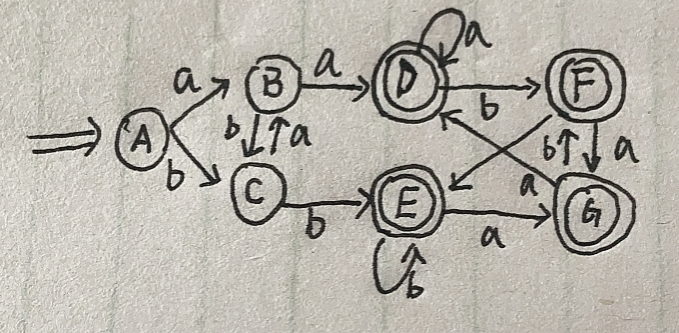
我们可以看到上面的圈中有一个的，也有两个的，前面我们说过两个代表终态，那么如何确定应该是一个还是两个？我们可以看改名字的那张图，在nfa中，Y是终态，此时在dfa中，只要包含Y的就是两个圈，所以D，E，F，G都是两个圈。接下来就该简化我们得到的dfa了，简化的第一步是先将上面的状态分为两类，一个圈的和两个圈的：{A,B,C},{D,E,F,G}，我们用{A,B,C}a={B,D}表示：{A,B,C}在a的条件下可以得到{B,D},则：
{A,B,C}a={B,D}，{B,D}不是{A,B,C}或者{D,E,F,G}的子集，所以要把B分出来{A,C},{B},{D,E,F,G}
{A,C}a={B}是{B}的子集，{A,C}b={C,E}不是{A,C},{B},{D,E,F,G}其中某一个子集，要把C分出来{A},{C},{B},{D,E,F,G}
{D,E,F,G}a={D,G},是{D,E,F,G}的子集，不用分；{D,E,F,G}b={E,F},是{D,E,F,G}的子集，不用分
所以{D,E,F,G}四个可以合成一个D：
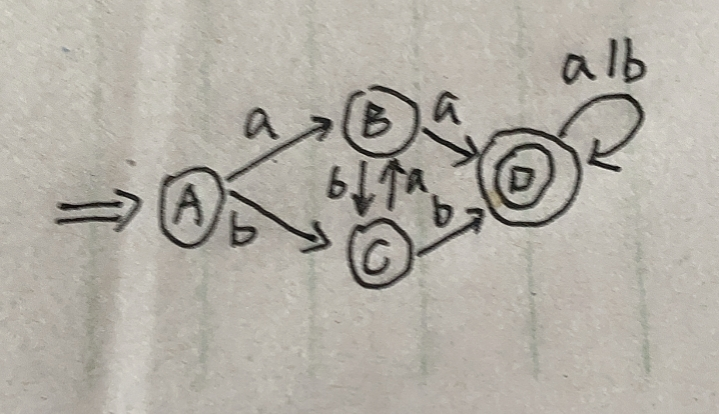
上面就是化简后的dfa，到这里我们就算正则表达式->nfa->dfa->化简的dfa 就结束了。
