In the previous part we have learned how to parse(recognize) and interpreter arithmetic expressions with any any numbers of plus or minus operators in them,for example:3 + 5 -1 + 2. Today we are going to use a more general method to do the same thing, except for replacing addition and subtraction with multiplication and division.And now we will talk quite a bit about another wildely uesd notation for specifying the syntax of a programing language.It's called context-free grammars(grammars,for short) or BNF(Backus-Naur form).In this part,we will not use a pure BNF notation but more like a modified EBNF notation.
Here is a grammar that describes arithmetic expressions like"7 * 4 / 2 * 3"(It's just one of the many expressions that can be generated by the grammar.):
expr : factor( ( MUL | DIV) factor) *
factor: INTEGER
A grammar consists of a sequence of rules,as known as productions.We can easisy see from the above that there are two rules in our grammar.For a rule,the one on the left is a non-terminal which is called the head or left-hand side and the right,called the body or right-hand side,of a colon consists of a sequence of terminals and/or non-terminals .In our rules,tokens like MUL, DIV, INTEGER are called terminals and variables like expr and factor are called non-terminals.
The non-terminal symbol in the first rule is called start symbol which is expr in our example.We can read the rule expr as "An expr can be a factor optionally followed by a multiplication or division operator followed by another factor and so on and so forth."
A grammar defines a language by explianing what sentences it can form.This is how we can derive your arithmetic expression using the grammar:first we begin with the start symbol expr and repeatedly replace a non-terminal by a body of a rule for that non-terminal until you have gengerated a sentence that only consists of terminals.Those sentences form a language defined by the grammar.
If the grammar can not derive a certain arithmetic expression,then it doesn't support that expression and the parser will gengerate a syntax error when it tries to recognize the expression.This is how the grammar derives the expression 3 * 7:
expr -> factor( ( MUL | DIV) factor) * -> factor MUL factor -> INTEGER MUL INTEGER -> 3 * 7
And this is how the grammar derives the expression:3 * 7 / 2:
expr -> factor( ( MUL | DIV) factor) * ->factor MUL factor( ( MUL | DIV) factor) * -> factor MUL factor DIV factor -> INTEGER MUL INTEGER DIV INTEGER ->
3 * 7 / 2
Now,we need map the grammar to code.Here are the guidelines that we will use to convert the grammar to surce code.By following them,We can literally translate the grammar to a working parser:
1. Every rule becomes a method.
2. Alternatives (a1|a2|aN) become an if-elif-else statement.
3.An optional grouping (...)* becomes a whle statement that can loop zero or more times.
4. Each token reference T becomes a call to the method eat. eat(T).
So now we can get a modified expr method like this:
def expr(self): self.factor() while self.current_token.type in (MUL, DIV): token = self.current_token if token.type == MUL: self.eat(MUL) self.factor() elif token.type == DIV: self.eat(DIV) self.factor()
And a syntax diagram for the same expr rule will look:
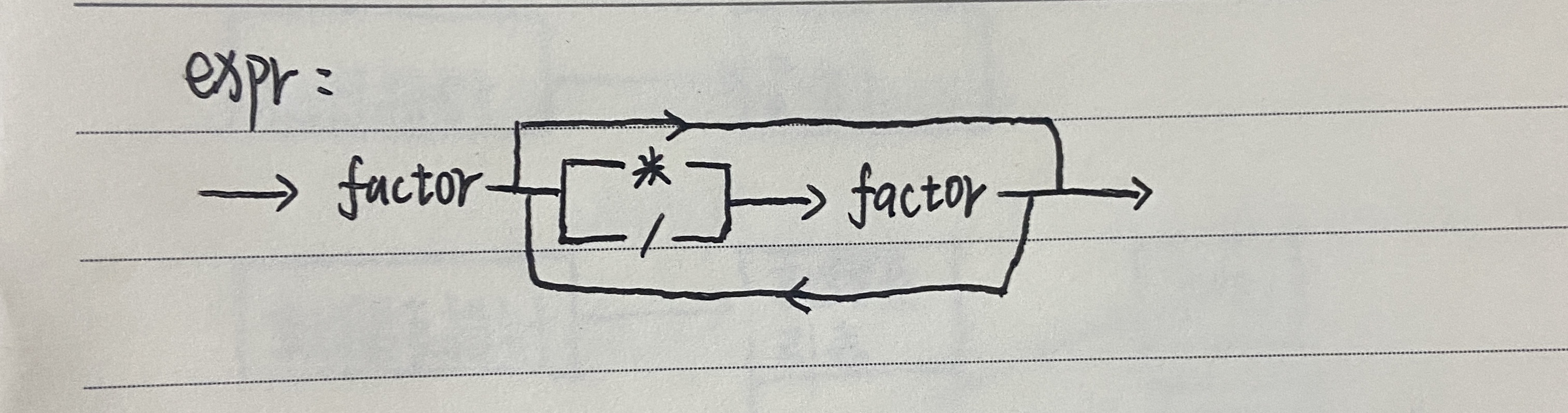
Below is the code of a calculator that can handle valid arithmetic expression containing integers and any number of multiplication and division operators:

# Token types # # EOF (end-of-file) token is used to indicate that # there is no more input left for lexical analysis INTEGER, MUL, DIV, EOF = 'INTEGER', 'MUL', 'DIV', 'EOF' class Token(object): def __init__(self, type, value): # token type: INTEGER, MUL, DIV, or EOF self.type = type # token value: non-negative integer value, '*', '/', or None self.value = value def __str__(self): """String representation of the class instance. Examples: Token(INTEGER, 3) Token(MUL, '*') """ return 'Token({type}, {value})'.format( type=self.type, value=repr(self.value) ) def __repr__(self): return self.__str__() class Lexer(object): def __init__(self, text): # client string input, e.g. "3 * 5", "12 / 3 * 4", etc self.text = text # self.pos is an index into self.text self.pos = 0 self.current_char = self.text[self.pos] def error(self): raise Exception('Invalid character') def advance(self): """Advance the `pos` pointer and set the `current_char` variable.""" self.pos += 1 if self.pos > len(self.text) - 1: self.current_char = None # Indicates end of input else: self.current_char = self.text[self.pos] def skip_whitespace(self): while self.current_char is not None and self.current_char.isspace(): self.advance() def integer(self): """Return a (multidigit) integer consumed from the input.""" result = '' while self.current_char is not None and self.current_char.isdigit(): result += self.current_char self.advance() return int(result) def get_next_token(self): """Lexical analyzer (also known as scanner or tokenizer) This method is responsible for breaking a sentence apart into tokens. One token at a time. """ while self.current_char is not None: if self.current_char.isspace(): self.skip_whitespace() continue if self.current_char.isdigit(): return Token(INTEGER, self.integer()) if self.current_char == '*': self.advance() return Token(MUL, '*') if self.current_char == '/': self.advance() return Token(DIV, '/') self.error() return Token(EOF, None) class Interpreter(object): def __init__(self, lexer): self.lexer = lexer # set current token to the first token taken from the input self.current_token = self.lexer.get_next_token() def error(self): raise Exception('Invalid syntax') def eat(self, token_type): # compare the current token type with the passed token # type and if they match then "eat" the current token # and assign the next token to the self.current_token, # otherwise raise an exception. if self.current_token.type == token_type: self.current_token = self.lexer.get_next_token() else: self.error() def factor(self): """Return an INTEGER token value. factor : INTEGER """ token = self.current_token self.eat(INTEGER) return token.value def expr(self): """Arithmetic expression parser / interpreter. expr : factor ((MUL | DIV) factor)* factor : INTEGER """ result = self.factor() while self.current_token.type in (MUL, DIV): token = self.current_token if token.type == MUL: self.eat(MUL) result = result * self.factor() elif token.type == DIV: self.eat(DIV) result = result / self.factor() return result def main(): while True: try: # To run under Python3 replace 'raw_input' call # with 'input' text = raw_input('calc> ') except EOFError: break if not text: continue lexer = Lexer(text) interpreter = Interpreter(lexer) result = interpreter.expr() print(result) if __name__ == '__main__': main()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号