LDA 资料整理

LDA 中文名叫 隐含狄利克雷分布

有一个讲的数学八卦的pdf，如下：

http://pan.baidu.com/s/1bnX6Pgb

Latent Dirichlet Allocation(LDA)模型是近年来提出的一种具有文本主题表示能力的非监督学习模型。

关键在于：将文档看做是一组主题的混合，词有分配到每个主题的概率。

Probabilistic latent semantic analysis（PLSA） LDA可以看成是服 从贝叶斯分布的PLSA

这篇文章入门比较好：http://blog.csdn.net/huagong_adu/article/details/7937616

 

LDA是一种典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

使用吉布斯采样估计LDA参数

在LDA最初提出的时候，人们使用EM算法进行求解，后来人们普遍开始使用较为简单的Gibbs Sampling，具体过程如下：

• 首先对所有文档中的所有词遍历一遍，为其都随机分配一个主题，即z_m,n=k~Mult(1/K),其中m表示第m篇文档，n表示文档中的第n个词，k表示主题，K表示主题的总数，之后将对应的n^(k)_m+1, n_m+1, n^(t)_k+1, n_k+1, 他们分别表示在m文档中k主题出现的次数，m文档中主题数量的和，k主题对应的t词的次数，k主题对应的总词数。
• 之后对下述操作进行重复迭代。
• 对所有文档中的所有词进行遍历，假如当前文档m的词t对应主题为k，则n^(k)_m-1, n_m-1, n^(t)_k-1, n_k-1, 即先拿出当前词，之后根据LDA中topic sample的概率分布sample出新的主题，在对应的n^(k)_m, n_m, n^(t)_k, n_k上分别+1。

∝

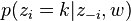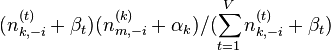
• 迭代完成后输出主题-词参数矩阵φ和文档-主题矩阵θ

 

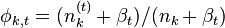
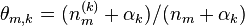
未完待续