https://www.maplesoft.com/products/maple/
Maple高级应用和经典实例: https://wenku.baidu.com/view/f24696210722192e4536f65d.html
Maple高级应用和经典实例: http://vdisk.weibo.com/s/dbLrQxb6KthZA
强大的求解器
几大数学软件各有什么优缺点?
某种程度上这几个软件都用过。但是,MathCAD貌似我只用过几天,而Maple用过几个月吧,这都是约5年前的事情。现在主要用MATLAB和Mathematica。所以以下我讨论一下后两者,简称ML和MM吧。
首先,ML是一种数值计算程序,而MM(及Maple等)是一种符号计算程序。这样来说,两类程序恐怕可比性并不很高。
然后,ML的语言是结构化的、解释性的,MM的语言有点像lisp(看了MM全书以后感触挺深)。这应该是二者的本质区别。相应的优点、缺点,也几乎就是结构化语言和函数型语言的优点、缺点。顺带一提,ML语言为解释性的,其计算效率并不高。
最后,从应用领域的角度看,二者都可谓包罗万象。控制仿真、图像处理、信号分析等等都是ML的强项。它的优势在于工具包非常全面(这弥补了计算效率上的劣势)。MM的我研究得不是很深,但我大略扫过它的文档,感觉功能的数量不亚于ML(对了,MM的数据可视化强于ML;我做过MCM,当时特意用MM显示数据)。
我现在用ML,主要做些数据处理;用MM,主要推些公式。
要补充的是,ML也带有符号计算的功能,但是借用的MuPAD内核(以前貌似是Maple的);而MM也能作数值计算,而且能计算到任意精确的程度。但我认为这些都不是两者的核心功能。参考linux的观点,各个软件将某一方面的能力提升到极致,最后组合起来,可以非常强大。楼上提到MATLAB脚本字体之类的问题,其实完全可以用其他编辑器编辑脚本,然后用ML调用脚本去跑。ML自带编辑器,对我来说是很奇怪的事情,呵呵。
据个人的使用来说,我用这些软件都差不多有十来年,有些七八年的样子.
请相信专业的,顶尖的,自己的深入体会的.自己的眼光最重要,用事实说话,体会其中的精华,而不是表面
精华要从抽象层面和使用层面,这是软件生存的本质
抽象到极致,实践到极致,带点偏见,就是正见
谁用matlab不是冲着工具箱的话,他只用了1/10
谁用Mathematica和Maple不是用符号计算,那也只用了1/3
谁说Matlab也有符号计算的话,不知道他的符号引擎不是自己的,是第二流的引擎,请绕开
工具没有最好,有时候还有审美方面的需求,比如我就一直纠结在Maple和Mathematica之间
以至于两者都会,事实上我最强的是Matlab,使用最久,到现在估计差不多十年了
这些要看个人,工业界,科研界的评判
我看上面的解说,都是谁谁怎么样,您自己呢,但是体会有些地方感觉不怎么对,以下算作补充:
首先,Maple和Mathematica是以符号计算著称,但是近年来Maple和Mathematica在数值计算上也有长足的发展,总体来说Matlab>Mathematica>Maple,差距在缩小;
就符号计算本身来说,如果做过测试的话,Maple>Mathematica>Matlab(现在matlab用mupad的核心,以前用的maple的),所以严格来说Matlab是没有自己的符号计算的.
而从编程范式方面,Mathematica支持的编程范式是最多,什么函数式,子过程式,递归,面向对象,还有很多.甚至非常完美的支持 List等,语法规则比较严格
Maple语法规则太灵活,入门快,但是要成为高手就有点玄乎,相比mathematica要成为高手容易一些,单从语法上说.
2. 从帮助文档上说,Maple不太规范.
Mathematica的方式我最喜欢
Matlab还不错,现在趋向于和Mathematica同样的写作方式写帮助了
3.从公众交换代码方面,Matlab的file exchange最强大,东西最多
Mathematica的alpha平台以及其他也不错
Maple在这块比较弱了
4.从使用上来说,Matlab最强大的是工具箱,他的控制工具箱是一绝,世界上绝无仅有的东西
而其他工具箱很多也达到top1,2,3的样子,而且新技术融入很快,当年的小波,小波包,信号处理方面
现在的代码生成,代码优化方面,直接生成硬件代码
和硬件代码的半硬件调试基本上也是无人能敌了
Mathematica在国外,尤其美国使用者很多
5.数学的顶尖工具箱方面,可以推荐一下
Maple的张量工具箱等,那是高深啊,还有其他一些Mathematica比不上的
有很多ODE,Mathematica解不出来,Maple可以的
Mathematica的差分方程我是很喜欢的
Mathematica在special function的帮助,分类的帮助,说总共有多少类,多少个公式,一一列出,我泪崩,世界上没有比这更好的了.
6.但是Mathematica的语法真心喜欢,如果你对functional paradigm,list,rules这些感兴趣,你会发现,这真是NB
7.在公众贡献放方面
Mathematica贡献了 wolfram function , math world,以及demo等
Maple软件本身带有物理以及数学的很多知识
总的来说:
Matlab适合工程界,尤其是工具箱,快速代码,还有和第三方软件的很多集成,比如优化工具箱
其中最为明显的第三方就是comsol
Mathematica语法优秀,优秀到几乎带有所有的编程范式
Maple符号计算最强,至少在我的测试下是如此,也出了仿真的Maplesim
三个我都用.可惜我没米,买不起
补充:
现在你基本上不用考虑效率方面的问题了
随着硬件的进步,算法的进步
并行支持,分布式计算支持,多核支持,甚至GPU的深度支持
计算速度慢慢退居次要了
可视化编程方面,Maple和Mathematica都有大大的进步,已经到了智能判断很多东西的程度了
推测你的意图
Matlab根据你的鼠标操作生成代码,也是太厉害了
所以易用性,三者差距在缩小
有人说Matlab的图和编码是分开的,但是他有Notebook模式,很多人没用过
Mathematica有cdf,自然编程方式
Maple和Mathematica基本上差不多了
补充:ref
首先一定要看features,得读十来遍吧
Wolfram Research's Product Line of Technical Software, Technologies, and Services
What is Maple: Product Features
Maple Features
然后他们两家自己互掐,注意Matlab不在掐之列,因为他靠工业工具箱,另外两家根本没法跟他比
Similarities between Mathematica & Maple Are Only Skin Deep
Compare Mathematica to Maple: Features Make the Difference
Why Mathematica
Why Mathematica? Compare Mathematica to Other Technical Computing Tools
Analysis of Wolfram Research's Comparison of Mathematica® and Maple
Analysis of Wolfram Research's Comparison of Mathematica速 and Maple- Maplesoft
从我以前早期的浏览历史,Mathematica先掐的Maple
Maple vs Mathematica
注意这句:
In general Maple is more powerful on solving Integral equations, differential equations and Groebner basis, Mathematica is more powerful for integration, recurrence relations, equation solving and simplification.
先说我的观点,再给一个比较权威的结论。
我用过Matlab和Mathematica,我觉得Mathematica的表达能力要更强一些,并且可以把公式文档和计算过程都很优雅地表达在一个notebook里面,说白了就是可以图文并茂地表达一个复杂的过程。mathematica作为写一个算法的快速原型工具,现在可以很方便地实现任意复杂的算法,也容易生成数据去检验。国内讲mathematica的书比较少,大部分是关于数学实验的,专题性质的不多。国外有一些讲得比较深入的,例如wolfrom写的《mathematica全书》,读这些书不仅能让你熟练使用 mathematica,更多地是拓展你在计算机科学的视野。
Matlab的工具箱非常强大,抢占了大部分理工科的阵地,书也很多,可以说是所有数学软件中最多的了吧,用户群也是最大的,到处都可以见到各类论坛。但是目前大家都是把Matlab作为一个应用的工具,讲的不够深入,深入的是那些背后的数学原理。现在几乎理工科各个类别的算法(专业很高的算法)都可以找到matlab版本的。比如我要做数据分类,就用了别人写的matlab版的最小均方SVM,如果是用Mathematica的话,那就得自己写到崩溃了。
最后一点,我一直觉得Matlab的脚本字体不美观,而且完成一个东西一次要写好几个脚本,所以我更愿意用mathematica。
比较权威的比较:
关于几大数学软件的比较,国内一直争论不休,却不知有个德国人在这方面已经做了很精确的比较。一共60多页的文档,从6个大项100多个小项目进行了详细的比较。几十个表格,数千行代码,而且为了保证同样的算法的代码质量,Mathematica的代码由Wolfram Research的人来写,Matlab代码由MathWorks的人来写。不得不佩服德国人做事的严谨,再想想我们还在这里瞎吹,哎。。。。
Maple 51.13%
Mathematica 71.05%
Matlab 69.58%
详细的比较大家自己去看吧。
http://www.scientificweb.com/ncrunch/ncrunch5.pdf
我这里专门写一下Mathematica的软件引擎(下面全部引自mathematica帮助文档)。、
Mathematica 是当今最复杂的软件系统之一. 它由数百万行 C/C++、Java 和 Mathematica 源代码写成.Mathematica 中的 C 代码实际上是用支持一定的内存管理和面向对象特征的扩展 C 语言写成的. Mathematica 代码使用 Share 和 DumpSave 进行了优化.
在 Mathematica 内核中,不同部分的代码构成大致如下:语言和系统占 30%;数值计算占 20%;代数计算占 20%;图形与内核输出占 30%.
大多数代码是相当密集的和系统化的:实际上是简单过程或表的那些部分使用最少的代码,这是因为这些代码趋向于在较高的层次上编写\[LongDash]\[LongDash]常常直接以 Mathematica 语言编写.
内核中的源代码,对于运行 Mathematica 的所有计算机系统是完全相同的.
然而,对于前端,需要大量专门化的代码来支持不同类型的用户界面环境. 前端包含大约 700,000 行独立于系统的 C++ 源代码,其中大约 200,000 行涉及表达式的格式构造. 这里有 50,000 到 100,000 行的特殊代码,这些代码专门处理每个不同的用户界面环境.
Mathematica 使用客户\[LongDash]\[LongDash]服务器计算模型. 前端和内核通过 MathLink 来连接\[LongDash]\[LongDash]使用同样的系统与其它程序通讯. MathLink 支持多个传输层,包含基于 TCP/IP 的和使用共享内存的.
前端与内核使用三个独立的 MathLink 链接来连接. 一个是用于用户提交的计算. 第二个是用于前端求解 Dynamic 表达式的值. 三是用于内核,以通知前端应该使哪个 Dynamic 对象失效.
在 Mathematica 内核的 C 代码部分,主要通过交换完整的 Mathematica 表达式实现不同部分之间的通信,以此来获得模块性和一致性.
但是应当注意,即使系统的不同部分在源代码层次是相当独立的,它也有许多算法的相互依赖性. 例如,我们可以常常看到使用了大量代数算法的数值函数,或者使用嵌入在不同 Mathematica 函数中的高级数学算法的图形代码.
自从1986年 Mathematica 开始发展以来,平均每年有1千开发人员从事 Mathematica 源代码的创建. 此外,与代码创建相当的精力或者更多的精力用在代码的测试和验证上.
自从第1版发行以来,Mathematica 的源代码已经有了很大改变. 在内核中的代码总行数从第1版的 150,000 行,到第2版的 350,000 行,又到第3版的 600,000 行,第4版的 800,000 行,第5版的一千五百万行,到第6版的两千五百万行. 此外,在每个阶段,现有代码都被修改了\[LongDash]\[LongDash]因此,在第6版中,仅有很少的一部分代码与第1版中的代码是相同的.
然而,尽管在内部代码中有这些变化,Mathematica 用户层次的设计一直保持与第1版的兼容性. 到目前为止,添加了许多新功能,但 Mathematica 第1版中创建的程序无需任何改变,绝对能在第 6 版中运行.
我正好用过其中的3个软件,我回答一下:
(我在PTC工作的时候,正好公司收购MATHCAD,公司做过多次竞争软件评估)
四大数学软件:Maple、MATLAB、MathCAD(被PTC收购)和Mathematica。
1)MATHCAD:如果仅仅是要求一般的计算或者是普通用户日常使用,首选的是MathCAD,它在高等数学方面所具有的能力,足够一般客户的要求,而且它的输入界面也特别友好(类似word界面)。设计院客户比较多,用于写计算说明书。
2)如果要求计算精度、符号计算和编程方面的能力,推荐用Mathematica。
3)如果有实时数据流,仿真方面的运算,推荐MATLAB,它的矩阵计算和图形处理方面则是它的强项。国防/军工/电子行业客户比较多。
4)MAPLE我没有用过。
只有mathematica才有官方中文帮助啊,而且排版非常清爽。
相比起来,其余2者差了远了,而且例子也是mathematica最丰富。
mathematica画出来的图非常好看,
输出的图能和文字、计算、公式放在一起,而不是像matlab单独弹出个窗口。
而且,mathematica输入输出的格式和我们平常使用的格式很接近,
当然目前的maple也是,只有matlab还得用很多括号。。。
从最新版本的占用空间上看,maple只有500MB不到,mathematica有1GB,matlab大概有4GB。
还有点非常无语,matlab每年都会出2个版本……而且版本号非常容易混淆,貌似有段时间是向下降的。
maple和matlab应该主要是用java语言写的,
而mathematica主要是用c语言。不过---->(评论里曹洪洋先生指出这是错的)
我说一个 Julia;
优点:
1. 速度快
2. 有时(其实是经常)可以当做 Lisp 写
3. 可以方便的部分达到 CPP 的 template-based programming 的效果,增强稳健性(防御式编程)和运行速度(型别已知)
4. 随意调用 Python 包
5. 有 best (coding) practice 做参考
6. 暂时我还没有玩过,但是可以用 JuMP 的方法用 macro 写 DSL
1. 虽然对我来说不是缺点,但是每次准备安利时发现没有 IDE 安利不能
2. 自用的包每次更新的时候要调整不少避免 warning
3. 虽然常常有 pre-compiled 的版本,但是不编译一个最新 master 版本会不舒服
4. 偶尔编译时会有蛋疼情况,比如系统上的 llvm 和编译要求的不一样
过去本人从事理论物理研究工作,现在则从事生物、计算机科学研究,使用机器学习工具,本人尝试从个人经验讨论各类软件的优劣。
Mathematica:
长处:算符运算能力强大,界面美观,语言简洁,容易取得真实数据,画图精美
短处:运算速度慢,受界面影响,不利处理大量数据
MATLAB / Octave:
长处:向量化语法,大量工具箱
短处:语言易读性低
Python + NumPy + SciPy:
长处:语言简洁,可做数值计算以外的工作(如网搜数据),大量工具箱
短处:算符运算能力不强且繁冗
长处:大量统计工具箱,可快速处理大量数据,画图精美
短处:功能限于统计方面,语法晦涩
其实数学软件之间是不太好比较的,因为面向的用户群体完全不同,彼此并不太构成竞争。
以 Matlab 为例,一般来说它被看成是最重要的数学软件,可是事实上 Matlab 更象是一个编程环境,而不是一个软件。如果要比较,Matlab 应该和 python 之类做比较更好。和所有其它数学软件相比,Matlab 在编程方面的功能都远远胜出,不在一个水平线上。
Mathematica 才是一个真正意义上的数学软件,或者确切来说,是「计算软件」,是用来算东西的。比如算100的阶乘,比如一个多项式的根,比如画出一条曲线的形状。这些它可以做的非常好,但是也仅限于此。要用它开发出一个新算法是几乎做不到的。所以真正的数学研究或者相关领域的研究反而没人用 mathematica,就像数学家并不真的需要用计算器一样。
Mathcad 其实不是一个数学软件,而是一个「写数学」的软件,可以很方便的输入,但是长处也仅限于此。不过今天在数学公式输入方面,latex 已经是事实上的标准了,所以 mathcad 的市场其实是相当有限的。
Maple 在我印象里是一个没落中的软件。曾经在学术界有很多人喜欢,但是今天似乎已经没什么人在用了。作为计算机数学方向的研究生一枚,Matlab、Maple、Mathematica、MathCAD、maxima、mathμ这些软件我都用过,当前在学术、工业、教育界上较流行和出名的科学计算软件分为两类,主要包含数值计算软件(以MATLAB为代表)和符号计算软件(比如:Mathematica、Maple、Maxima、MathCAD、Reduce等,更多此类软件请访问Computer algebra system - wikipedia)两大类,还有近几年来在中国缓慢发展但尚未推广使用的符号计算软件mathμ。
(1)Maxima,是由麻省理工学院在美国能源部的支持下于60年代末创造的Macsyma演变而来,世界上最早的符号计算系统(或称为计算机代数系统CAS)。Macsyma后来慢慢走上商业化的道路,自1982年开始,Bill Schelter教授默默地维护基于能源部获得的代码的Macsyma,他把这个软件叫做Maxima,开放源码。因为版权的问题,Maxima一直没有公开发行,只有少数人知道有这个软件的存在。1998年,Maxima终于得到公开发行的许可,这已是Schelter教授努力了16年之后的事。Schelter教授在2001年去世,不过已经正式成为合法开放源码软件,因此陆续有支持开放源码的程式设计师,学者投入Maxima的开发工作。Maxima的前身Macsyma在当时是非常创新的软件。现在流行的商业计算机代数系统软件Maple及Mathematica,都是受到Macsyma的启发而设计出来的。
(2)Mathematica是由世界著名物理学家Stephen Wolfram领导的Wolfram Research公司开发的科学计算软件。它兼具强大的符号计算功能和数值处理功能,被称为世界上最强大的通用计算系统。
(3)Maple是由加拿大Waterloo大学开发的科学计算软件,拥有优秀的符号计算和数值计算能力。并且其符号计算同时是MATLAB和MathCAD等软件的符号处理的核心。2009年,Maplesoft被日本软件商Cybernet Systems收购。(About Maplesoft: Maplesoft, a subsidiary of Cybernet Systems Co., Ltd. in Japan, is the leading provider of high-performance software tools for engineering, science, and mathematics. Its product suite reflects the philosophy that given great tools, people can do great things.)
(4)MATLAB是美国MathWorks公司的科学计算软件,具有超强的数值计算功能。使用MATLAB,可以分析数据,开发算法,创建模型和应用程序。MATLAB在信号处理和通信、图像和视频处理、控制系统、测试和测量、计算金融学及计算生物学等众多应用领域已成为科研工作着和大学生进行科学研究的一种强有力工具。
(5)MathCAD是美国PTC公司旗下MathSoft子公司推出的一个交互式的数学软件。MathCAD是集科学编辑、数学计算、和仿真于一体的软件,主要特点是输入界面比较友好,所见即所得。MathCAD可视作一个功能强大的计算器,没有复杂的使用规则;同时它和Word、WPS等文字处理软件配合使用良好。
(6)清华大学的mathμ研发团队的科技发明制作“计算机代数系统mathμ”是一个符号计算软件,mathμ研发团队官方声称mathμ具有独特的符号处理功能,国内领先,但它使用起来依旧需要学习专门的输入语法和命令,此外也尚未推广使用。
从功能上而言,目前科学计算领域的符号计算和数值计算基本已被Mathematica和MATLAB所覆盖。Maple为MATLAB和MathCAD等计算软件的符号计算提供内核,MathCAD主要提供较强的数学表达式编辑的功能。
发现有个地方的回答也还不错:MAXIMA,Mathematica 和 Maple 的区别
GeoGebra
数学老师那些几何图形,什么多边形,各种函数其实都不是自己画的哦
这个软件提供很多模板,就是数学老师绘图必备啊
选择数学软件或者工具、语言的时候,一般考虑两个维度:抽象高度 和 扩展广度。
先从容易理解的说起。所谓扩展广度,也就是说软件的工作能力,比如数据可视化、作图的能力,读取各种数据源的能力(文本,表格,数据库),与其他软件集成、提供接口调用的能力,扩展第三方程序集的能力,以及使用界面是否人性化。但是,如果功能太强大,什么功能都具备,那么软件上手难度会相应的增大,违法了“大道至简”的原则。
再谈抽象高度。所谓抽象高度,也就是这个软件的最基本数据思维逻辑单元是什么。大家熟悉的Matlab,其核心数据结构就是矩阵,一个向量也可以看做一个矩阵。Matlab的一切计算基础都是矩阵运算。抽象程度高的优点有两个:
- 用户可以绕过底层数据逻辑,直接思考实现顶层的算法,跳过琐碎的程序细节;
- 可以大大提升运算速度。为什么Matlab的矩阵运算速度那么快?因为矩阵是其基本数据结构,所以Matlab中核心的矩阵运算是在二进制内存级别上完成的。
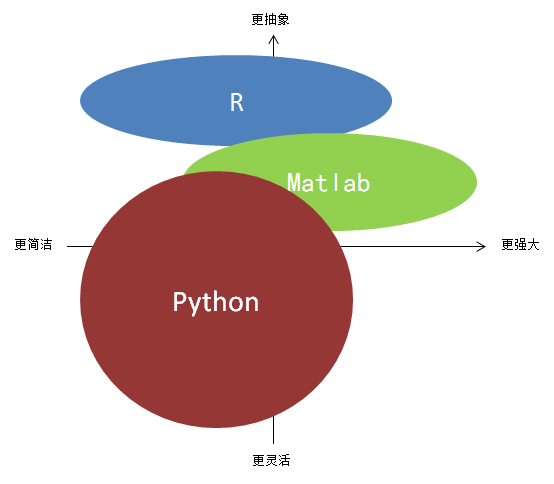
P.S. 这里的Python指扩展了numpy, scipy库。
限于对其他软件的了解有限,所以无法发布意见。。。不过这种分类方法还是可以考虑的,用来寻找适合自己的数学工具。还记得我的第一行代码:
Plot[sin[x], {x, 0, 2 Pi}]debug 花了一个下午......差点就要对它绝望了…
Matlab其实是个工程软件。纯数学方面并不强,符号运算更是渣。但是变成方便,适合做模拟和一般计算工作。当然,因为是脚本语言,所以效率比不上一般的编程语言。它主要胜在适用面非常广,这种库的支持非常好,还有专门输出报表的库。因此,系统模拟,控制系统设计、图像处理、信号处理等等都可以用。我还用这软件来排相框。
MathCAD没有用过,不清楚。Maple感觉纯数学、推公式更适用些,适用面比较窄。Mathematica据说也可以做一些工程应用方面的工作,但是我没有用过这方面的功能,所以无法评论。首先,对于学生来说,如果只是写论文或者做数据处理,他们的区别是不的,基本想实现的功能每一个都能实现。所以,学好一个就够用很久了,当然如果是工作另当别论。
其次,从每个软件的特点来说,个人感觉如下:
stata eviews偏统计计量方面,eviews更适合做时间序列,stata更适合做面板。曾经用stata做过时间序列,但功能不如eviews强大,比如检验稳定性剔除趋势,stata只有默认的线性趋势,eviews可以设置多种趋势。除此外,感觉stata比eviews好用很多,命令非常简单。
r,sas都是很强大的统计软件,现在做大数据这俩用的很多,上面的基本没听到过有谁用。不过个人很喜欢r一点,命令简单,而且是免费的。但是r自带的编译器不太行,需要下别的插件。
matlab功能更综合一些,工程啊,金融啊都能用,比如用他做量化交易策略测试很好用。
尤其是有大量现成的工具包的情况下
Maple (software)

Maple interface
|
|
| Developer(s) | Waterloo Maple (Maplesoft) |
|---|---|
| Initial release | 1982 |
| Stable release |
2016 / March 2, 2016
|
| Written in | C, Java, Maple |
| Platform | Microsoft Windows (7, 8 and 10), Apple OS X, Linux |
| Available in | English, Japanese, and limited support in additional languages[1] |
| Type | Computer algebra system, Numeric computation |
| License | Proprietary commercial software |
| Website | www.maplesoft.com/products/maple/ |
Maple is a symbolic and numeric computing environment, and is also a multi-paradigm programming language.
Developed by Maplesoft, Maple also covers other aspects of technical computing, including visualization, data analysis, matrix computation, and connectivity.
A toolbox, MapleSim, adds functionality for multidomain physical modeling and code generation.
Overview[edit]
Core functionality[edit]
Users can enter mathematics in traditional mathematical notation. Custom user interfaces can also be created. There is support for numeric computations, to arbitrary precision, as well as symbolic computation and visualization. Examples of symbolic computations are given below.
Maple incorporates a dynamically typed imperative-style programming language which resembles Pascal.[2] The language permits variables of lexical scope. There are also interfaces to other languages (C, C#, Fortran, Java, MATLAB, and Visual Basic). There is also an interface to Excel.
Maple supports MathML 2.0, a W3C format for representing and interpreting mathematical expressions, including their display in Web pages.[3]
Architecture[edit]
Maple is based on a small kernel, written in C, which provides the Maple language. Most functionality is provided by libraries, which come from a variety of sources. Most of the libraries are written in the Maple language; these have viewable source code. Many numerical computations are performed by the NAG Numerical Libraries, ATLAS libraries, or GMP libraries.
Different functionality in Maple requires numerical data in different formats. Symbolic expressions are stored in memory as directed acyclic graphs. The standard interface and calculator interface are written in Java.
History[edit]
The first concept of Maple arose from a meeting in November 1980 at the University of Waterloo. Researchers at the university wished to purchase a computer powerful enough to run Macsyma. Instead, it was decided that they would develop their own computer algebra system that would be able to run on lower cost computers. The first limited version appearing in December 1980 with Maple demonstrated first at conferences beginning in 1982. The name is a reference to Maple's Canadian heritage. By the end of 1983, over 50 universities had copies of Maple installed on their machines.
In 1984, the research group arranged with Watcom Products Inc to license and distribute the first commercially available version, Maple 3.3.[4] In 1988 Waterloo Maple Inc. was founded. The company’s original goal was to manage the distribution of the software. Eventually, the company evolved to have an R&D department where most of Maple's development is done today with the rest done at university research labs worldwide including: the Symbolic Computation Laboratory at the University of Waterloo and the Ontario Research Centre for Computer Algebra at the University of Western Ontario[who?].
In 1989, the first graphical user interface for Maple was developed and included with version 4.3 for the Macintosh. X11 and Windows versions of the new interface followed in 1990 with Maple V. In 1992, Maple V Release 2 introduced the Maple "worksheet" that combined text, graphics, and input and typeset output.[5] In 1994 a special issue of a newsletter created by Maple developers called MapleTech was published.[6]
In 1999, with the release of Maple 6, Maple included some of the NAG Numerical Libraries.[7] In 2003, the current "standard" interface was introduced with Maple 9. This interface is primarily written in Java (although portions, such as the rules for typesetting mathematical formulae, are written in the Maple language). The Java interface was criticized for being slow;[8] improvements have been made in later versions, although the Maple 11 documentation[9] recommends the previous (“classic”) interface for users with less than 500 MB of physical memory.
Between the mid 1995 and 2005 Maple lost significant market share to competitors due to a weaker user interface.[10] In 2005, Maple 10 introduced a new “document mode”, as part of the standard interface that it has been further developed over the following years.
In September 2009 Maple and Maplesoft were acquired by the Japanese software retailer Cybernet Systems.
Features[edit]
Features of Maple include:[11]
- Support for symbolic and numeric computation with arbitrary precision
- Elementary and Special mathematical function libraries
- Complex numbers and interval arithmetic
- Arithmetic, greatest common divisors and factorization for multivariate polynomials over the rationals, finite fields, algebraic number fields, and function fields
- Limits, series and asymptotic expansions
- Groebner bases
- Differential Algebra
- Matrix manipulation tools including support for sparse arrays
- Mathematical function graphing and animation tools
- Solvers for systems of equations, diophantine equations, ODEs, PDEs, DAEs, DDEs and recurrence relations
- Numeric and symbolic tools for discrete and continuous calculus including definite and indefinite integration, definite and indefinite summation, automatic differentiation and continuous and discrete integral transforms
- Constrained and unconstrained local and global optimization
- Statistics including model fitting, hypothesis testing, and probability distributions
- Tools for data manipulation, visualization and analysis
- Tools for probability and combinatoric problems
- Support for time-series and unit based data
- Connection to online collection of financial and economic data
- Tools for financial calculations including bonds, annuities, derivatives, options etc.
- Calculations and simulations on random processes
- Tools for text mining including regular expressions
- Tools for signal processing and linear and non-linear Control systems
- Discrete math tools including number theory
- Tools for visualizing and analysing directed and undirected graphs
- Group theory including permutation and finitely presented groups
- Symbolic tensor functions
- Import and export filters for data, image, sound, CAD, and document formats
- Technical word processing including formula editing
- Programming language supporting procedural, functional and object-oriented constructs
- Tools for adding user interfaces to calculations and applications
- Tools for connecting to SQL, Java, .NET, C++, Fortran and http
- Tools for generating code for C, C#, Fortran, Java, JavaScript, Julia, Matlab, Perl, Python, R, and Visual Basic
- Tools for parallel programming
Examples of Maple code[edit]
Sample imperative programming constructs:
myfac := proc(n::nonnegint)
local out, i;
out := 1;
for i from 2 to n do
out := out * i
end do;
out
end proc;
Simple functions can also be defined using the "maps to" arrow notation:
myfac := n -> product( i, i=1..n );
Integration[edit]
Find
- {\displaystyle \int \cos \left({\frac {x}{a}}\right)dx}
.
int(cos(x/a), x);
Answer:
- {\displaystyle a\sin \left({\frac {x}{a}}\right)}
Determinant[edit]
Compute the determinant of a matrix.
M:= Matrix([[1,2,3], [a,b,c], [x,y,z]]); # example Matrix
- {\displaystyle {\begin{bmatrix}1&2&3\\a&b&c\\x&y&z\end{bmatrix}}}
LinearAlgebra:-Determinant(M);
- {\displaystyle bz-cy+3ay-2az+2xc-3xb}
Series expansion[edit]
series(tanh(x),x=0,15)
- {\displaystyle x-{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}-{\frac {17}{315}}\,x^{7}}
- {\displaystyle +{\frac {62}{2835}}\,x^{9}-{\frac {1382}{155925}}\,x^{11}+{\frac {21844}{6081075}}\,x^{13}+O(x^{15})}
Solve equation numerically[edit]
High order polynomial equation
f := x^53-88*x^5-3*x-5 = 0
fsolve(f)
-1.097486315, -.5226535640, 1.099074017
Solve equation set[edit]
f := (cos(x+y))^2 + exp(x)*y+cot(x-y)+cosh(z+x) = 0:
g := x^5 - 8*y = 2:
h := x+3*y-77*z=55;
fsolve( {f,g,h} );
{x = -1.543352313, y = -1.344549481, z = -.7867142955}
Plotting of function of single variable[edit]
- Plot {\displaystyle x\cdot \sin(x)}
with {\displaystyle x}
ranging from -10 to 10
plot(x*sin(x),x=-10..10);
Plotting of function of two variables[edit]
- Plot {\displaystyle x^{2}+y^{2}}
with {\displaystyle x}
and {\displaystyle y}
ranging from -1 to 1
plot3d(2-x-(y^2-x^2)^0.5), x=0..1, y=0..1);
Animation of functions[edit]
- animation of function of two variables
- {\displaystyle f:=2\cdot k^{2}/\cosh(k\cdot (x-4\cdot k^{2}\cdot t))^{2}}
plots:-animate(subs(k = .5, f), x=-30..30, t=-10..10, numpoints=200, frames=50, color=red, thickness=3);
- animation of functions of three variables
plots:-animate3d(cos(t*x)*sin(3*t*y), x=-Pi..Pi, y=-Pi..Pi, t=1..2);
- Fly-through animation of 3-D plots.[12]
M := Matrix([[400,400,200], [100,100,-400], [1,1,1]], datatype=float[8]): plot3d(1, x=0..2*Pi, y=0..Pi, axes=none, coords=spherical, viewpoint=[path=M]);
Laplace transform[edit]
f := (1+A*t+B*t^2)*exp(c*t);
- {\displaystyle (1+A\cdot t+B\cdot t^{2})\cdot e^{c\cdot t}}
inttrans:-laplace(f, t, s);
- {\displaystyle {\frac {1}{s-c}}+{\frac {A}{(s-c)^{2}}}+{\frac {2B}{(s-c)^{3}}}}
- inverse Laplace transform
inttrans:-invlaplace(1/(s-a),s,x)
- {\displaystyle e^{ax}}
Fourier transform[edit]
inttrans:-fourier(sin(x),x,w)
- {\displaystyle \mathrm {I} \pi \,(\mathrm {Dirac} (w+1)-\mathrm {Dirac} (w-1))}
Integral equations[edit]
Find functions {\displaystyle f}
- {\displaystyle f(x)-3\int _{-1}^{1}(xy+x^{2}y^{2})f(y)dy=h(x)}
.
eqn:= f(x)-3*Int((x*y+x^2*y^2)*f(y), y=-1..1) = h(x):
intsolve(eqn,f(x));
- {\displaystyle f\left(x\right)=\int _{-1}^{1}\!\left(-15\,{x}^{2}{y}^{2}-3\,xy\right)h\left(y\right){dy}+h\left(x\right)}
Use of the Maple engine[edit]
The Maple engine is used within several other products from Maplesoft:
- Maple T.A., Maplesoft’s online testing suite, uses Maple to algorithmically generate questions and grade student responses.
- MapleNet allows users to create JSP pages and Java Applets. MapleNet 12 and above also allow users to upload and work with Maple worksheets containing interactive components.
- MapleSim, an engineering simulation tool.[13]
Listed below are third-party commercial products that no longer use the Maple engine:
- Versions of Mathcad released between 1994 and 2006 included a Maple-derived algebra engine (MKM, aka Mathsoft Kernel Maple), though subsequent versions use MuPAD.
- Symbolic Math Toolbox in MATLAB contained a portion of the Maple 10 engine, but now uses MuPAD (starting with MATLAB R2007b+ release).[14]
- Older versions of the mathematical editor Scientific Workplace included Maple as a computational engine, though current versions include MuPAD.
See also[edit]
- Comparison of computer algebra systems
- Comparison of numerical analysis software
- Comparison of programming languages
- Comparison of statistical packages
- List of graphing software
- List of computer algebra systems
- List of computer simulation software
- List of numerical analysis software
- Mathematical software
- SageMath (an open source algebra program)



 .
.




 with
with  ranging from -10 to 10
ranging from -10 to 10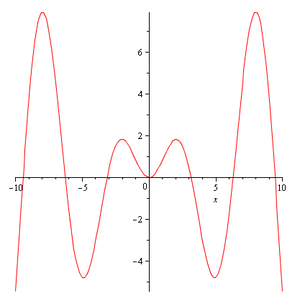
 with
with  ranging from -1 to 1
ranging from -1 to 1








 .
.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号