softmax杂谈

softmax杂谈

在多分类问题中，我们可以使用 softmax 函数，对输出的值归一化为概率值。下面举个例子：

import sys

sys.path.append("E:/zlab/")
from plotnet import plot_net, DynamicShow

num_node_list = [10, 7, 5]
figsize = (15, 6)
plot_net(num_node_list, figsize, 'net')

Press `c` to save figure to "net.svg", `Ctrl+d` to break >>
> c:\programdata\anaconda3\lib\site-packages\viznet\context.py(45)__exit__()
-> plt.savefig(self.filename, dpi=300)
(Pdb) c

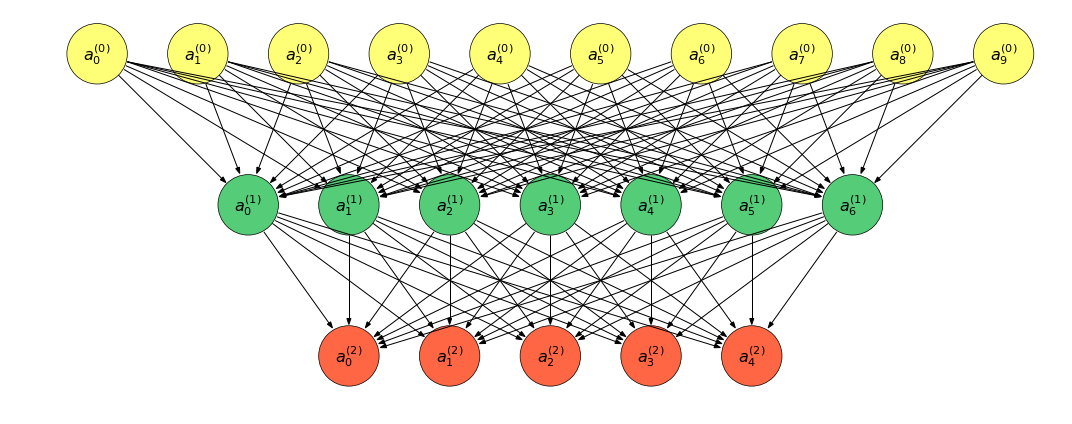
上图转换为表达式：

 

𝑎(0)=(𝑎(0)0,𝑎(0)1,⋯,𝑎(0)9)𝑇𝑎(1)=(𝑎(1)0,𝑎(1)1,⋯,𝑎(1)6)𝑇𝑎(2)=(𝑎(2)0,𝑎(2)1,⋯,𝑎(2)4)𝑇a(0)=(a0(0),a1(0),⋯,a9(0))Ta(1)=(a0(1),a1(1),⋯,a6(1))Ta(2)=(a0(2),a1(2),⋯,a4(2))T

 

对于任意的 0≤𝑖≤20≤i≤2, 有前向传播的表达式：

 

𝑧(𝑖+1)=𝑊(𝑖)𝑎(𝑖)+𝑏(𝑖)𝑎(𝑖+1)=𝑓(𝑖+1)(𝑧(𝑖+1))z(i+1)=W(i)a(i)+b(i)a(i+1)=f(i+1)(z(i+1))

 

其中，𝑓(𝑗)f(j) 表示激活函数，除了输出层外，一般使用 ReLU 函数；𝑊(𝑖),𝑏(𝑖)W(i),b(i) 为模型参数。

如若我们有 𝑚m 个样本 {𝑥(𝑗)}𝑚𝑗=1{x(j)}j=1m 组成的数据集 𝐷D, 称 𝑋=(𝑥(1),𝑥(2),⋯,𝑥(𝑚))𝑇X=(x(1),x(2),⋯,x(m))T 为数据集 𝐷D 的设计矩阵。

这样，前向传播可以改写为：

 

{𝑍(1+𝑖)=𝑍(𝑖)𝑊(0)+(𝑏(𝑖))𝑇𝐴(1+𝑖)=𝑓(1+𝑖)(𝑍(1+𝑖)){Z(1+i)=Z(i)W(0)+(b(i))TA(1+i)=f(1+i)(Z(1+i))

 

• 𝑍(𝑖)=(𝑧(𝑖)1,𝑧(𝑖)2,⋯,𝑧(𝑖)𝑚)𝑇Z(i)=(z1(i),z2(i),⋯,zm(i))T, 这里对 𝑧(𝑖)z(i) 添加下标以区别不同的样本;
• 这里对列向量 𝑏(𝑖)b(i) 进行了 broadcast 操作;
• 且 𝑍(0)=𝑋Z(0)=X.

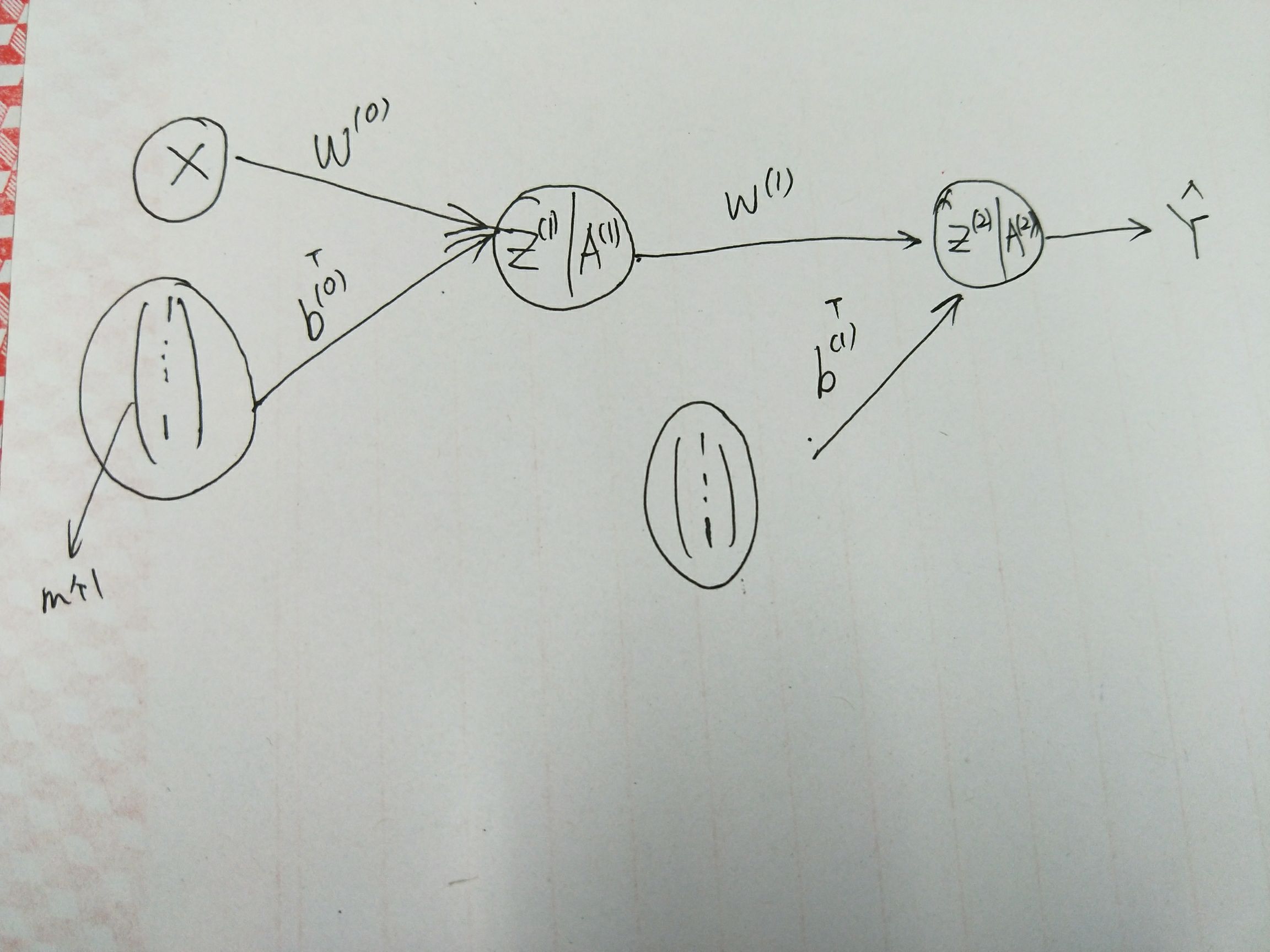
对于多分类问题，一般输出层对应的激活函数的 softmax 函数：

求解 𝐴(2)A(2):

1. 计算 𝑒𝑥𝑝=exp(𝑍(1))exp=exp⁡(Z(1));
2. 对 𝑒𝑥𝑝exp 按列做归一化, 便可得到 softmax(𝐴(1))softmax(A(1)).

import numpy as np

def softmax(X):
    X_exp = np.exp(X)
    partition = X_exp.sum(axis=1, keepdims=True)
    return X_exp / partition  # 这里应用了广播机制。

softmax([[2, 3,4], [3, 5, 7]])

array([[0.09003057, 0.24472847, 0.66524096],
       [0.01587624, 0.11731043, 0.86681333]])

但如果输入值较大或较小时，会出现内存溢出的现象：

softmax([1000, 1000, 100])

C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:5: RuntimeWarning: overflow encountered in exp
C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:7: RuntimeWarning: invalid value encountered in true_divide





array([nan, nan,  0.])

softmax([-10000, -1020, 100, -70220])

array([0., 0., 1., 0.])

一种简单有效避免该问题的方法就是让 exp(𝑧𝑗)exp⁡(zj) 中的 𝑧𝑗zj 替换为 𝑧𝑗−max𝑖{𝑧𝑖}zj−maxi{zi}, 由于 max𝑖maxi 是个固定的常数，所以 exp(𝑧𝑗)exp⁡(zj)的值没有改变。但是，此时避免了溢出现象的出现。

def softmax(X):
    X = np.asanyarray(X)
    X -= X.max(axis=-1, keepdims=True)
    X_exp = np.exp(X)
    print(X_exp)
    partition = X_exp.sum(axis=-1, keepdims=True)
    return X_exp / partition  # 这里应用了广播机制。

softmax([1000, 1000, 100])

[1. 1. 0.]





array([0.5, 0.5, 0. ])

softmax([-10000, -1020, 100, -7220])

[0. 0. 1. 0.]





array([0., 0., 1., 0.])

softmax([-10000, -1020, 100, -70220])

[0. 0. 1. 0.]





array([0., 0., 1., 0.])

当然这种做法也不是最完美的，因为 softmax 函数不可能产生 0 值，但这总比出现 nan 的结果好，并且真实的结果也是非常接近 00 的。

除此之外，还有一个问题：如果我们计算 logsoftmax(𝑧𝑗)log⁡softmax(zj) 时，先计算 softmaxsoftmax 再将其传递给 loglog，会错误的得到 −∞−∞

np.log(softmax([-10000, -1020, 100, -70220]))

[0. 0. 1. 0.]


C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: RuntimeWarning: divide by zero encountered in log
  if __name__ == '__main__':





array([-inf, -inf,   0., -inf])

最简单的处理方式是直接加一个很小的常数：

np.log(softmax([-10000, -1020, 100, -70220])+ 1e-7)

[0. 0. 1. 0.]





array([-1.61180957e+01, -1.61180957e+01,  9.99999951e-08, -1.61180957e+01])

为了解决此数值计算的不稳定，MXNet 提供了：

from mxnet.gluon import loss as gloss
loss = gloss.SoftmaxCrossEntropyLoss()

解决计算交叉熵时出现的数值不稳定的问题。